Тема 4. Переменный электрический ток.
Лекция №12
Цепи синусоидального тока, получение синусоидальной э.д.с.
Соотношения напряжения и тока на идеальных элементах схем замещения.
Резонанс напряжений.
Цепи синусоидального тока, получение синусоидальной э.д.с.
Определение 1.
Цепями синусоидального тока называются такие электрические цепи, в которых электрические величины (электродвижущие силы, напряжения и токи) изменяются во времени по гармоническому (синусоидальному) закону.
Источниками в цепях синусоидального тока являются генераторы переменного тока,
в которых возбуждаются синусоидальные Э.Д.С.
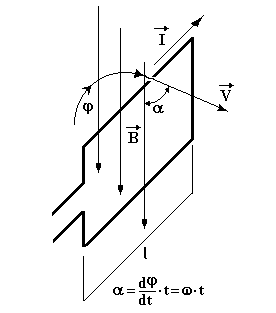Рассмотрим физические аспекты генерирования переменных токов и напряжений.
Соответственно известной схеме с рамкой в магнитном поле, её вращение приводит к возбуждению в ней Э.Д.С. индукции.
Количественно, величина возбуждаемой Э.Д.С., определяется соотношением
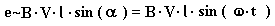
где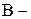 
индукция внешнего магнитного поля, 
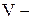линейная скорость вращения контура, 
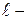длина стороны контура, 
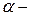угол между векторами скорости и индукции, 
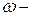угловая скорость вращения, 
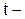текущее время.
Обозначив –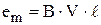 
получаем, что
.
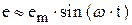Таким образом, в контуре возбуждается синусоидальная э.д.с., которая является причиной появления тока, который, также как и э.д.с., изменяется во времени по гармоническому (синусоидальному) закону.
Соотношения напряжения и тока на идеальных элементах схем замещения.
Рассматривая конкретный идеализированный элемент электрической цепи, будем считать заданным синусоидальный ток и характеристику этого элемента (
).
Поставленная задача будет заключаться в определении напряжения и требуемых количественных и временных соотношений.
|
|
а) Идеальный резистивный элемент R.
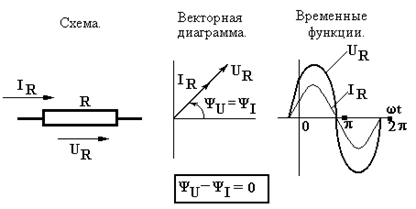
Дано:
По участку цепи с резистором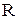 
проходит ток
, где 
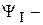начальная фаза тока.
Найти:
Напряжение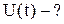 
Решение.
Примечание. Векторные диаграммы используются для наглядности представления расчётных характеристик в цепях переменного тока.
Определение 1.
Совокупность векторов электрических величин, изображённых в общей координатной системе, называется векторной диаграммой.
Используя закон Ома, записываем, что
,
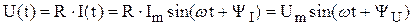где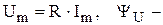 
фаза напряжения, 
.
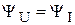Полученный результат говорит о том, что амплитуда напряжения пропорциональна амплитуде тока, начальные фазы равны между собой и фазовый сдвиг (это разность фаз!) между током и напряжением равен нулю.
На рисунках вверху (средний) показана соответствующая векторная диаграмма и временная развёртка тока и напряжения на резисторе (справа).
б) Идеальный индуктивный элемент L.
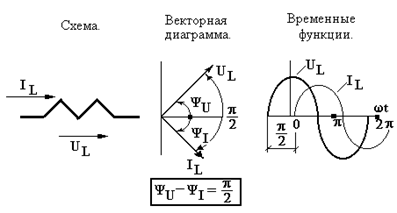
Дано:
По участку цепи с индуктивным элементом 
проходит ток , где 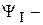начальная фаза тока.
Найти:
Напряжение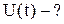
Решение.
При протекании тока, в цепи возбуждается э.д.с. самоиндукции 
.
Согласно второму правилу Кирхгофа с учётом знаков, можно записать, что
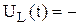εS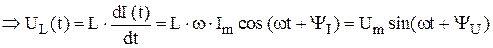 
,
где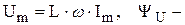 
фаза напряжения, 
.
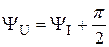По аналогии с законом Ома для резистора в данном случае можно ввести понятие индуктивного сопротивления.
Определение 2.
Коэффициент пропорциональности между амплитудами напряжения и тока, а именно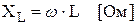 
, называется индуктивным сопротивлением индуктивного элемента.
Тогда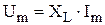 
.
Полученные результаты говорят о том, что амплитуда напря жения пропорциональна амплитуде тока (с коэффициентом пропорциональности, равным индуктивному сопротивлению), а фазовый сдвиг между током и напряжением равен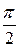 
(напряжение опережает ток на четверть периода!), в отличие от резистивного элемента, где таковой отсутствовал!
|
|
На рисунках вверху (средний) показана соответствующая векторная диаграмма и временная развёртка тока и напряжения на индуктивном элементе (справа).
б) Идеальный ёмкостной элемент С.
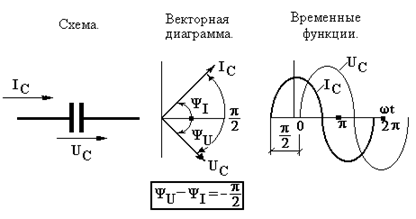
Дано:
По участку цепи с емкостным элементом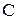 
проходит ток , где 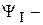начальная фаза тока..
Найти: Напряжение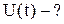
Решение.
Если в цепи протекает ток, то заряд на ёмкости будет равен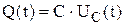 
.
По определению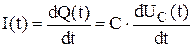 
или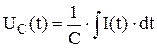 
.
Подставляя под знак интеграла выражение для тока (постоянную интегрирования принимакем равной нулю, так как, физически, постоянная составляющая напряжения на ёмкости отсутствует!), находим, что
,
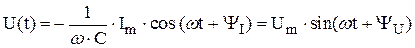где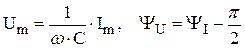 
.
По аналогии с законом Ома для резистора в данном случае можно ввести понятие ёмкостного сопротивления.
Определение 3.
Коэффициент пропорциональности между амплитудами напряжения и тока, а именно 
, называется екостным сопротивлением емкостного элемента.
Тогда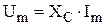 
.
Полученные результаты говорят о том, что амплитуда напряжения пропорциональна амплитуде тока (с коэффициентом пропорциональности, равным емкостному сопротивлению), а фазовый сдвиг между током и напряжением равен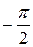 
(ток опережает напряжение по фазе на четверть периода!), в отличие от резистивного элемента, где таковой отсутствовал!
На рисунках (средний) показана соответствующая векторная диаграмма и временная развёртка тока и напряжения на емкостном элементе (справа).
|
|
Примечание. Индуктивное и емкостное сопротивления идеализированных элементов объединяются общим названием РЕАКТИВНЫЕ сопротивления.
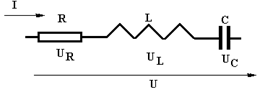
Резонанс напряжений.
Рассмотрим схему из последовательно соеди напряжений нённых идеализированных элементов 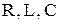, отличительной особенностью которой являетсявозможность явления, называемого резонансом напряжений.
Пусть в цепи протекает синусоидальный ток –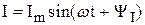 
.
Расчётные соотношения для токов и напряжений на элементах рассматриваемого участка цепи были получены ранее.
Аналогичным образом, можно получить соотношение, связывающее ток и напряжение для всего участка в целом.
Опуская промежуточные выкладки, записываем, что суммарное падение напряжения будет равно
где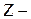 
так называемое, полное сопротивление участка последовательно соединённых идеализированных элементов – 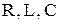, которое определяет пропорциональную связь между модулями напряжения и тока – 
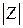, а также сдвиг по фазе между ними – 
.
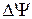Итак,
· модуль полного сопротивления –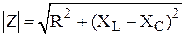 
;
· фазовый сдвиг напряжения относительно тока –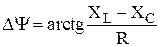 
.
Примечание. Величина суммарного фазового сдвига определяется активным и реактивными сопротивлениями. В зависимости от их величин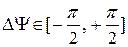 
.
Особенностью рассмотренной схемы, как указано ранее, является возможность возникновения, так называемого, «резонанса напряжений ».
Физически, это явление предполагает равенство амплитуд напряжений на реактивных элементах при противоположной их направленности. В этом случае падение напряжения происходит только на резисторе.
Обратимся к выражениям для модуля полного сопротивления и фазового сдвига..
При резонансе полное сопротивление цепи должно быть минимальным. Это возможно, когда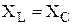 
. В этом случае 
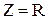, фазовый сдвиг - 
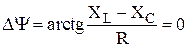, а ток 
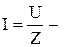максимален.
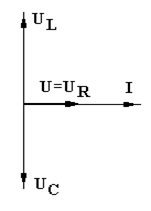Из равенства 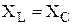следует условие возникновения резонанса в терминах частоты сигнала, а именно,
.
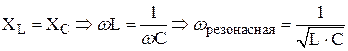Специфическая векторная диаграмма, соответствующая рассматриваемому резонансу напряжений, показана на рисунке слева.