Свойства жидкостей
План
1. Характеристика жидкого состояния. Ближний порядок.
2. Поверхностное натяжение. Силы, возникающие на кривой поверхности. Формула Лапласа. Смачивание и капиллярные явления.
1. Характеристика жидкого состояния. Жидкое состояние, занимает промежуточное положение между газами и кристаллами, сочетает в себе некоторые черты обоих этих состояний. Для кристаллического состояния характерно упорядоченное расположение частиц (атомов или молекул), в газах в этом смысле полный хаос. Согласно рентгенографическим исследованиям, в отношении характера расположения частиц жидкости занимают промежуточное положение.
В расположении частиц жидкости наблюдается так называемый ближний порядок. Это означает, что по отношению к любой частице расположение ближайших к ней соседей является упорядоченным. Однако по мере удаления от данной частицы расположение по отношению к ней других частиц становится всё менее упорядоченным и довольно быстро порядок в расположении частиц полностью исчезает.
В кристаллах имеет место дальний порядок – упорядоченное расположения частиц по отношению к любой частице наблюдается в пределах значительного объёма.
Оценить структуру вещества позволяет радиальная функция распределения (в некоторых учебниках она называется парной функцией распределения). Выберем некоторую молекулу в качестве тела отсчёта. Среднее число молекул в сферическом слое объёмом  , находящихся на расстоянии r от выбранной молекулы (Рис. 10.1) обозначим dN(r). Вероятность обнаружить молекулы в этом сферическом слое
, находящихся на расстоянии r от выбранной молекулы (Рис. 10.1) обозначим dN(r). Вероятность обнаружить молекулы в этом сферическом слое

|  , где N – общее число молекул в некотором рассматриваемом объёме V, g(r) – радиальная функция распределения. В , где N – общее число молекул в некотором рассматриваемом объёме V, g(r) – радиальная функция распределения. В
|
| Рис. 10.1 |
случае идеального газа никакие элементы объёма не имеют преимущества и вероятность нахождения частицы в данном объёме пропорционально объёму и g(r)= 1.
В идеальном кристалле структура жёсткая и все взаимные расстояния являются фиксированными (Рис. 10.2).

| Говорят, что в идеальном газе вообще нет порядка, а в кристалле – дальний порядок – на любом расстоянии от данного атома находится строго определённое количество других атомов, располагающихся друг относительно друга строго определённо. Радиальные функции распределения для кристаллов и идеального газа представлены на рис. 10.3. |
| Рис. 10.2 |
Пики соответствует узлам решётки, а конечная ширина линии g(r) является следствием колебаний атомов относительно узла в реальном кристалле.

| Заметим, что для кристалла  зависит не только от модуля вектора зависит не только от модуля вектора  , но и от его направления. В некотором другом направлении пики могут находится на других расстояниях. Для жидкостей функция , но и от его направления. В некотором другом направлении пики могут находится на других расстояниях. Для жидкостей функция  представлена на рис. 10.4. На малых расстояниях поведение подобно кристаллам (пики чередуются, но представлена на рис. 10.4. На малых расстояниях поведение подобно кристаллам (пики чередуются, но
|
| Рис. 10.3 |
более сглажены, чем у кристалла). На дальних расстояниях кривая  стремится к 1 как для идеального газа.
стремится к 1 как для идеального газа.

| В жидкостях с удлиненными молекулами наблюдается взаимная ориентация молекул в пределах значительного объёма, чем обуславливается анизотропия оптических и некоторых других свойств. Такие жидкости получили название жидких кристаллов. У них |
| Рис. 10.4 |
упорядочена только ориентация, взаимное же расположение, как и в обычных жидкостях, дальнего порядка не обнаруживает.
2. Поверхностное натяжение.
Молекулы жидкости располагаются настолько близко друг к другу, что силы притяжения между ними имеют значительную величину. Взаимодействие быстро убывает с расстоянием, начиная с некоторого расстояния r (радиус молекулярного действия). На каждую молекулу, находящуюся в поверхностном слое толщиной r, будет действовать сила, направленная внутрь жидкости (Рис. 10.5).

| Переход молекулы из глубины жидкости в поверхностный слой связан с необходимостью совершения работы против действующих в поверхностном слое сил. Эта работа (за счёт кинетической энергии молекул) идёт |
| Рис. 10.5 |
на увеличение потенциальной энергии молекулы. То есть в поверхностном слое молекулы обладают дополнительной потенциальной энергией - поверхностной  .
.
Из-за наличия действующих на молекулы в поверхностном слое сил, направленных внутрь жидкости, жидкость стремится к сокращению своей поверхности, как если бы она была заключена в упруго растянутую плёнку, стремящуюся сжаться (никакой плёнки на самом деле нет).
Представим плёнку жидкости (например, мыльную плёнку), натянутую на проволочную рамку, одна из сторон которой (перемычка) может перемещаться (Рис. 10.6). Благодаря стремлению поверхности уменьшиться, на проволочку будет действовать сила. Она направлена по касательной к поверхности жидкости, перпендикулярно к участку контура 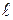 (длина перемычки), на который она действует (
(длина перемычки), на который она действует ( ).
).

| Сила поверхностного натяжения, приходящаяся на единицу длины участка контура 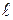 , называется коэффициентом поверхностного натяжения (размерность н/м).
Вследствие стремления поверхностного слоя к сокращению со стороны плёнки будет действовать на перемычку сила, равная , называется коэффициентом поверхностного натяжения (размерность н/м).
Вследствие стремления поверхностного слоя к сокращению со стороны плёнки будет действовать на перемычку сила, равная  . Чтобы перемычка находилась в равновесии, к ней нужно приложить внешнюю силу F, . Чтобы перемычка находилась в равновесии, к ней нужно приложить внешнюю силу F,
|
| Рис. 10.6 |
равную силе натяжения плёнки, т.е.  . Коэффициент 2 появляется из-за того, что плёнка имеет два поверхностных слоя.
. Коэффициент 2 появляется из-за того, что плёнка имеет два поверхностных слоя.
Жидкость вне поля внешних сил будет принимать форму с минимальной поверхностью, т.е. форму шара.
Давление под искривлённой поверхностью.
В случае искривлённой поверхности силы поверхностного натяжения стремятся сократить эту поверхность. (Рис. 10.7).

| Благодаря этим силам в жидкости возникает дополнительное давление  , а давление в жидкости , а давление в жидкости 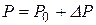 , где , где  - -
|
| Рис. 10.7 |
давление в случае неискривлённой поверхности, причём  >0 в случае выпуклой поверхности, и
>0 в случае выпуклой поверхности, и  <0, если поверхность вогнутая (в этом случае поверхностный слой, стремится сократиться, растягивает жидкость и давление уменьшается).
<0, если поверхность вогнутая (в этом случае поверхностный слой, стремится сократиться, растягивает жидкость и давление уменьшается).
Вычислим дополнительное давление для сферической поверхности жидкости. Рассечём мысленно сферическую каплю жидкости диаметральной плоскостью на два полушария. Из-за поверхностного натяжения

| оба полушария (Рис. 10.8) притягиваются друг к другу с силой:
 .
Эта сила прижимает друг к другу оба полушария по поверхности .
Эта сила прижимает друг к другу оба полушария по поверхности  и обуславливает дополнительное давление: и обуславливает дополнительное давление:
Лаплас обобщил эту формулу на поверхность любой формы. | |
| Рис. 10.8 |
Формула Лапласа выглядит так:

| |||
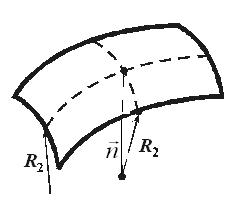
| Где  и и  – радиусы кривизны в двух взаимно перпендикулярных плоскостях, пересечение которых совпадает с нормалью к поверхности жидкости в интересующей нас точке (Рис. 10.9). Например, для поверхности цилиндрической формы один из радиусов кривизны стремится к – радиусы кривизны в двух взаимно перпендикулярных плоскостях, пересечение которых совпадает с нормалью к поверхности жидкости в интересующей нас точке (Рис. 10.9). Например, для поверхности цилиндрической формы один из радиусов кривизны стремится к  и и
 . .
| ||
| Рис. 10.9 | |||
Смачивание и капиллярные явления.
Смачивание – явление, возникающее при соприкосновении жидкости с поверхностью твёрдого тела или другой жидкости. Выражается, в частности, в растекании жидкости по твёрдой поверхности. Смачивание вызывает образование мениска в капиллярной трубке, определяет форму капли на твёрдой поверхности и др. (Заметим, что обычно смачивание рассматривают как результат межмолекурного взаимодействия, однако смачивание может быть результатом химической реакции, диффузионных процессов).
Мерой смачивания обычно служит краевой угол между касательными к поверхности жидкости. (Рис. 10.10). Если 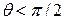 , то говорят, что
, то говорят, что

| жидкость смачивает поверхность твёрдого тела. При 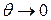 имеет место полное смачивание. Если имеет место полное смачивание. Если  , то жидкость не смачивает поверхность. При , то жидкость не смачивает поверхность. При  мы имеем полное несмачивание. Условие равновесия элемента контура длиной мы имеем полное несмачивание. Условие равновесия элемента контура длиной  (расположен перпендикулярно плоскости рисунка 10.10 в т. А). (расположен перпендикулярно плоскости рисунка 10.10 в т. А).
|
| Рис. 10.10 |
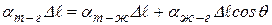 ,
,
где  коэффициенты поверхностного натяжения жидкости на границах: твёрдое тело – газ, твёрдое тело – жидкость, жидкость – газ. Сокращая на
коэффициенты поверхностного натяжения жидкости на границах: твёрдое тело – газ, твёрдое тело – жидкость, жидкость – газ. Сокращая на  , получим для краевого угла соотношение:
, получим для краевого угла соотношение:
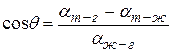
|
(Например, полное смачивание будет при  ).
).
Смачивание имеет важное значение в промышленности. Хорошее смачивание необходимо при крашении, стирке, обработке фотоматериалов, пайке. Примеси сильно сказываются на величине поверхностного натяжения. Например, растворение в воде мыла уменьшает её коэффициент поверхностного натяжения почти в 1,5 раза (что, в частности и обуславливает использование мыла в качестве моющего средства). Несмачивание может приводить к тому, что из решета, нити которого покрыты парафином (при небольшом уровне воды), вода не выливается, опровергая известную поговорку.
Капиллярные явления.
Существование смачивания и краевого угла приводит к тому, что вблизи стенок сосуда наблюдается искривление поверхности жидкости. Если жидкость смачивает стенки, поверхность имеет вогнутую форму, если не смачивает – выпуклую. Такого рода изогнутые поверхности жидкости называются мениском. (рис. 10.11)
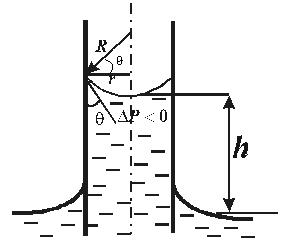
| 
|
| Смачивание | Несмачивание |
| Рис. 10.11 |
Под искривлённой поверхностью в капилляре давление будет отличаться от давления под плоской поверхностью на величину  . Между жидкостью в капилляре и в широком сосуде устанавливается такая разность уровней
. Между жидкостью в капилляре и в широком сосуде устанавливается такая разность уровней  , чтобы гидростатическое давление
, чтобы гидростатическое давление  уравновешивало капиллярное давление
уравновешивало капиллярное давление  . В случае сферической формы мениска
. В случае сферической формы мениска
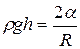 . Радиус кривизны мениска выразим через краевой угол
. Радиус кривизны мениска выразим через краевой угол  и радиус капилляра r
и радиус капилляра r 
 , тогда
, тогда  ,
,
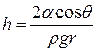
|
В случае смачивания  и высота поднятия жидкости в капилляре
и высота поднятия жидкости в капилляре  тем больше, чем меньше радиус капилляра r.
тем больше, чем меньше радиус капилляра r.
Капиллярное явление занимает в жизни человека исключительную роль. Снабжение влагой растений, деревьев происходит именно с помощью капилляров, которые есть в каждом растении. Капиллярные явления могут играть и отрицательную роль. Например, в строительстве. Необходимость гидроизоляции фундаментов зданий вызвана капиллярными явлениями.
Вопросы для самоконтроля
1.Охарактеризуйте жидкое состояние в сравнении с кристаллами и газами.
2.Что такое дальний и ближний порядок?
3.Что позволяет сделать радиальная функция распределения? Нарисуйте ее для кристаллов, жидкостей и газов.
4.Что такое коэффициент поверхностного натяжения?
5.Как рассчитать дополнительное давление под искривленной поверхностью?
6.Что такое смачивание? Что является мерой смачивания? Приведите примеры процессов, для которых необходимо хорошее смачивание.
7.От чего зависит высота поднятия жидкости в капилляре?
Лекция №5 (11)
Свойства твёрдых тел
План
1. Аморфные и кристаллические тела. Строение и типы кристаллов. Де
фекты в кристаллах.
2. Механические свойства кристаллов. Механизм пластической деформа-
ции. Деформация упругого растяжения. Закон Гука.
Аморфные и кристаллические тела.
В аморфных телах существует ближний порядок расположения атомов. Кристаллы обладают дальним порядком расположения атомов. Аморфные тела изотропны, кристаллические – анизотропны.
При охлаждении и нагревании кривые зависимости температуры от времени различны для аморфных и кристаллических тел. Для аморфных тел переход из жидкого в твёрдое состояние может быть десятки градусов. Для кристаллов температура плавления постоянна. Возможны случаи, когда одно и тоже вещество, в зависимости от условий охлаждения, может быть получено как в кристаллическом, так и в аморфном твёрдом состоянии. Например, стекло при очень медленном охлаждении расплава может кристаллизоваться. При этом на границах мелких образующихся кристаллов будет происходить отражение и рассеяния света, и закристаллизованное стекло теряет прозрачность.
Кристаллическая решётка. Основным свойством кристаллов является регулярность расположения в них атомов. О совокупности точек, в которых расположены атомы (точнее атомные ядра), говорят как о кристаллической решётке, а сами точки называются узлами решётки.
Основной характеристикой кристаллической решётки является пространственная периодичность её структуры: кристалл как бы состоит из повторяющихся частей (ячеек).
Мы можем разбить кристаллическую решётку на совершенно одинаковые параллелепипеды, содержащие одинаковое количество одинаково расположенных атомов. Кристалл представляет собой совокупность параллелепипедов, параллельно сдвинутых по отношению друг к другу. Если сместить кристаллическую решётку параллельно самой себе на расстояние длины ребра, то решётка совместится сама с собой. Эти смещения называются трансляции, а симметрии решётки по отношению к этим смещениям говорят как о трансляционной симметрии (параллельный перенос, поворот относительно оси, зеркальное отражение и т.п.).
Если в вершине какой-либо элементарной ячейки находится атом, то такие же атомы должны, очевидно, находиться и во всех остальных вершинах этой и других ячеек. Совокупность одинаковых и одинаково расположенных атомов называется решёткой Браве данного кристалла. Она представляет как бы скелет кристаллической решётки, олицетворяющий собой всю её трансляционную симметрию, т.е. всю её периодичность.
Классификация различных типов симметрии кристаллов основывается, прежде всего, на классификации различных типов решёток Браве.
Наиболее симметричной решёткой Браве является решётка, имеющая симметрию куба (кубическая система). Существует три различных
| решётки Браве, относящихся к кубической системе: простая | 
| , | |
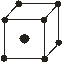
| объемно-центрированная (в центре куба – атом), гранецентрированная (кроме атомов в вершинах – ещё по атому в | ||
центрах всех их граней). Кроме кубической есть тетрагональная, ромбическая, моноклинная и другие (рассматривать не будем).
Решётка Браве, вообще говоря, не включает в себя всех атомов в кристалле. Реальная кристаллическая решётка может быть представлена как совокупность нескольких решёток Браве, вдвинутых одна в другую.
Физические типы кристаллов.
По роду частиц, из которых построена кристаллическая решётка, по характеру сил взаимодействия между ними, различают ионные, атомные, металлические и молекулярные кристаллы.
1. Ионные кристаллы. В узлах кристаллической решётки располагаются попеременно положительные и отрицательные ионы. Эти ионы притягиваются друг к другу электростатическими (кулоновскими) силами. Пример: решётка каменной соли  (рис. 11.1).
(рис. 11.1).

|
| Рис. 11.1 |
2. Атомные кристаллы. Типичными представителями являются графит и алмаз. Связь между атомами – ковалентная. В этом случае каждый из валентных электронов входит в электронную пару, связывающую данный атом с одним из соседей.
3. Металлические кристаллы. Решётки состоят из положительно заряженных ионов, между которыми находятся “свободные” электроны. Эти электроны ”коллективизированы“ и могут рассматриваться как своего рода ”электронный газ“. Электроны играют роль “цемента”, удерживая “+” ионы, иначе решётка распалась бы. Ионы же удерживают электроны в пределах решётки.
4. Молекулярные кристаллы. Примером является лёд. В узлах – молекулы, которые связаны между собой силами Ван-дер-Ваальса, т.е. силами взаимодействия молекулярных электрических диполей.
Могут быть одновременно несколько видов связей (например, в графите – ковалентная, металлическая и Ван-дер-Ваальсовская).
Дефекты в кристаллах.
В реальных кристаллических решётках существует отклонения от идеального расположения атомов в решётках, которые мы до сих пор рассматривали. Все такие отклонения называются дефектами кристаллической решётки.
Точечные дефекты – такие, при которых нарушается ближний порядок:
| 1 – отсутствие атома в каком-либо узле (вакансия) (рис. 11.2); | 
|
| Рис. 11.2 | |
| 2 – замена своего атома “чужими” (рис. 11.3); | 
|
| Рис. 11.3 | |
| 3 – внедрение своего атома или чужого в межузельное пространство (рис. 11.4) | 
|
| Рис. 11.4 |
Другой вид дефектов – дислокации – линейные дефекты кристаллической решётки, нарушающие правильное чередование атомных плоскостей. Они нарушают дальний порядок, искажая всю его структуру. Они играют важную роль в механических свойствах твёрдых тел. Простейшие типы дислокаций краевая и винтовая. В случае краевой дислокации лишняя кристаллическая плоскость вдвинута между соседними слоями атомов (рис. 11.5).
В случае винтовой дислокации часть кристаллической решётки сдвинута относительно другой (рис. 11.6)

| 
| |
| Рис. 11.5 | Рис 11.6 |
