В качестве начального шага при расчете интегралов по формулам (6) – (8), (12), (19) можно рекомендовать число, получаемое по эмпирической формуле 
, где 
– заданная погрешность вычисления, при работе с формулой трапеций 
= 2, при работе с формулой Симпсона 
4.
Для вычисления шага интегрирования можно использовать формулы для оценки остаточного члена и определять шаг из неравенства, например, для формулы трапеций:
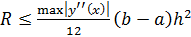, (24)
принимая 
. При этом следует помнить о том, что определяется двумя составляющими: погрешностью усечения и погрешностью округления, которая возникает при вычислении по формуле (24) над приближенными исходными данными. Такой вариант определения шага интегрирования весьма трудоемок: необходимо найти 
для формулы прямоугольника,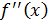 
для формулы трапеций, 
для формулы Симпсона и правила 
, далее найти максимум соответствующей производной на отрезке интегрирования. Такие вычисления технически весьма трудоемки.
На практике вычисления интегралов целесообразно вести с использованием компьютеров, составляя программу на одном из языков высокого уровня. В этом случае выбор шага, удовлетворяющего заданной точности, лучше выполнить автоматически, с использованием приема, который называют двойным пересчетом (правило Рунге). Например, при расчете интеграла по формуле Симпсона с шагом 
= 0,2 получено значение интеграла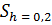 
, затем шаг уменьшается в два раза, т. е. 
, и вычисляется интеграл еще раз: 
, далее сравниваются 
и . Совпадающие десятичные разряды принадлежат точному значению 
, если 
, шаг h уменьшают вдвое и процедуру повторяют, пока разность не станет меньше 
Погрешность формулы Симпсона пропорциональна 
, при увеличении шага в два раза погрешность увеличивается в 16 раз. Для сравнения результатов вычислений следует фактическое отклонение разделить на 16 – 1= 15, т. е. 
, для оценки погрешности по формуле трапеций следует использовать коэффициент 
.
Если подынтегральная функция задана в виде таблицы с постоянным шагом , то оценка погрешности может быть выполнена с использованием формул, устанавливающих связь между соответствующей производной и конечной разностью:
(25)
; (26)
. (27)
Задания
1. 
| 2.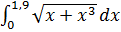 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10.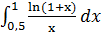 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|
21. 
| 22. 
|
23. 
| 24. 
|
25. 
| 26. 
|
27. 
| 28.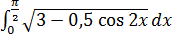 
|
29. 
| 30. 
|
31. 
| 32. 
|
33. 
| 34. 
|
35. 
| 36. 
|
37. 
| 38. 
|
39. 
| 40. 
|
41. 
| 42. 
|
43. 
| 44.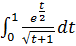 
|
45. 
| 46. 
|
47. 
| 48. 
|
49. 
| 50. 
|
51. 
| 52. 
|
53. 
| 54. 
|
55. 
| 56. 
|
57. 
| 58.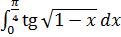 
|
1.7. Контрольные вопросы
1) В чем заключается идея приближенного интегрирования?
2) Запишите формулы метода прямоугольников для приближенного вычисления интегралов.
3) Как уменьшить погрешность в методе прямоугольников?
4) Дана подынтегральная функция 
. Какой из методов вычисления интегралов будет наиболее эффективен?
5) Можно ли методами прямоугольников и трапеций получить точное значение интегралов?
6) Запишите формулу метода трапеций для вычисления определенного интеграла.
7) Назовите известные вам формулы для вычисления определенных интегралов. Какие виды интерполяции в них используются?
8) Запишите формулу Симпсона для вычисления определенных интегралов.
9) В чем состоит метод двойного пересчета (правило Рунге)?
10) Являются ли постоянными весовые коэффициенты, используемые в формуле Ньютона – Котеса?
11) Задана подынтегральная функция 
. Какой из методов даст наиболее точный результат?
12) Что произойдет с погрешностью вычисления интеграла при уменьшении числа отрезков разбиения?
13) Приведите блок-схему метода прямоугольников, отрезок интегрирования разбить на 10 равных частей.
14) Приведите блок-схему метода Симпсона, точность решения 0,001 (использовать правило Рунге).
15) Приведите блок-схему метода трапеций, отрезок интегрирования разбить на 10 равных частей.
16) Составьте программу для метода прямоугольников с использованием правила Рунге.
17) Как оценить погрешность интеграла, вычисленного численным
методом?
18) Можно ли оценить погрешность вычисления интеграла численным методом, если аналитический вид подынтегральной функции неизвестен?
Библиографический список
1.Вержбицкий В. М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения: Учебное пособие/ В.М. Вержбицкий. М.: ОНИКС 21 век, 2013. 382 с.
2. Вержбицкий В. М. Численные методы. Линейная алгебра и нелинейные уравнения: Учебное пособие / В. М. Вержбицкий. М.: ОНИКС 21 век, 2013. 431 с.
Учебное издание
ЕПИФАНЦЕВА Маргарита Ярополковна
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
«ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ»
ПО ДИСЦИПЛИНАМ
«ЧИСЛЕННЫЕ МЕТОДЫ» И «ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА»
 |
Редактор Н. А. Майорова
⃰⃰ ⃰ ⃰
Подписано в печать 11.03.2019. Формат 60 × 84 1/16.
Офсетная печать. Бумага офсетная. Усл. печ. л. 1,2. Уч.-изд. л. 1,4.
Тираж 80 экз. Заказ.
⃰ ⃰
Редакционно-издательский отдел ОмГУПСа
Типография ОмГУПСа
⃰
644046, г. Омск, пр. Маркса, 35
УДК 519.6(075.8)
ББК 22.19я73
Е67
Учебно-методическое пособие к выполнению лабораторной работы «Численное интегрирование» по дисциплинам «Численные методы» и «Вычислительная математика» / М. Я. Епифанцева; Омский гос. университет путей сообщения. Омск, 2019. 18 с.
В учебно-методическом пособии рассмотрены методы прямоугольников, трапеций, Симпсона и обобщающая формула Ньютона – Котеса, предназначенные для вычисления однократных определенных интегралов.
Предназначено для студентов 2-го курса, обучающихся по специаль-ностям «Информационная безопасность автоматизированных систем», «Информационно-аналитические системы безопасности» и по направлению подготовки «Приборостроение».
Библиогр.: 2 назв. Рис. 4.
Рецензенты: канд. техн. наук, доцент Е. В. Толкачева;
канд. физ.-мат. наук, доцент О. В. Гателюк.
© Омский гос. университет
путей сообщения, 2019