М. Я. ЕПИФАНЦЕВА
УЧЕБНО - МЕТОДИЧЕСКОЕ ПОСОБИЕ
К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
«ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ»
ПО ДИСЦИПЛИНАМ
«ЧИСЛЕННЫЕ МЕТОДЫ» И «ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА»
ОМСК 2019
Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Омский государственный университет путей сообщения
_____________________________________
М. Я. Епифанцева
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
«ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ»
ПО ДИСЦИПЛИНАМ
«ЧИСЛЕННЫЕ МЕТОДЫ» И «ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА»
Утверждено методическим советом университета
Омск 2019
ОГЛАВЛЕНИЕ
Введение………………………………………………………………….….. 5
Лабораторная работа. Численное интегрирование……………………….. 6
1. Численные методы вычисления интегралов……………………….….…. 6
1.1. Формулы прямоугольников………………………………….…….. 6
1.2. Формула трапеций………………………………………………….. 8
1.3. Формула Симпсона (парабол)……………………………………… 9
1.4. Формулы Ньютона 
Котеса……………………………………….. 12
1.5. Выбор шага интегрирования………………………………………. 13
1.6. Задания………………………………………………………….…… 14
1.7. Контрольные вопросы……………………………………….……... 16
Библиографический список………………………………………………… 17
ВВЕДЕНИЕ
Для вычисления определенных интегралов используется формула Ньютона – Лейбница
, (1)
где 
– первообразная для 
.
В ряде случаев не удается выразить первообразную через элементарные функции. В некоторых задачах подынтегральная функция задана на отрезке 
в виде таблицы или графика. Такие интегралы можно вычислить только численными методами. Идея численного интегрирования состоит в замене подынтегральной функции 
другой функцией, для которой можно найти первообразную. В качестве такой функции берут либо алгебраический многочлен, либо тригонометрический многочлен и т. д. в зависимости от решаемой задачи.
Численное вычисление однократного интеграла называется механической квадратурой. Соответственно и используемые формулы называют квадратурными. При этой замене полагаем
, (2)
где 
– интерполирующая или аппроксимирующая функция простого вида, 
– погрешность замены подынтегральной функции на функцию простого вида. Если задана аналитически, то можно оценить погрешность формулы (2). 
Вычисление определенного интеграла 
сводится к вычислению площади, ограниченной функцией , осью абсцисс и прямыми 
и 
(рис. 1).
В настоящем пособии представлены краткие теоретические сведения о возможных вариантах вычисления определенных интегралов при постоянном шаге, варианты заданий, контрольные вопросы, необходимые для защиты.
Рис. 1. График подынтегральной функции
Лабораторная работа
Численное интегрирование
Цель работы: вычислить интеграл численными методами с заданной точностью 
.
Порядок выполнения работы
1) Изучить теоретический материал.
2) Получить задание.
3) Составить программу для реализации формул:
а) формулы прямоугольников;
б) формулы трапеций;
в) формулы Симпсона с заданным (использовать правило Рунге);
г) формулы 
.
4) Оформить лабораторную работу.
5) Защитить лабораторную работу (см. контрольные вопросы).
1. Численные методы вычисления интегралов
Формулы прямоугольников
Вычисляем интеграл 
. Полагаем, что непрерывна на отрезке . Определенный интеграл можно вычислить, используя единую формулу на всем отрезке:
или 
(3)
В любом варианте погрешность вычисления велика. Для ее уменьшения принято отрезок делить на части и применять формулу к каждой из его частей.
Вначале создадим сетку по оси 
(рис. 2). Для этого отрезок ра-зобьем на 
равных частей. Шаг сетки вычисляется по формуле:
, (4)
где 
– шаг сетки, тогда 
. Затем на каждом отрезке заменим подынтегральную функцию полиномом нулевой степени 
.
Для вычисления 
воспользуемся ординатой 
, аналогично вычислим 
, 
, 
. Суммарная площадь дает приближенное значение интеграла
. (5)
В общем случае формула при разбиении отрезка 
на равных частей будет иметь вид:
(6)
Рис. 2. График для метода прямоугольников
Это формула левых прямоугольников. Если для вычисления суммарной площади брать правые ординаты, получим формулу правых прямоугольников:
(7)
В методе средних (центральных) прямоугольников в качестве значений ординат берутся значения функции: 
,…. 
.
На рис. 2 они обозначены штриховыми линиями. Получим формулу:
. (8)
Метод прямоугольников имеет существенные погрешности. Для их уменьшения необходимо увеличивать значение – число отрезков разбиения, но в этом случае увеличивается объем вычислительной работы. Метод прямоугольников представлен тремя квадратурными формулами – (6) – (8). Если подынтегральная функция задана аналитически, она достаточно гладкая и можно найти первую и вторую производные от этой функции, то для оценки погрешностей можно использовать следующие формулы:
для формул (6) и (7), (9)
где 
, – отрезок интегрирования; – число отрезков разбиения.
Для формулы (8) погрешность оценивается по уравнению:
(10)
где 
, – отрезок интегрирования; 
– шаг сетки по оси 
; – число отрезков разбиения.
Формула трапеций
Создадим равномерную сетку по оси , . Соединим точки A, B, C, D, E (рис. 3), расположенные на подынтегральной кривой, прямыми линиями, т. е. выполним линейную интерполяцию, тогда площадь каждой трапеции
. (11)
Затем на каждом отрезке заменим подынтегральную функцию полиномом первой степени 
. В общем случае формула трапеций при
разбиении отрезка на n равных частей будет иметь вид (см. рис. 3):
= 
= 
. (12)
Рис. 3. График для формулы трапеций
Очевидно, что погрешность формулы трапеций меньше, чем в формулах прямоугольников. Для уравнения (12) погрешность оценивается по выражению:
, (13)
где 
= 
; b и a – пределы интегрирования; h – шаг сетки; n – число отрезков разбиения.
Формула Симпсона (парабол)
Метод получил название в честь британского математика Томаса Симпсона (1710 – 1761 гг.).
Как и в предыдущих методах, создадим сетку по оси . Разобьем отрезок на 2 равных частей. В этом случае при любом число отрезков будет четным. Аппроксимируем параболой с узлами 
, 
которым соответствуют значения функции (ординаты) 
.
Каждому значению 
соответствует вычисленное значение 
. Произведем квадратичную интерполяцию данной подынтегральной функции на отрезке 
. Для этого заменим на указанном отрезке интерполяционным полиномом Ньютона с узлами 
(рис. 4)
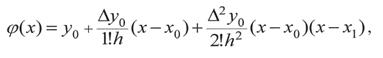
(14)
 |
где где
Заменим 
на 
в выражении (14) и запишем 
Тогда формула (14) будет иметь вид:
(14а)
Вычислим интеграл:
Рис. 4. Аппроксимация параболой
Получим:
(16)
Аналогично найдем интеграл:
(17)
В заключение вычислим интеграл:
(18)
Найдем сумму правых и левых частей выражений (16) – (18):
(19)
Геометрически сущность этого метода заключается в том, что дуга графика подынтегральной функции заменяется параболой, проходящей через точки , далее – 
и т. д. Суммируя парабол, получим обобщенную квадратурную формулу метода парабол (19).
Формула (19) позволяет вычислить интеграл, используя в качестве интерполирующей функции параболу. Выведенную формулу называют формулой Симпсона, или формулой парабол. Этот метод вычисления находит широкое применение на практике. Для оценки погрешности метода, если подынтегральная функция является достаточно гладкой и имеет ограниченную четвертую производную, используется формула:
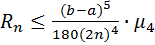, (20)
где 
– число отрезков разбиения. Сравнивая формулы для оценки погрешностей, приведенных методов, видим, что формула метода парабол обеспечивает заданную точность значительно быстрее формулы трапеций. С точки зрения вычислительной работы методы равнозначны.