Занятие №125 – 126.
Тема: Повторение. Уравнения и неравенства.
Цель: Повторить способы решения уравнений и неравенств, подготовка к промежуточной аттестации.
Что повторяем:
1) показательные уравнения и неравенства;
2) логарифмические уравнения и неравенства;
3) тригонометрические уравнения и неравенства.
Теоретический материал для повторения.
Показательными называются уравнения и неравенства, у которых переменная содержится в показатели степени.
Логарифмические уравнения и неравенства — это уравнения и неравенства, в которых переменная величина находится под знаком логарифма.
Тригонометрические уравнения и неравенства – это уравнения, в которых переменная находится под знаком тригонометрической функции.
Решение всех этих уравнений и неравенств мы с вами рассматривали на первом курсе. Наша задача обобщить изученное, привести знания в систему. Начнем с показательных уравнений.
Показательные уравнения
где a>0, a≠1
Если b>0, уравнение имеет один корень: x= 
.
Если b≤0 корней нет.
При решении показательного неравенств, обращаем внимание на основание. Если а>0, знак неравенства сохраняется. Если а<0, знак неравенства меняется.
Логарифмические уравнения
=b, где a>0, a≠1.
Логарифмическое уравнение =b имеет один положительный корень x= 
при любом значении b.
Решая логарифмические неравенства, сравниваем основание логарифма с единицей: если а>1, то знак неравенства сохраняется, а если 0 
знак неравенства меняется.При решении логарифмических неравенств обращаем внимание на область допустимых значений. Затем с учетом ОДЗ и значения решаем неравенство.
Теперь рассмотрим методы решения. Основных приема два: приведение к одинаковому знаменателю и замена переменной.
1 прием. Как в показательном, так и в логарифмическом уравняем основания. Затем сравним показатели или числа, стоящие под знаком логарифма.
2 прием. Замена переменных.
Находим корни и делаем обратную замену. При решении неравенств применяем те же самые приемы.
При решении логарифмических уравнений, возможно появление посторонних корней. Причина их появления — расширение области определения исходного уравнения. Поэтому проверка корней логарифмического уравнения осуществляется либо по области определения, либо непосредственной подстановкой найденных корней в исходное логарифмическое уравнение.
Тригонометрические уравнения – это уравнения вида:cosx=a (-1 
, sinx=a (-1 и tgx=a.
Пример 1. Решить уравнение: 
= 
Решение.
Запишем уравнение в виде(
= 
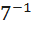, отсюда 2(х-8)=-1,
2х-16 =-1, 2х=16-1, 2х=15, х=7,5.
Ответ: 7,5.
Пример 2. Решить уравнение: 4 
-5 
+ 1=0.
Решение.
Пусть 
у, тогда при подстановке в уравнение вместо 
t, получим 4 
5t +1=0, находим дискриминант D=25-16=9, 
=3, 
= 
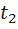отсюда
= 1, х=0 и 
, х=-2.
Ответ: 0; -2.
Пример 3. Решить уравнение:
lg(x+1)+lg(x-1)=lg3
lg(x+1)(x-1)=lg 3
x2-1=3
x2=4, 
2, 
.
При х= -2 выражение lg(x-1) не имеет смысла, т.е. х=-2 посторонний корень.
Можно сначала найти ОДЗ: 
, решая систему, имеем 
из большего берём большее, то есть х 
.
Ответ: 2.
Пример 4. Решить уравнение 
.
Решение.ОДЗ: 5-х 
-х 
, х 
по определению логарифма 5-х= 
, -х=512-5, -х=507,
х=-507 
.
Ответ: -507.
При решении тригонометрических уравнений можно воспользоваться таблицей (упрощённой).
Пример 5. Найдите наименьший положительный корень уравнения tg 
Решение.
= arctg 
+ 
n, делим обе части уравнения на 
и
Умножаем на 3: 2х=1+3k, х=0,5+1,5.
Наименьший положительный корень уравнения получится при k=0,
Х=0,5.
Ответ: 0,5.
Самостоятельно решить уравнение:
1. 
;
2. 
;
3. 2 
x+5cosx=0
Решить неравенство:
1. 
2. 