Сегодня на уроке мы научимся находить условные или, как их ещё называют, относительные экстремумы функций нескольких переменных, и, прежде всего, речь пойдёт, конечно же, об условных экстремумах функций двух и трёх переменных, которые встречаются в подавляющем большинстве тематических задач.
Что нужно знать и уметь на данный момент? Несмотря на то, что эта статья находится «на окраине» темы, для успешного усвоения материала потребуется не так уж и много. На данный момент вы должны ориентироваться в основных поверхностях пространства, уметь находить частные производные (хотя бы на среднем уровне) и, как подсказывает беспощадная логика, разбираться в безусловных экстремумах. Но даже если у вас низкий уровень подготовки, не спешите уходить – все недостающие знания/навыки реально «подобрать по пути», причём безо всяких многочасовых мучений.
Сначала проанализируем само понятие и заодно осуществим экспресс-повторение наиболее распространённых поверхностей. Итак, что же такое условный экстремум? …Логика здесь не менее беспощадна =) Условный экстремум функции – это экстремум в обычном понимании этого слова, который достигается при выполнении определённого условия (или условий).
Представьте произвольную «косую» плоскость в декартовой системе 
. Никакого экстремума здесь нет и в помине. Но это до поры до времени. Рассмотрим эллиптический цилиндр, для простоты – бесконечную круглую «трубу», параллельную оси 
. Очевидно, что эта «труба» «высечет» из нашей плоскости эллипс, в результате чего в верхней его точке будет максимум, а в нижней – минимум. Иными словами, функция, задающая плоскость, достигает экстремумов при условии, что её пересёк данный круговой цилиндр. Именно «при условии»! Другой эллиптический цилиндр, пересекающий эту плоскость, почти наверняка породит иные значения минимума и максимума.
Если не очень понятно, то ситуацию можно смоделировать реально (правда, в обратном порядке): возьмите топор, выйдите на улицу и срубите… нет, Гринпис потом не простит – лучше порежем «болгаркой» водосточную трубу =). Условный минимум и условный максимум будут зависеть от того, на какой высоте и под каким (негоризонтальным) углом осуществлён разрез.
Настало время облачить выкладки в математическое одеяние. Рассмотрим эллиптический параболоид 
, который имеет безусловный минимум в точке 
. Теперь найдём экстремум при условии 
. Данная плоскость параллельна оси , а значит, «высекает» из параболоида параболу. Вершина этой параболы и будет условным минимумом. Причём плоскость не проходит через начало координат, следовательно, точка останется не при делах. Не представили картинку? Срочно идём по ссылкам! Потребуется ещё много-много раз.
Вопрос: как найти этот условный экстремум? Простейший способ решения состоит в том, чтобы из уравнения (которое так и называют – условием или уравнением связи) выразить, например: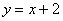 
– и подставить его в функцию:
В результате получена функция одной переменной, задающая параболу, вершина которой «вычисляется» с закрытыми глазами. Найдём критические точки:
– критическая точка.
Далее проще всего использовать второе достаточное условие экстремума:
В частности: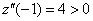 
, значит, функция достигает минимума в точке . Его можно вычислить напрямую: 
, но мы пойдём более академичным путём. Найдём «игрековую» координату:
,
запишем точку условного минимума 
, удостоверимся, что она действительно лежит в плоскости (удовлетворяет уравнению связи):
и вычислим условный минимум функции :
при условии («добавка» обязательна!!!).
Рассмотренный способ без тени сомнения можно использовать на практике, однако, он обладает рядом недостатков. Во-первых, далеко не всегда понятна геометрия задачи, а во-вторых, зачастую бывает невыгодно выражать «икс» либо «игрек» из уравнения связи (если вообще есть возможность что-то выразить). И сейчас мы рассмотрим универсальный метод нахождения условных экстремумов, получивший название метод множителей Лагранжа:
Пример 1
Найти условные экстремумы функции 
при указанном уравнении связи на аргументы 
.
Узнаёте поверхности?;-) …Я рад видеть ваши счастливые лица =)
Кстати из формулировки данной задачи становится ясно, почему условие 
называют уравнением связи – аргументы функции 
связаны дополнительным условием, то есть найденные точки экстремума должны обязательно принадлежать круговому цилиндру.
Решение: на первом шаге нужно представить уравнение связи в виде 
и составить функцию Лагранжа:
, где 
– так называемый множитель Лагранжа.
В нашем случае 
и:
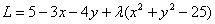
Алгоритм нахождения условных экстремумов весьма похож на схему отыскания «обычных» экстремумов. Найдём частные производные функции Лагранжа, при этом с «лямбдой» следует обращаться, как с константой:
Составим и решим следующую систему:
Клубок распутывается стандартно:
из первого уравнения выразим 
;
из второго уравнения выразим 
.
Подставим 
в уравнение связи и проведём упрощения:
В результате получаем две стационарные точки. Если 
, то:
если 
, то:
Легко видеть, что координаты обеих точек удовлетворяют уравнению 
. Щепетильные люди могут выполнить и полную проверку: для этого нужно подставить 
в первое 
и второе 
уравнения системы, и затем сделать то же самое с набором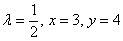 
. Всё должно «сойтись».
Проверим выполнение достаточного условия экстремума для найденных стационарных точек. Я разберу три подхода к решению данного вопроса:
1) Первый способ – это геометрическое обоснование.
Вычислим значения функции 
в стационарных точках:
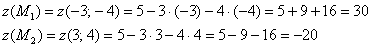
Далее записываем фразу примерно такого содержания: сечение плоскости круговым цилиндром представляет собой эллипс, в верхней вершине которого достигается максимум, а в нижней – минимум. Таким образом, бОльшее значение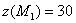 
– есть условный максимум, а меньшее 
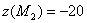– условный минимум.
По возможности лучше применять именно этот метод – он прост, и такое решение засчитывают преподаватели (большим плюсом идёт то, что вы показали понимание геометрического смысла задачи). Однако, как уже отмечалось, далеко не всегда понятно, что с чем и где пересекается, и тогда на помощь приходит аналитическая проверка:
2) Второй способ основан на использовании дифференциала второго порядка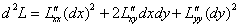 
. Если окажется, что в стационарной точке 
, то функция достигает там максимума, если же 
– то минимума.
Найдём частные производные второго порядка:
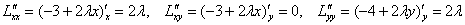
и составим этот дифференциал:
При 
, значит, функция достигает максимума в точке 
;
при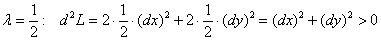 
, значит, функция достигает минимума в точке 
.
Следует отметить, что дифференциал 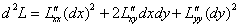представляет собой квадратичную форму относительно 
, и мы получаем быстрый результат, если эта форма определена отрицательно или положительно; причём она может быть таковой даже в «неочевидных» случаях наподобие 
– существует критерий Сильвестра, который позволяет легко установить положительность этого дифференциала.
Но что делать, когда форма знакопеременная, то есть когда знак 
зависит от значений ? Например 
?
В этом случае берём дифференциал от уравнения связи, проведём формальное решение для нашей задачи:
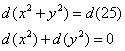
, откуда выражаем, например, 
, и подставляем его в полный дифференциал :
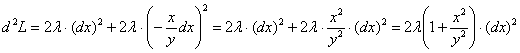, после чего для и точки 
получаем:
;
и для 
:
Гуд.
И, кроме того, можно использовать «тяжёлую артиллерию» – достаточное условие в матричной форме:
3) Продифференцируем по «икс» и по «игрек» уравнение связи:
и составим следующую симметричную матрицу:
Если в стационарной точке 
, то функция достигает там (внимание!) минимума, если 
– то максимума.
Запишем матрицу для значения и соответствующей точки :
Вычислим её определитель:
, таким образом, функция имеет максимум в точке 
.
Аналогично для значения и точки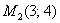 
:
, таким образом, функция имеет минимум в точке .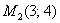
Ответ: при условии :
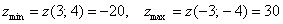
После обстоятельного разбора материала просто не могу не предложить вам пару типовых задач для самопроверки:
Пример 2
Найти условный экстремум функции 
, если её аргументы связаны уравнением 
Пример 3
Найти экстремумы функции 
при условии 
И вновь настоятельно рекомендую разобраться в геометрической сути заданий, особенно, это касается последнего примера, где аналитическая проверка достаточного условия – не подарок. Вспомните, какую линию 2-го порядка задаёт уравнение , и какую поверхность эта линия порождает в пространстве. Проанализируйте, по какой кривой цилиндр пересечёт плоскость и где на этой кривой будет минимум, а где – максимум.
Решения и ответы в конце урока.
Рассматриваемая задача находит широкое применение в различных областях, в частности – далеко ходить не будем, в геометрии. Решим всем понравившуюся задачу о поллитровке (см. Пример 7 статьи Экстремальные задачи ) вторым способом:
Пример 4
Каковы должны быть размеры консервной банки цилиндрической формы, чтобы на изготовления банки пошло наименьшее количество материала, если объем банки равен 
Решение: рассмотрим переменный радиус основания 
, переменную высоту 
и составим функцию площади полной поверхности банки:
(площадь двух крышек + площадь боковой поверхности)
Требуется найти минимум этой функции, при условии, что объём банки равен 
. Таким образом, функция Лагранжа получается прямо из словесной формулировки задачи!
Найдём частные производные по «эр» и по «аш»:
Составим и решим стандартную систему, при этом первое уравнение сразу сокращаем на 
, а второе – на «пи»:
Удобнее начать со второго уравнения:
Нулевой радиус 
не удовлетворяет геометрическому смыслу задачи и поэтому для исследования остаётся 2-й множитель, из которого выражаем:
– подставим в 1-е уравнение:
В результате получаем, что высота оптимальной банки должна быть в 2 раза больше радиуса основания:
Подставим в уравнение связи:
Осталась маленькая проблемка – проверить достаточное условие экстремума. А то вдруг в найденной точке 
функция наоборот – достигает максимального значения?
Возможно, здесь существует лаконичное геометрическое обоснование, но с ходу мне его отыскать не удалось, и поэтому частные производные второго порядка:
Составим полный дифференциал 2-го порядка:
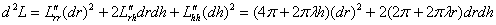
Для нашей критической точки 
:
Легко убедиться, что данная квадратичная форма является знакопеременной, т.е. знак зависит от значений 
и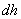 
.
Поэтому находим дифференциал от уравнения связи. В соответствии с правилом дифференцирования произведения:
, откуда выражаем 
– и подставляем в полный дифференциал 2-го порядка:
, значит, функция площади достигает минимума в точке (при заданном объёме консервной банки).
Желающие могут пойти более академичным путём, а именно, продифференцировать по «эр» и по «аш» уравнение связи:
составить симметричную матрицу:
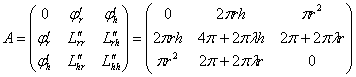
аккуратно подставить в неё 
и вычислить определитель
, с тем же самым выводом об условном минимуме в критической точке.
Если честно, хотел вообще опустить 3-й способ ввиду его трудоёмкости, но мало ли кому понадобится.
Ответ: радиус основания оптимальной банки: 
, её высота: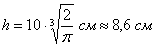 
На практике выбор того или иного пути решения определяется темой, которую вы проходите, и сложностью выбранного метода. Кстати, первый способ (см. Пример 7 статьи Экстремальные задачи ) с технической точки зрения ничуть не приятнее. Также следует отметить, что существует много задач, в которых без метода множителей Лагранжа уже не обойтись, и с таким геометрическим примером мы встретимся в следующем параграфе: