Переключаем внимание на функцию трёх переменных 
, задачи с которой не менее популярны. Принципиальный алгоритм решения остаётся прежним:
Пример 5
Найти условный экстремум функции 
относительно уравнения связи 
Решение: представим уравнение связи в виде 
и составим функцию Лагранжа:
Найдём частные производные 1-го порядка:
Приравниваем частные производные к нулю и присоединяем к системе уравнение связи:
Из первых трёх уравнений выразим:
– подставим в уравнение связи:
– подставим в выражения для «икс», «игрек», «зет»:
Таким образом, стационарная точка: 
Напоминаю, что в целях проверки будет не лишним подставить её координаты и значение 
во все уравнения системы. Здесь это легко сделать устно.
Достаточное условие экстремума. С геометрией дела плохи и поэтому в нашем распоряжении остаются аналитические методы. Составим дифференциал второго порядка функции трёх переменных:
И перед нами не что иное, как квадратичная форма относительно 
.
Если в стационарной точке 
, то функция достигает в ней максимума, если 
– то минимума; если же 
окажется знакопеременным, то потребуются дополнительные действия.
Найдём частные производные 2-го порядка:
Надо сказать, большое везение чего я буду мучиться – даже подставлять ничего не пришлось:
, значит, функция достигает условного минимума в точке 
:
Ответ: при условии :
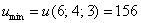
Тренируемся:
Пример 6
Найти условный экстремум функции 
относительно уравнения связи 
Примерный образец чистового оформления задачи в конце урока.
Рассмотренные два примера – это самые что ни есть «заезженные» типовики, но время от времени встречаются и более трудные задания. Первая трудность, состоит, как правило, в решении системы, а вторая – в проверке достаточного условия экстремума. Приглашаю всех ознакомиться с заключительными примерами, которые не только интересны, но и требуют, я бы сказал, творческого подхода:
Пример 7
Найти экстремумы функции 
при условии 
Казалось бы, ничто не предвещает сложностей, и решение начинается как обычно:
Запишем функцию Лагранжа 
и найдём её частные производные 1-го порядка:
Составим стандартную систему:
Привлекательнее всего выглядит 1-е уравнение, из которого, очевидно, рациональнее выразить «лямбду»:
– подставим во второе уравнение:
Примечание: если 
и / или 
, то 
и уравнение связи фактически перестаёт играть таковую роль, поэтому данные случаи исключаем из рассмотрения.
Теперь подставим в третье уравнение:
подставим 
в уравнение связи:
Таким образом: 
На самом деле ещё не очень сложно, бывают куда более «плохие» системы.
Теперь найдём частные производные 2-го порядка:
и аккуратно, ВНИМАТЕЛЬНО составим соответствующий полный дифференциал:
Вычислим значение дифференциала в точке 
:
Используя критерий Сильвестра (да и просто анализируя слагаемые), легко убедиться, что данная квадратичная форма знакопеременна, т.е. знак 
зависит от значений . Поэтому используем уже знакомую схему действий. Найдём дифференциал от уравнения связи, здесь он элементарен:
Теперь нужно выразить какой-нибудь дифференциал, в нашем случае выгоднее 
– подставляем его в наше «знакопеременное недоразумение»:
после чего раскрываем скобки и приводим подобные слагаемые:
В результате получена квадратичная форма уже от двух переменных, запишем её матрицу:
и вычислим угловые миноры:
Таким образом, квадратичная форма определена отрицательно:
, а значит, функция достигает условного максимума в точке 
:
Есть ли другой способ проверки достаточного условия? Есть.
Составляем симметрическую матрицу:
где, 
– частные производные уравнения связи.
Далее рассчитываем угловые миноры 3-го и 4-го порядка в стационарной точке:
Если окажется, что 
, то функция достигает условного минимума в стационарной точке; если 
– то условного максимума.
В нашей задаче: 
,
и для точки получаем следующую матрицу:
Желающие могут провести вычисления, найти 
(рациональнее именно в таком порядке) и сделать тот же самый вывод о наличии условного максимума.
Разумеется, матричный способ более громоздкий, но возможно, кому-то придётся по вкусу.
Ответ: при условии :
Интересно отметить, что в рассмотренном примере нам даже не потребовалось находить значение «лямбда».
Обещанная геометрическая задача:
Пример 8
Определите размеры прямоугольного параллелепипеда (длину, ширину, высоту) максимального объема, если известно, что сумма длин всех его рёбер равна 
.
Постарайтесь не только найти решение, но и добросовестно проверить достаточное условие экстремума.
До сих пор нам встречались задания с единственным уравнением связи, но, вообще говоря, условий может быть несколько: два, три и бОльшее количество. И иногда такие примеры не только существуют в «чистой теории», но и реально встречаются на практике:
Пример 9
Исследовать на экстремум функции 
при условиях 
Здесь функция Лагранжа принимает вид 
и дальнейшие действия будут отличаться мало: находим частные производные 1-го порядка и приравниваем их к нулю, при этом к системе нужно присоединить оба уравнения связи. После нахождения стационарной точки проверяем достаточное условие экстремума, для которого «хватает» дифференциала 2-го порядка.
Решите этот пример самостоятельно – и вы очень удивитесь, как всё легко!
Задача отыскания условных экстремумов реализуема и для функций бОльшего числа переменных, причём условий может быть тоже сколько угодно.