тогда
ρ=4*m / p D2 h,
ε =  . (4)
. (4)
Для полого цилиндра
V =  ph (D2 - d2) Þ ρ= 4 m / p (D2 - d2), (5)
ph (D2 - d2) Þ ρ= 4 m / p (D2 - d2), (5)
где D- внешний диаметр, d- внутренний диаметр, h- высота.
Тогда относительная погрешность определения плотности
ε = 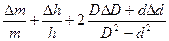 , (6)
, (6)
Для шара
ρ = G * m / pD3,
отсюда
ε=  , (7)
, (7)
Где D-диаметр.
Напомним, что доверительный интервал прямых измерений может быть определён по формуле:
DC = ta,N *  ,
,
где X i- результат отдельного измерения,
N- число измерений величины Х,
ta,N - коэффициент Стьюдента для заданной доверительной вероятности.
III. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
По указанию преподавателя определить плотность тела правильной геометрической формы из числа рассмотренных в предыдущем разделе, руководствуясь следующим примером:
Определение плотности полого цилиндра
1. Ознакомиться с устройством и применением штангенциркуля.
2. Измерить высоту полого цилиндра h, его внешний диаметр D и
внутренний диаметр d. Измерения провести 3 раза, результаты занести в
таблицу. Взвесить цилиндр три раза и значения m массы внести в таблицу.
3. Вычислите средние значения каждой величины, и внести в табл.
4. Вычислите отклонения каждого измеренного значения от среднего и занести в таблицу.
| № измерений | Полый цилиндр | ||||||||||
| m, кг | <m>-mi кг | h, м | <h>-hi, м | D, м | <D>-Di, м | d, м | <d>-di, м | ||||
| 1. | |||||||||||
| 2. | |||||||||||
| 3. | |||||||||||
| Ср. знач | |||||||||||
5. Вычислите среднюю квадратичную погрешность среднего арифметического каждой величины, например: Sh = 
6. Определите доверительный интервал для выполненного числа измерений и степени надёжности a = 0,9 для каждой величины.
7. Запишите окончательный результат для каждой величины. например:
h = <h> ± Dh при a = 0,9.
8. Вычислите относительную погрешность каждого линейного размера и массы.
9. По данным средних значений каждого линейного размера и массы вычислить плотность полого цилиндра по формуле (5).
10. Определить относительную погрешность косвенного измерения плотности по формуле (6).
11. Определить абсолютную погрешность измерения по формуле:
Dρ = ε * <ρ>.
12. Запишите окончательный результат определения плотности
<ρ> ± Dρ при a = 0,9
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Почему результат измерения всегда содержит какую-то погрешность?
2. Какие виды погрешностей вы знаете?
3. Как определяются случайные погрешности косвенных измерений?
4. Как определяется степень надёжности доверительного интервала косвенных измерений?
5. Как изменяется величина доверительного интервала при увеличении (уменьшении) надёжности?
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ:
1. Лабораторные занятия по физике. Под редакцией Л.Л. Гольдина. М.: Наука, 1983.
2. Зайдель А.И. Элементарные оценки ошибок измерений. Л.: Наука, 1974.
3. Майсова Н.Н. Практикум по общему курсу физики. М.: Высшая школа, 1970.
4. Кортнев А.В. практикум по курсу физики. М., 1963.
ЛАБОРАТОРНАЯ РАБОТА № 3
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА
ЦЕЛЬ РАБОТЫ: Знакомство с методом Стокса и экспериментальное определение коэффициента внутреннего трения маловязкой жидкости.
I. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
II.
Реальная жидкость в отличии от идеальной обладает вязкостью (внутренним трением), обусловленной сцеплением между её молекулами. Вязкость проявляется в том, что возникшее в жидкости движение после прекращения действия причин, его вызвавших, постепенно прекращаются. Наблюдаются два вида течения жидкостей. В одном случае жидкость как бы разделяется на слои, которые скользят друг относительно друга, не перемешиваясь. Такое течение называется ламинарным (слоистым).Частицы жидкости в ламинарном потоке не переходят из одного слоя в другой; течение стационарно. При увеличении скорости или поперечных размеров потока характер течения меняется. Возникает перемешивание жидкости, течение становится турбулентным. При турбулентном течении скорость частиц в каждой данной точке всё время изменяется беспорядочным образом- течение не стационарно.
Рейнольдс установил, что характер течения зависит от значения безразмерной величины
Rl = ρ V l / h (3.1.)
где ρ - плотность жидкости;
V - средняя (по сечению трубы) скорость потока;
η - коэффициент вязкости жидкости;
l - характерный для поперечного сечения трубы размер, например, радиус или диаметр при круглом сечении.
Величина (3.1) называется числом Рейнольдса. При малых числах Рейнольдса наблюдается ламинарное течение жидкости. Начиная с некоторого определённого значения Rl кр , называемого критическим, течение приобретает турбулентный характер. Число Рейнольдса может служить критерием подобия для течений жидкостей в трубах, каналах и т. д.
Характер течения различных жидкостей в трубах разных сечений будет совершенно одинаков, если каждому течению соответствует одно и то же сечение Rl.
Пусть в ламинарном потоке скорость течения убывает в направлении Х (рис. 1). Вообразим площадку DS, по которой соприкасаются два соединённых слоя газа. Обозначим через V1 и V2 (скорости течения на расстояниях l ( l - средняя длина свободного пробега молекул) от этой площадки. Пусть V1 > V2. Очевидно, что на хаотическое движение молекул наложится скорость потока V, тогда молекулы верхнего слоя будут обладать большим импульсом, чем молекулы нижнего слоя: mV1 > mV2 (m – масса молекулы). В процессе хаотического движения молекулы внешнего слоя переносят свои импульсы в нижний слой, увеличивая тем самым его скорость. В свою очередь молекулы нижнего слоя переносят свои импульсы в верхний слой, уменьшая его скорость. В результате между слоями возникает внутреннее трение, сила которого будет действовать вдоль площадки DS параллельно скорости потока.
Таким образом, вязкость (или внутреннее трение) обусловлена переносом молекулами из слоя в слой своего импульса (вследствие теплового хаотического движения).
Сила внутреннего трения определяется законом Ньютона:
F=-h 
 S
S 
 (2)
(2)
т.е. сила внутреннего трения, возникающая в плоскости соприкосновения двух скользящих относительно друг друга слоев газа или жидкости, пропорционально площади их соприкосновения и градиенту скорости  .
.
Коэффициент пропорциональности h называется коэффициентом динамической вязкости; он численно равен силе внутреннего трения, действующий на 1 м2 площади соприкосновения параллельно движущихся слоёв при градиенте скорости, равном – 1 с-1.
Наряду с коэффициентом динамической вязкости часто употребляют коэффициент кинематической вязкости
ν = η,
ρ
где ρ - плотность жидкости (газа).
Единицей измерения вязкости в СИ служит такая вязкость, при которой градиент скорости с модулем, равны 1 м/с на 1 м, приводит к возникновению силы внутреннего трения величиной 1 Н на 1 м2 поверхности касания слоёв. Эта единица называется паскаль- секундой
(обозначается Па*с).
Коэффициент вязкости зависит от температуры; у жидкостей коэффициент вязкости сильно уменьшается с повышением температуры.