Комплексные числа
ОПРЕДЕЛЕНИЕ
Комплексные числа – это числа вида z=x+iy, где x, y– действительные числа, i – мнимая единица, удовлетворяющая соотношению i2= -1.
Число x называется действительной частью комплексного числа z 
и имеет обозначение x=Re z.
Число y называется мнимой частью комплексного числа z и имеет обозначение y=Im z.
Например. z= 5 -13 i — комплексное число, действительной частью которого является вещественное число x=Re z=5, а мнимой частью – вещественное число y=Im z=-13.
Если действительная часть комплексного числа равна нулю (x=Re z =0) комплексное число называется чисто мнимым.
Например. z=8 i, где x=Re z=0, y=Im z=8.
Комплексные числа являются расширением действительных (вещественных) чисел. Любое действительное число 
x может быть записано в форме комплексного числа: x+0 i, x-0 i.
Например. Комплексные числа 5+0 i, 5-0 i обозначают действительное число 5.
Равенство комплексных чисел
ОПРЕДЕЛЕНИЕ
Два комплексных числа z1=x1+iy1 и z2=x2+iy2 называются равными, если x1=x2, y1=y2, т.е. равны их действительные и мнимые части.
В противном случае комплексные числа называются неравными.
ПРИМЕР
| Задание | Определить, при каких x и y два комплексных числа z1=x+21 i и z2= -15+y i являются равными. |
| Решение | По определению два комплексных числа являются равными, если равны их действительные и мнимые части, т.е. x=-15, y=21. |
| Ответ | x=-15, y=21. |
Комплексно сопряженные числа
ОПРЕДЕЛЕНИЕ
Сопряженным (или комплексно сопряженным) числом к комплексному числу z=x+iy называется число z=x - iy.
ПРИМЕР
| Задание | Найти для комплексного числа z=- 14 + 56 i его сопряженное число. |
| Решение |  Комплексно сопряженным числом является число вида z=x - iy. Действительной частью комплексного числа является z=- 14 + 56 i число x=Re z=-14, мнимой частью является y=Im z=56.
 Следовательно, сопряженное число имеет вид: z=- 14-56 i.
|
| Ответ |  z=- 14-56 i
|
Противоположные комплексные числа
|
|
ОПРЕДЕЛЕНИЕ
Противоположным к комплексному числу z=x+iy является комплексное число - z=-x-iy.
ПРИМЕР
| Задание | Найти противоположное число к комплексному числу z= 189 - 73 i. |
| Решение | Действительной частью комплексного числа z= 189 - 73 i является число x=Re z=189, мнимой частью – число y=Im z= -73. Следовательно, противоположным числом - z=-x-iy будет являться число -z=-189+73 i. |
| Ответ | -z=-189+73 i. |
Действия над комплексными числами в алгебраической форме.
Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число.
Над комплексными числами в алгебраической форме можно выполнять следующие действия.
Сложение.
Определение. Суммой комплексных чисел z1 = a1 + b1i и z2 = a2 + b2i называется комплексное число z, действительная часть которого равна сумме действительных частей z1 и z2, а мнимая часть - сумме мнимых частей чисел z1 и z2, то есть z = (a1 + a2) + (b1 + b2)i.
Числа z1 и z2 называются слагаемыми.
Сложение комплексных чисел обладает следующими свойствами:
1º. Коммутативность: z1 + z2 = z2 + z1.
2º. Ассоциативность: (z1 + z2) + z3 = z1 + (z2 + z3).
3º. Комплексное число –a –bi называется противоположным комплексному числу z = a + bi. Комплексное число, противоположное комплексному числу z, обозначается -z. Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0
|
|
Пример 1. Выполните сложение (3 – i) + (-1 + 2i).
(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.
2) Вычитание.
Определение. Вычесть из комплексного числа z1 комплексное число z2, значит найти такое комплексное число z, что z + z2 = z1.
Теорема. Разность комплексных чисел существует и притом единственна.
Пример 2. Выполните вычитание (4 – 2i) - (-3 + 2i).
(4 – 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 – 4i.
3) Умножение.
Определение. Произведением комплексных чисел z1=a1+b1i и z2=a2+b2i называется комплексное число z, определяемое равенством: z = (a1a2 – b1b2) + (a1b2 + a2b1)i.
Числа z1 и z2 называются сомножителями.
Умножение комплексных чисел обладает следующими свойствами:
1º. Коммутативность: z1z2 = z2z1.
2º. Ассоциативность: (z1z2)z3 = z1(z2z3)
3º. Дистрибутивность умножения относительно сложения:
(z1 + z2) z3 = z1z3 + z2z3.
4º. z · z = (a + bi)(a – bi) = a2 + b2 - действительное число.
На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.
В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму.
Пример 3. Выполните умножение (2 + 3i) (5 – 7i).
1 способ. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15)i = 31 + i.
2 способ. (2 + 3i) (5 – 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 – 14i + 15i + 21 = 31 + i.
Деление.
Определение. Разделить комплексное число z1 на комплексное число z2, значит найти такое комплексное число z, что z · z2 = z1.
Теорема. Частное комплексных чисел существует и единственно, если z2 ≠ 0 + 0i.
На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю.
|
|
Пусть z1 = a1 + b1i, z2 = a2 + b2i, тогда
.
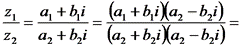
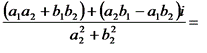
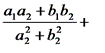
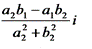В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю.
Пример 4. Найти частное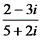 
.
1 способ.
.
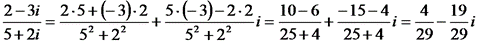2 способ.
.
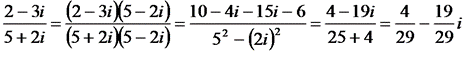Возведение в целую положительную степень.
а) Степени мнимой единицы.
Пользуясь равенством i2 = -1, легко определить любую целую положительную степень мнимой единицы. Имеем:
i3 = i2 i = -i,
i4 = i2 i2 = 1,
i5 = i4 i = i,
i6 = i4 i2 = -1,
i7 = i5 i2 = -i,
i8 = i6 i2 = 1 и т. д.
Это показывает, что значения степени in, где n – целое положительное число, периодически повторяется при увеличении показателя на 4.
Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.
Пример 5. Вычислите: (i 36 + i 17) · i 23.
i 36 = (i 4)9 = 19 = 1,
i 17 = i 4× 4+1 = (i 4)4× i = 1 · i = i.
i 23 = i 4× 5+3 = (i 4)5× i3 = 1 · i3 = - i.
(i 36 + i 17) · i 23 = (1 + i) (- i) = - i + 1= 1 – i.
б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей.
Пример 6. Вычислите: (4 + 2i)3
(4 + 2i)3 = 43 + 3× 42× 2i + 3× 4× (2i)2 + (2i)3 = 64 + 96i – 48 – 8i = 16 + 88i.