Методические указания по дисциплине “Механика грунтов»
для студентов по направлению 08.03.01 «Строительство»
Магнитогорск
Составитель: Р.М.Каримов
Примеры расчет оснований. Физические свойства нескальных грунтов. Определение напряжений в массиве грунта. Расчет осадки оснований; Методические указания по дисциплине "Основания и фундаменты" для студентов специальности по направлению 08.03.01 «Строительство», Магнитогорск: МГТУ, 2016, 28 с.
Рецензент: Андреев В.М.
1. Физические свойства нескальных грунтов
К нескальным грунтам относятся:
- крупнообломочные (несцементированные грунты, содержащие более 50 % по весу частиц с размерами более 2мм (табл. 1.1.));
- песчаные (сыпучие в сухом состоянии грунты, содержащие менее 50 % по весу частиц крупнее 2 мм (табл.1.1.) и не обладающие свойством пластичности (число пластичности Ip < 0,01));
- глинистые (пылевато-глинистые) - связные грунты, для которых число пластичности 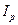 ³ 0,01.
³ 0,01.
Таблица 1.1
Классификация твердых частиц
| Частицы | Размеры частиц, мм | Частицы | Размеры частиц, мм |
| Валунные | > 200 | Песчаные | 2 ÷ 0,05 |
| Галечниковые | 200÷20 | Пылеватые | 0,05 ÷ 0,005 |
| Гравелистые | 20 ÷ 2 | Глинистые | < 0,005 |
Для всех грунтов определяются или вычисляются следующие физические характеристики:
Таблица 1.2
Физические характеристики грунтов
| № п/п | Наименование характеристики | Условное обозначение или формула для вычисления | Единицы измерения | Примечание |
| Характеристики, определяемые из стандартных испытаний | ||||
| 1. | Плотность грунта | 
| т/м3 | |
| 2. | Плотность твер-дых частиц грунта | 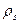
| т/м3 |
Продолжение табл.1.2
| № п/п | Наименование характеристики | Условное обозначение или формула для вычисления | Единицы измерения | Примечание |
| 3. | Природная массовая влажность | 
| ||
| 4. | Влажность грунта на границе текучести |  L L
| Для глинистых грунтов | |
| 5. | Влажность грунта на границе пластичности (раскатывания) |  p p
| ||
| Вычисляемые физические характеристики грунта | ||||
| 6. | Удельный вес грунта | 
| кН/м3 |  = 9,8 м/с2– ускорение свободного падения = 9,8 м/с2– ускорение свободного падения
|
| 7. | Удельный вес твердых частиц грунта | 
| кН/м3 | |
| 8. | Удельный вес скелета грунта | 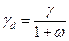
| кН/м3 | |
| 9. | Коэффициент пористости грунта | 
| ||
| 10. | Степень влажности | 
| 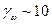 кН/м3- удельный вес воды
кН/м3- удельный вес воды
|
Окончание табл.1.2
| № п/п | Наименование характеристики | Условное обозначение или формула для вычисления | Единицы измерения | Примечание |
| 11. | Удельный вес грунта при учете взвешивающего действия воды | 
| кН/м3 | 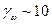 кН/м3 -удель-ный вес воды
кН/м3 -удель-ный вес воды
|
| 12. | Число пластичности | 
| Для глинистых грунтов | |
| 13. | Показатель текучести | 
|
Примечание: в формулы 8 – 10 величина ω подставляется в долях единицы.
1. Плотность грунта  определяется отношением массы образца грунта к его объему.
определяется отношением массы образца грунта к его объему.
2. Плотность грунта 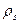 определятся соотношением массы веществ к занимаемому ими объёму.
определятся соотношением массы веществ к занимаемому ими объёму.
3. Природная массовая влажность  - отношение массы воды в объеме грунта к массе этого грунта, высушенного до постоянной массы.
- отношение массы воды в объеме грунта к массе этого грунта, высушенного до постоянной массы.
4. Влажность грунта на границе текучести  L - влажность грунта, при которой грунт находится на границе пластичного и текучего состояний.
L - влажность грунта, при которой грунт находится на границе пластичного и текучего состояний.
5. Влажность грунта на границе пластичности (раскатывания)  p - влажность грунта, при которой грунт находится на границе твердого и пластичного состояний.
p - влажность грунта, при которой грунт находится на границе твердого и пластичного состояний.
Крупнообломочные и песчаные грунты классифицируются:
• в зависимости от крупности частиц – гранулированный состав (табл. 1.3);
• по плотности сложения– e (табл. 1.6);
• по степени влажности - Sr (табл. 1.7).
Таблица 1.3
Классификация грунтов по крупности частиц
| Грунты | Размеры частиц, мм | Содержание частиц по массе, % |
| Крупнообломочные: | ||
| валунные галечниковые гравийные | > 200 > 10 > 2 | > 50 > 50 > 50 |
| Песчаные: | ||
| гравелистые крупные средней крупности мелкие пылеватые | > 2 > 0,5 > 0,25 > 0,1 > 0,1 | > 25 > 50 > 50 ≥ 75 < 75 |
Глинистые грунты классифицируются:
• в зависимости от числа пластичности -  (табл. 1.3);
(табл. 1.3);
• по показателю текучести -  (консистенции, табл. 1.4).
(консистенции, табл. 1.4).
Таблица 1.4
Классификация грунтов по содержанию глинистых частиц
| Грунт | Содержание глинистых частиц по массе, % | Число пластичности 
|
| Глина | > 30 | > 0,17 |
| Суглинок | 30 - 10 | ≤ 0,17 - 0,07 |
| Супесь | 10 - 3 | 0,07- 0,01 |
| Песок | < 3 |
Таблица 1.5
Классификация глинистых грунтов по показателю текучести
| Глинистый грунт | Показатель текучести 
| Глинистый грунт | Показатель текучести 
|
| Супеси: | Суглинки и глины: | ||
| -твердые | 
| -твердые | 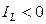
|
| -пластичные | 
| -полутвердые | 
|
| -текучие | 
| -тугопластичные | 
|
| -мягкопластичные | 
| ||
| -текучепластичные | 
| ||
| - текучие | 
|
Для установления наименования грунта после рассева последовательно суммируются проценты содержания частиц различной крупности, начиная с самой крупной фракции.
Задание 1.1. Установить наименование грунта после рассева пробы в зависимости от их крупности согласно табл. 1.6.
Пример
Таблица 1.6
Результаты рассева пробы грунта
| N п/п | Содержание в процентах частиц размером, мм | ||||||
| 2÷0,5 | 0,5.÷0,25 | 0,25÷0,1 | 0,1÷ 0,05 | 0.05÷ 0,01 | 0,01÷0,005 | <0,005 | |
| 1. | 14,9 | 40,2 | 33,9 | 5,9 | 1,5 | 0,7 | 2,9 |
Результаты решения:
1) суммарный состав частиц крупнее 2 мм составляет 0 % - следовательно, песок не гравелистый;
2) суммарный состав частиц крупнее 0,5 мм составляет 14,9 % - следовательно, песок не крупный;
3) суммарный состав частиц крупнее 0,25 мм составляет 55,1%, что более 50 % - следовательно, песок является песком средней крупности.
Задание 1.2. Классифицировать песчаный грунт по плотности сложения согласно табл. 1.7 в зависимости от величины коэффициента пористости  .
.
Задание 1.3. Классифицировать песчаный грунт по степени влажности согласно табл. 1.8 в зависимости от степени влажности Sr грунта.
Таблица 1.7
Классификация песков по плотности в зависимости от значения коэффициентов пористости
| Пески | Значения  для песков для песков
| ||
| плотных | cредней плотности | рыхлых | |
| Гравелистые, крупные, средней крупности |  < 0,55 < 0,55
| 
|  > 0,7 > 0,7
|
| Мелкие |  < 0,6 < 0,6
| 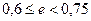
|  > 0,75 > 0,75
|
| Пылеватые |  < 0,6 < 0,6
| 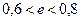
|  > 0,8 > 0,8
|
Таблица 1.8
Классификация грунтов по степени влажности
| Крупнообломочные и песчаные грунты | Степень влажности |
| Маловлажные | Sr  0,5 0,5
|
| Влажные | 
|
| Насыщенные водой | 
|
Задание 1.4. Классифицировать глинистый грунт по числу пластичности 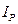 (формула 12 табл. 1.2 и табл. 1.4) и по показателю текучести
(формула 12 табл. 1.2 и табл. 1.4) и по показателю текучести  (табл.1.5).
(табл.1.5).
2. Определение напряжений в массиве грунта
Для оценки несущей способности грунтового основания и прогноза его осадок необходимо уметь определять напряженное состояние в массиве грунта от действия различных внешних нагрузок, приложенных к основанию, и от собственного веса грунта.
При действии вертикальной сосредоточенной силы приложенной к поверхности упругого основания (рис. 2.1.), вертикальные напряжения в точке М определяют по формуле
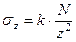 , (2.1)
, (2.1)
где  - безразмерный коэффициент, зависящий от соотношения
- безразмерный коэффициент, зависящий от соотношения  , определяется по таблице 2.1 или по формуле
, определяется по таблице 2.1 или по формуле
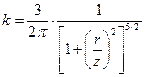 ; (2.2)
; (2.2)
 - величина вертикальной силы;
- величина вертикальной силы;
 ,
,  - соответственно вертикальная и горизонтальная координаты точки
- соответственно вертикальная и горизонтальная координаты точки  .
.
При действии нескольких сосредоточенных сил напряжения в точке  определяют с помощью обычного суммирования по формуле (2.3)
определяют с помощью обычного суммирования по формуле (2.3)
 . (2.3)
. (2.3)

Рис. 2.1. Схема определения напряжений в грунте от сосредоточенной силы (а) и от нескольких сосредоточенных сил (b)
Таблица 2.1
Значения коэффициента 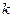

| 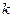
| 
| 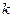
| 
| 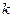
|
| 0,0 | 0,4775 | 0,8 | 0,1386 | 1,6 | 0,0200 |
| 0,1 | 0,4657 | 0,9 | 0,1083 | 1,7 | 0,0160 |
| 0,2 | 0,4329 | 1,0 | 0,0844 | 1,8 | 0,0129 |
| 0,3 | 0,3849 | 1,1 | 0,0658 | 1,9 | 0,0105 |
| 0,4 | 0,3294 | 1,2 | 0,0513 | 2,0 | 0,0085 |
| 0,5 | 0,2733 | 1,3 | 0,0402 | 2,5 | 0,0034 |
| 0,6 | 0,2214 | 1,4 | 0,0317 | 3,0 | 0,0015 |
| 0,7 | 0,1762 | 1,5 | 0,0251 | 4,0 | 0,0004 |
Напряжения, возникающие в грунтах под центром прямоугольной площади загружения равномерно распределенной нагрузкой, находят по формуле
 , (2.4)
, (2.4)
где  - коэффициент рассеивания напряжений, определяемый по табл. 2.2, в зависимости от соотношения
- коэффициент рассеивания напряжений, определяемый по табл. 2.2, в зависимости от соотношения  и
и  (здесь
(здесь 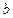 и
и  - соответственно ширина и длина прямоугольника);
- соответственно ширина и длина прямоугольника);
 - равномерно распределенное давление.
- равномерно распределенное давление.
При нахождении  под угловыми точками прямоугольной площади загружения, значения (а не
под угловыми точками прямоугольной площади загружения, значения (а не 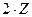 , т. к.
, т. к.  ), также можно принимать по таблице 2.2.
), также можно принимать по таблице 2.2.
Напряжение под угловыми точками определяют по формуле:
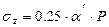 (2.5)
(2.5)
где  - коэффициент рассеивания напряжений, определяемый по табл. 2.2, в зависимости от соотношения
- коэффициент рассеивания напряжений, определяемый по табл. 2.2, в зависимости от соотношения 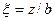 и
и  (здесь
(здесь 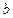 и
и  - соответственно ширина и длина прямоугольника);
- соответственно ширина и длина прямоугольника);
Если проекция рассматриваемой точки  на горизонтальную поверхность полупространства (точка
на горизонтальную поверхность полупространства (точка  ) располагается в пределах площади загружения (рис. 2.1.1), то эту площадь можно разбить на четыре прямоугольника так, чтобы точка
) располагается в пределах площади загружения (рис. 2.1.1), то эту площадь можно разбить на четыре прямоугольника так, чтобы точка  была угловой точкой каждого из них.
была угловой точкой каждого из них.

Рис. 2.1.1 Расчетные схемы к определению напряжений  при действии местного равномерно распределенного давления: а – для точек, расположенных внутри прямоугольной площади загружения; б – под точками, расположенными вне прямоугольной площади загружения
при действии местного равномерно распределенного давления: а – для точек, расположенных внутри прямоугольной площади загружения; б – под точками, расположенными вне прямоугольной площади загружения
Тогда напряжение  найдем суммированием напряжений под угловыми точками четырех площадей загружения:
найдем суммированием напряжений под угловыми точками четырех площадей загружения:
 (2.6)
(2.6)
где  – коэффициенты, принимаемые по таблице в зависимости от отношения сторон площадей загружения I, II, III, IV и отношения
– коэффициенты, принимаемые по таблице в зависимости от отношения сторон площадей загружения I, II, III, IV и отношения  (глубины расположения точки
(глубины расположения точки  ) к ширине каждой из этих площадей.
) к ширине каждой из этих площадей.
Когда проекция точки  на горизонтальную поверхность полупространства (точка
на горизонтальную поверхность полупространства (точка  ) располагается вне пределов площади загружения, точку
) располагается вне пределов площади загружения, точку  аналогично можно представить как угловую точку фиктивных площадей загружения I, II, III, IV. При этом в пределах площадей II и IV фиктивная нагрузка прикладывается в обратном направлении. Напряжение определяется по выражению:
аналогично можно представить как угловую точку фиктивных площадей загружения I, II, III, IV. При этом в пределах площадей II и IV фиктивная нагрузка прикладывается в обратном направлении. Напряжение определяется по выражению:
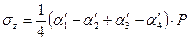 (2.7)
(2.7)
Напряжение в произвольной точке от нагрузки, распределенной по прямоугольной площади, равно алгебраической сумме напряжений в угловых точках прямоугольников, для которых рассматриваемая точка является угловой, при этом алгебраическая сумма площадей этих прямоугольников с учетом знаков в формуле суммирования напряжений должна совпадать с фактической площадью нагрузки.
В естественных условиях, кроме напряжений от внешней нагрузки, прикладываемой к основанию, в каждой конкретной точке основания действуют напряжения от собственного веса вышележащих слоев грунта. Эпюра этих напряжений по глубине однородного грунта имеет вид треугольника. Эпюра вертикальных напряжений от действия собственного веса грунтов неоднородного состава является ломаной линией (рис. 2.2). Вертикальное напряжение в любой точке основания находят по формуле
 , (2.8)
, (2.8)
где  - число слоев грунта, от веса которых определяется напряжение;
- число слоев грунта, от веса которых определяется напряжение;  - удельный вес грунта
- удельный вес грунта  - го слоя;
- го слоя; 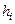 - толщина
- толщина  -го слоя.
-го слоя.
Таблица 2.2
Значения коэффициента 

|  для фундаментов для фундаментов
| ||||||||||
Прямоугольных при 
| Ленточных 
| ||||||||||
| 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.4 | 3.2 | |||||
| 0.0 0.4 0.8 1.2 1.6 2.0 2.4 2.8 3.2 3.6 4.0 4.4 4.8 5.2 5.6 6.0 6.8 7.6 8.4 9.2 | 1.000 0.960 0.800 0.606 0.449 0.336 0.257 0.201 0.160 0.130 0.108 0.091 0.077 0.066 0.058 0.051 0.040 0.032 0.026 0,022 0.019 0.015 | 1.000 0.968 0.830 0.652 0.496 0379 0,294 0.232 0.187 0.153 0.127 0,107 0.092 0.079 0.069 0.060 0.048 0.038 0.032 0.026 0,022 0.018 | 1.000 0.972 0.848 0.682 0.532 0.414 0.325 0.260 0.210 0.173 0.145 0.122 0.105 0.091 0.079 0.070 0.055 0.044 0.037 0,031 0.026 0.020 | 1.000 0.972 0.859 0.703 0.558 0.441 0.352 0.284 0.232 0.192 0.161 0.137 0.118 0.102 0.089 0.078 0.062 0.050 0.042 0.035 0.030 0.024 | 1.000 0.975 0.866 0.717 0.578 0.463 0.374 0.304 0.251 0.209 0.176 0.150 0.130 0.112 0.099 0.087 0.069 0.056 0.046 0.039 0.033 0.026 | 1.000 0.976 0.870 0.727 0.593 0.481 0.392 0.321 0.267 0.224 0.190 0.163 0.141 0.123 0.108 0.095 0.076 0.062 0.051 0.037 0.028 | 1.000 0.976 0.875 0.740 0.612 0.505 0.419 0.350 0.294 0.250 0.214 0.185 0.161 0.141 0.124 0.110 0.088 0.072 0.060 0.051 0.044 0.034 | 1.000 0.977 0.879 0.749 0.630 0.529 0.449 0.383 0.329 0.285 0.248 0.218 0.192 0.170 0.152 0.136 0.110 0.091 0.077 0.065 0.056 0.044 | 1.000 0.977 0.880 0.753 0.636 0.540 0.462 0.400 0.348 0.305 0.270 0.239 0.213 0.191 0.172 0.155 0.128 0.107 0.091 0,078 0.067 0.051 | 1.000 0.977 0.881 0.754 0.639 0.545 0.470 0.410 0.360 0.320 0.285 0.256 0.230 0.208 0.189 0.172 0.144 0.123 0.105 0.091 0.079 0.060 | 1.000 0.977 0.881 0.755 0.642 0.550 0.477 0.420 0.374 0.337 0.306 0.280 0.258 0.239 0.223 0.208 0.184 0.166 0.150 0.137 0.126 0.104 |
Удельный вес водопроницаемого слоя грунта, находящегося ниже уровня грунтовых вод, определяют с учетом взвешивающего действия воды  (см. табл.1.2, строка 11). Если в толще основания имеется водонепроницаемый грунт (глина или суглинок в твердом состоянии), то необходимо учитывать давление столба воды на его кровлю.
(см. табл.1.2, строка 11). Если в толще основания имеется водонепроницаемый грунт (глина или суглинок в твердом состоянии), то необходимо учитывать давление столба воды на его кровлю.
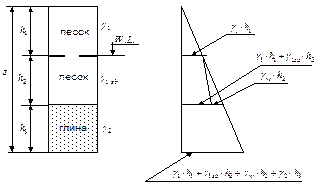 |
Рис. 2.2. Напряжения  от собственного веса грунта (
от собственного веса грунта ( .
. 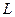 - уровень подземных вод)
- уровень подземных вод)
Задание 2.1. Определить напряжение в точке М от сосредоточенной силы  , приложенной к поверхности грунтового основания. Точка М находится на глубине
, приложенной к поверхности грунтового основания. Точка М находится на глубине 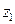 , расстояние от оси силы
, расстояние от оси силы  .
.
Пример:  кН;
кН;  м;
м;  м.
м.
Результаты решения: Определяем отношение  По табл. 2.1 для отношения
По табл. 2.1 для отношения  находим значение коэффициента
находим значение коэффициента  и по формуле (2.1) определяем напряжение
и по формуле (2.1) определяем напряжение
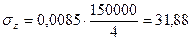 Па.
Па.
Задание 2.2. Определить напряжение в точке М от сосредоточенных сил  ,
, 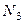 ,
,  приложенных к поверхности грунтового основания. Точка М находится на глубине
приложенных к поверхности грунтового основания. Точка М находится на глубине  . Расстояние от осевых линий приложения сил соответственно
. Расстояние от осевых линий приложения сил соответственно  ,
, 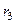 ,
,  . Знак "-" означает что осевая линия силы расположена левее точки М.
. Знак "-" означает что осевая линия силы расположена левее точки М.
Пример: 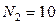 кН;
кН; 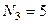 кН;
кН;  кН;
кН;  м;
м;  м;
м; 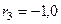 м;
м;  м.
м.
Результаты решения: Находим соотношения  для каждой из трех сил
для каждой из трех сил
 ;
; 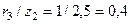 ;
; 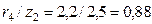
По табл. 2.1 находим значения коэффициентов  для силы
для силы  и
и  для силы
для силы 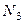 . В табл. 2.1 отсутствует значение коэффициента
. В табл. 2.1 отсутствует значение коэффициента 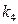 для соотношения
для соотношения 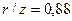 , его значение находим с помощью линейной интерполяции или по формуле (2.2).
, его значение находим с помощью линейной интерполяции или по формуле (2.2). 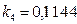 .
.
Имея значения  ,
,  ,
, 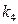 , по формуле (2.3) находим
, по формуле (2.3) находим

 Па.
Па.
Задание 2.3. Построить эпюру распределения напряжений от сосредоточенной силы  с шагом 1 и до глубины 6 м;
с шагом 1 и до глубины 6 м;
а) под точкой приложения силы  ;
;
б) на расстоянии r от точки приложения силы  .
.
Задание 2.4. Определить напряжение в точке М, находящейся на глубине  под центром прямоугольной равномерно распределенной нагрузки интенсивностью
под центром прямоугольной равномерно распределенной нагрузки интенсивностью  , приложенной к поверхности грунтового основания. Размеры фундамента
, приложенной к поверхности грунтового основания. Размеры фундамента  и
и  .
.
Пример: 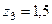 м;
м;  кН/м2;
кН/м2; 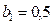 м;
м;  м.
м.
Результаты решения
Находим соотношения: ξ =  , η=0,7/0,5 = 1,4
, η=0,7/0,5 = 1,4
По табл. 2.2 для значений 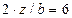 ,
, 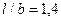 находим коэффициент
находим коэффициент  и вычисляем напряжения по формуле (2.4).
и вычисляем напряжения по формуле (2.4).
 Па.
Па.
Задание 2.5. С шагом  до глубины
до глубины  определить вертикальные напряжения от загруженияпод центром прямоугольной равномерно распределенной нагрузки интенсивностью
определить вертикальные напряжения от загруженияпод центром прямоугольной равномерно распределенной нагрузки интенсивностью  , приложенной к поверхности грунтового основания. Размеры фундамента
, приложенной к поверхности грунтового основания. Размеры фундамента  и
и  .
.
Задание 2.6. Построить эпюры вертикальных напряжений от действия собственного веса грунта в основании для напластований грунтов, показанных на рис. 2.2.
Пример: Схема III;  м;
м;  м;
м;  м;
м;  м;
м;
грунт 1 -глина полутвердая ( кН/м2,
кН/м2,  ,
,  кН/м2);
кН/м2);
грунт 2- супесь ( кН/м2,
кН/м2,  ,
,  кН/м2);
кН/м2);
грунт 3- песок ( кН/м2,
кН/м2,  ,
,  кН/м2).
кН/м2).
Результаты решения: Строим эпюру вертикальных напряжений, используя формулу (2.8). Напряжение на кровле верхнего слоя песка 

Вертикальные напряжения в фунте на уровне грунтовых вод на отметке  м
м
 МПа.
МПа.
Вертикальные напряжения по подошве песка и кровле супеси с учетом взвешивающего действия воды на отметке  м, учитывая, что удельный вес песка с учетом взвешивающего действия воды
м, учитывая, что удельный вес песка с учетом взвешивающего действия воды
 кН/м3,
кН/м3,
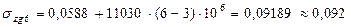 МПа.
МПа.
Удельный вес супеси с учетом взвешивающего действия воды
 кН/м3.
кН/м3.
Напряжение на подошве супеси, находящейся так же во взвешенном состоянии на отметке 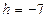 м
м
 МПа.
МПа.
Ниже слоя супеси залегает глина в полутвердом состоянии, являющаяся водоупорный слоем. Следовательно, взвешивающее действие воды в глине проявляться не будет, но на кровлю глины помимо давления от вышележащих слоев грунта добавится гидростатическое напряжение от столба воды, находящегося над слоем глины

Напряжение на кровле глины на отметке 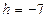 м
м
 МПа.
МПа.
Напряжение по подошве глины на отметке  м
м
 .
.

Строим эпюру вертикальных напряжений, откладывая напряжения в точках, соответствующих границам слоев (рис.2.3).
Рис. 2.3 Расчетная схема и эпюра распределения вертикальных напряжений 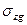 от действия собственного веса грунта по глубине для примера к заданию 2.6
от действия собственного веса грунта по глубине для примера к заданию 2.6