Проекция вектора на ось. Свойства проекций

Векторные и скалярные величины. 2. Линейные операции над векторами

Если некоторая величина вполне определяется ее числовым значением, то ее называют скалярной. Примерами скалярных величин могут служить: масса, плотность, работа, сила тока, температура. Скаляры являются алгебраическими величинами и с ними можно производить любые алгебраические действия: сложение, вычитание, умножение, деление, возведение в степень и т. д.

Направленный отрезок с началом в точке А и концом в точке В называется вектором. Обозначается 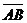или , …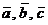

Длина отрезка АВ называется длиной или модулем вектора и обозначается: .

Если точки А и В совпадают, то вектор называется нулевым. Нулевой вектор обозначается либо , либо 0. Нулевой вектор не имеет направления и длина его равна нулю.

Два вектора называются коллинеарными, если они лежат на одной прямой или параллельны одной прямой (лежат на параллельных прямых).

Два вектора называется равными, если они коллинеарны, имеют одинаковое направление и длину.

Произведением вектора на действительное число 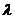называется новый вектор 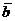, который обладает свойствами:

1^о ;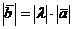

2° направление вектора 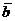совпадает с направлением вектора , если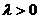
(рис. 2.1, а) и противоположно направлению вектора , если 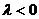(рис. 2.1, б).

Если точка А является началом вектора , то говорят что вектор отложен от точки А. Отложим от точки А вектор 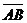, равный . Затем от точки В отложим вектор 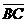, равный . Вектор , равный 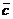, называется суммой векторов и и обозначается:

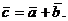
Для любых трех точек А, В, С (рис. 2.2) справедливо равенство (правило треугольника): .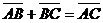

Умножение вектора на число и сложение векторов называются линейными операциями над векторами.

Два вектора называются противоположными, если их длины равны, и они противоположно направлены. Из определения произведения вектора на число следует, что .

Разностью векторов называется вектор 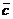, сумма которого с вектором равна вектору . Обозначается: Разность векторов можно определить также равенством: 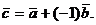Множество всех векторов на плоскости (в пространстве) образуют линейное пространство.

Проекция вектора на ось. Свойства проекций

Осью называется прямая с заданным началом отсчета и направлением (направление на рисунках указывается стрелкой).

Проекцией точки А на ось 0 u называется точка А ₁ пересечения оси и плоскости , перпендикулярной этой оси и проходящей через точку А (рис. 2.3).

Векторной проекцией вектора 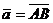на ось 0 u называется вектор 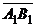, где А ₁, В ₁ – проекции точек А, В на ось 0 u.

Числовой проекцией (или просто проекцией) вектора 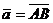на ось 0 u называется число, равное:

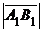, если вектор 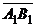и ось 0 u одинаково направлены (рис. 2.4,а);

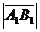– , если вектор и ось 0 u направлены противоположно (рис. 2.4,б);

0, если

Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора

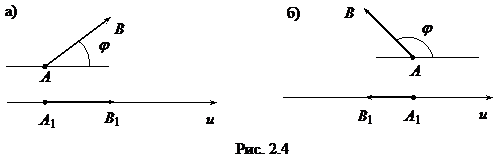
Обозначается проекция вектора на ось 0 u символом: 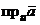. Из определения следует, что

, (2.1)

где 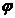– угол между положительным направлением оси 0 u и вектором .

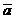Таким образом, если угол 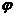острый, то проекция вектора на ось положительна, если 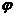тупой угол, то проекция отрицательна; если 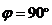, то проекция равна нулю.

Вектор 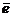называется единичным, если .

Единичный вектор 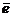, направление которого совпадает с направлением оси 0 u, называется направляющим вектором этой оси или ортом оси. Если 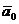– единичный вектор, сонаправленный с вектором , то 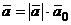, если 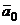направлен противоположно вектору , то .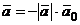

Свойства проекций

1°. Проекция на ось суммы векторов равна сумме проекций этих векторов, т.е.

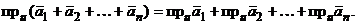(2.2)

2°. Проекция произведения вектора на число равна произведению этого числа на проекцию вектора, т.е.

. (2.3)