Разноуровневые задания
| Уровень 1 | Уровень 2 | Уровень 3 |
Задание 1.
Даны матрицы  и  Найти матрицу  .
Задание 2.
Определить количество решений системы линейных уравнений 
Задание 3.
Даны два вектора:  и  где   угол между векторами равен  . Найти скалярное произведение векторов и 
Задание 4.
Даны точк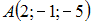и  и  Написать уравнение плоскости, проходящей через точку A перпендикулярно вектору  .
Задание 5.
Найти угловой коэффициент прямой, заданной уравнением  .
Задание 6.
Написать уравнение касательной к графику функции  в точке с абсциссой  .
Задание 7.
Найти предел: 
Задание 8.
Найти производную функции  .
Задание 9.
Найти частную производную  функции  .
Задание 10.
Найти неопределенный интеграл 
Задание 11.
Найти 
Задание 12.
Найти сумму числового ряда  .
Задание 13.
Найти общее решение дифференциального уравнения  .
Задание 14.
Если все возможные значения дискретной случайной величины X увеличились в четыре раза, то ее дисперсия …
Задание 15.
Интервальная оценка математического ожидания нормально распределенного количественного признака X имеет вид. Найти значение a, если выборочная средняя равна 
Задание 16.
Вероятность появления события A в каждом из 200 проведенных испытаний равна 0,4. Оценить с использованием неравенства Чебышева вероятность того, что число X появлений события A будет заключено в пределах от 70 до 90.
| Задание 1.
Составьте такие матрицы А и В, чтобы можно было выполнить над ними операции сложения, вычитания, умножения матриц. Выполните указанные действия.
Задание 2.
Верно ли утверждение, что системы уравнений имеют единственные одинаковые решения:
 ?
Задание 3.
Является ли справедливым утверждение, что если скалярное произведение векторов равно нулю, то хотя бы один из векторов нулевой?
Задание 4.
Является ли прямая, заданная уравнением у = 2х – 4/7, касательной к графику функции y = lnx + ex?
Задание 5.
Написать предел частного многочленов, при нахождении которого используется прием разложения на множители. Найдите предел.
Задание 6.
Написать предел, при нахождении которого используется прием домножения на сопряженное. Найдите предел.
Задание 7.
Написать предел, при нахождении которого используется первый замечательный предел. Найдите предел.
Задание 8.
Написать предел, при нахождении которого используется второй замечательный предел. Найдите предел.
Задание 9.
Написать предел, при нахождении которого используется таблица эквивалентных бесконечно малых. Найдите предел.
Задание 9.
Привести пример функции двух переменных, у которой частные производные равны.
Задание 10.
Составить неопределенный интеграл, при нахождении которого используются следующие свойства интегрирования:
 Найти интеграл.
Задание 11.
Составить неопределенный интеграл, при нахождении которого используется метод замены переменной. Найти интеграл.
Задание 12.
Составить определенный интеграл, при нахождении которого используется метод интегрирования по частям.
Найти интеграл.
Задание 13.
В группе 10 студентов, из которых 6 юношей. Составить случайное, противоположное, невозможное, достоверное события. Найти их вероятность.
Задание 14.
Составить задачу, при решении которой используется геометрическое определение вероятности.
Задание 15.
В группе 10 студентов, из которых 6 юношей. Составить события, образующие полную группу. Найти их вероятность.
Задание 16.
Какие значения может принимать линейный коэффициент корреляции, если уравнение регрессии имеет вид у = 3 – 1,5 х?
| Задание 1. Издержки С (у. е.) при производстве некоторого товара линейно зависят от объема производства Х (ед.). Известно, что при х=2 с=11, а при х=10, с=15. Определить вид функции издержек производства.
Если товар реализуется по цене р=3у. е. за одну ед., то при каком объеме производства прибыль будет нулевой?
Если цена одной ед. продукции равна 4 у. е., то при каких объемах производства предприятие получает прибыль?
Задание 2. Обувная фабрика специализируется по выпуску изделий двух видов: сапог и ботинок. При этом используется сырье двух типов: S1 и S2. Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей: 
Пусть ежедневный объем выпуска сапог и ботинок составляет х1 и х2соответственно. Составить математическую модель для нахождения ежедневного выпуска каждого вида обуви.
Установите соответствие между элементами двух множеств: видом изделия и ежедневным объемом его выпуска.
Стоимость единицы сырья каждого типа задана матрицей-строкой В = (10 15), найти стоимость сырья, затраченного на производство сапог.
Задание 3. Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок. При этом используется сырье трех типов:S1, S2, S3. Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:
Пусть ежедневный объем выпуска сапог, кроссовок и ботинок составляет х1, х2, х3 соответственно. Составить математическую модель для нахождения ежедневного выпуска каждого вида обуви.
Установите соответствие между элементами двух множеств: видом изделия и ежедневным объемом его выпуска.
Стоимость единицы сырья каждого типа задана матрицей-строкой В = (10 20 15). Найти стоимость сырья, затраченного на производство кроссовок.
Задание 4. При производстве некоторого изделия вероятность брака равна 0,2. Составить закон распределения случайной величины X – числа бракованных изделий, если изготовлено три изделия.
Пусть при производстве бракованного изделия предприятие терпит убытки в размере а = 20 тыс. руб., а при производстве небракованного изделия получает прибыль в размере b = 10 тыс. руб. Найти математическое ожидание прибыли предприятия.
При каких значениях а и b ожидаемая прибыль предприятия будет нулевой?
|
назад
Задание по теме «Выборочная совокупность»
1. Записать количественный признак Х, характеризующий студентов группы Г-1 (например, Х – число членов семьи студента группы Г-1, или Х – оценка студента группы Г-1 за последнюю контрольную работу по математике, или Х – масса студента группы Г-1 и т.п.).
2. Провести опрос всех студентов группы по выбранному признаку, результаты оформить в таблицу:
| № п/п | ФИ студента группы Г-1 | Вариант (значение признака) |
3. Построить дискретный или интервальный ряд распределения.
4. Построить графики ряда распределения: полигон (гистограмму), кумуляту, огиву, функцию распределения.
5. Рассчитать средние показатели ряда распределения: среднюю арифметическую, моду, медиану.
6. Рассчитать показатели вариации ряда распределения: размах, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
7. Сделать выводы по результатам исследования, подготовить презентацию.
назад