Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона
Пусть функция y(x), задана таблично в равноотстоящих узлах xi на отрезке [a,b]:
| x | x0 | x1 | x2 | … | xn |
| f(x) | y0 | y1 | y2 | … | yn |
Для нахождения на [a,b] производных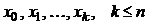 
, 
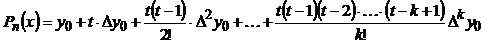и т.д., функцию y приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов 
:
где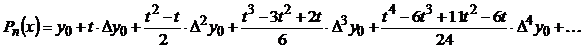 
и 
.
Производя перемножение биномов, получим:
Будем дифференцировать данный многочлен как сложную функцию: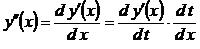 
. Получим:
| (1) |
Так как 
, формула вычисления второй производной будет выглядеть следующим образом:
| (2) |
Таким же способом можно вычислить производные любого порядка.
Чтобы уменьшить погрешность вычисления, при нахождении производных в фиксированной точке х в качестве х0 следует выбирать ближайшее табличное значение аргумента (уменьшить таблицу).
Иногда требуется находить производные функции в основных табличных точках xi. В этом случае формулы численного дифференцирования упрощаются. Так как каждое табличное значение можно считать за начальное, то положим x=x0, следовательно, t=0.
Получим:
| (3) | |
| (4) |
Погрешность приближенного вычисления первой производной в нулевой точке будет равна
Погрешности методов численного дифференцирования
Оценим погрешности методов вычисления. Для разностных правой и левой производных будут справедливы следующие выражения
(5.16)
и
, (5.17)
а для центральной
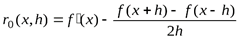. (5.18)
Для оценки погрешностей левых и правых разностных производных первую производную можно получить из разложения в ряд Тейлора в виде
. (5.19)
Здесь и ниже 
и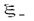 
– некоторые точки, расположенные на интервалах 
и 
соответственно. Откуда погрешности этих методов будут иметь вид
, (5.20)
а оценка абсолютных погрешностей будет удовлетворять неравенству
, (5.21)
где
. (5.22)
Таким образом, формулы (5.2) и (5.3) вычисления правой и левой разностных производных имеют первый порядок точности по 
.
Для центральной разностной производной соответствующие разложения функций 
в ряд Тейлора должны учитывать и производную третьего порядка (вторая производная при вычитании исчезает)
. (5.23)
Отсюда получим
(5.24)
и для оценки абсолютной погрешности будет справедливо неравенство
, (5.25)
где
. (5.26)
Таким образом, производная 
вычисляется при помощи формул центральной разностной производной со вторым порядком точности по , т.е. точнее, чем по формулам (5.2) и (5.3).
Очень часто уменьшение погрешности метода, в данном случае метода численного дифференцирования, сопровождается ростом влияния погрешности исходных данных и вычислительной погрешности. Численное дифференцирование относится именно к таким задачам, которые обычно называют плохо обусловленными.
Оценим совместное влияния погрешностей вычисления и метода для вычисления первой производной. Пусть значение производной вычисляется по формуле (5.3), тогда погрешность метода можно оценить по соотношению (5.21). Если значения функции 
известны с некоторой погрешностью 
(
), то погрешность вычисления 
будет содержать дополнительное слагаемое
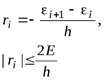, (5.27)
Пренебрегая для простоты погрешностью округления, имеем оценку погрешности в следующем виде
. (5.28)
Из формулы (5.28) очевидно, что уменьшение 
не приводит к увеличению точности вычисления производной, так как возрастает ошибка, связанная с погрешностью определения функции (рисунок 5.1). Погрешности 
возникают вследствие ошибок измерения или предыдущего вычисления по приближенным формулам. Из соотношения (5.28) можно найти оптимальное значение разбиения, находя экстремум правой части, такое 
будет равно
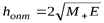. (5.29)
Отметим, что повышение точности метода лишь отчасти повышает точность вычисления производной.
Рисунок 5.1. Зависимость погрешности вычисления первой производной от величины шага.
Задания.
Упражнение 1 Вычислить с одинарной точностью производные g1(x), g2(x) и погрешности d1(x), d2(x) для различных значений x и шага h. Функции f(x) = sin 100x?
Упражнение 2 Что происходит с результатами вычислений в окрестности точек x = 0, π/2, π,...? Как вы это объясните?