Если на основании выборочных данных дается оценка того или иного параметра генеральной совокупности, то при этом необходимо иметь в виду, что данная оценка является лишь приближенным значением неизвестного параметра. При малом объеме выборки значение точечной оценки может очень сильно отклоняться от истинного значения параметра. Вопрос состоит в том, как велико это отклонение.
Чтобы решить этот вопрос, используются интервальные оценки, которые даются в виде доверительного интервала.
Доверительный интервал – это интервал  со случайными границами, в котором с заданной вероятностью
со случайными границами, в котором с заданной вероятностью  находится значение параметра генеральной совокупности.
находится значение параметра генеральной совокупности.
 называется доверительной вероятностью, она характеризует надежность результатов. Чем выше
называется доверительной вероятностью, она характеризует надежность результатов. Чем выше  , тем выше надежность, но при этом снижается точность. В медицинских и биологических исследованиях в качестве
, тем выше надежность, но при этом снижается точность. В медицинских и биологических исследованиях в качестве  берут 0,9; 0,95 или 0,99.
берут 0,9; 0,95 или 0,99.
Доверительный интервал может быть построен для различных числовых характеристик генеральной совокупности. Мы рассмотрим построение доверительного интервала для генеральной средней в том случае, когда исследуемая величина распределена по нормальному закону.
Доверительный интервал для оценки генеральной средней  с заданной доверительной вероятностью
с заданной доверительной вероятностью  нормально распределенного признака Х при неизвестном среднем квадратическом отклонении
нормально распределенного признака Х при неизвестном среднем квадратическом отклонении  (что в основном и имеет место на практике) находится по формуле
(что в основном и имеет место на практике) находится по формуле

где  - вычисленная по выборке выборочная средняя,
- вычисленная по выборке выборочная средняя,
 - квадратный корень из исправленной выборочной дисперсии,
- квадратный корень из исправленной выборочной дисперсии,
 - объем выборки,
- объем выборки,
 - коэффициент Стьюдента, вычисляемый по таблице. Он зависит от доверительной вероятности
- коэффициент Стьюдента, вычисляемый по таблице. Он зависит от доверительной вероятности  и числа степеней свободы
и числа степеней свободы 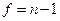 .
.
Величина  , равная половине длины доверительного интервала, представляет собой наибольшее отклонение выборочной средней
, равная половине длины доверительного интервала, представляет собой наибольшее отклонение выборочной средней  от генеральной средней
от генеральной средней  , которое возможно при заданной доверительной вероятности g. Она называется предельной ошибкой выборки.
, которое возможно при заданной доверительной вероятности g. Она называется предельной ошибкой выборки.
Пример. Из большой партии таблеток некоторого лекарственного препарата случайным образом были извлечены 8 таблеток. При измерении массы таблеток были получены следующие результаты (в мг): 151, 147, 152, 152, 151, 148, 151, 148. Оценить истинную массу таблетки с помощью доверительного интервала с доверительной вероятностью  .
.
Решение. Составим дискретный ряд распределения:

| ||||

|
Найдем выборочную среднюю  :
:
 .
.
Для вычисления выборочной дисперсии в данном случае удобнее использовать формулу
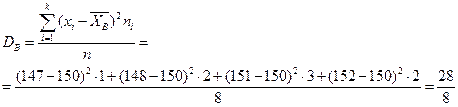 , тогда исправленная выборочная дисперсия будет равна
, тогда исправленная выборочная дисперсия будет равна

и, следовательно, стандартное отклонение равно:
 .
.
По таблице значений коэффициента Стьюдента при доверительной вероятности  и числе степеней свободы
и числе степеней свободы  находим значение
находим значение  .
.
Находим доверительный интервал для оценки истинной массы таблетки:


 .
.
Таким образом, истинное значение массы таблетки с доверительной вероятностью 0,95 заключено в интервале  .
.
Таблица значений коэффициента Стьюдента
| Число степеней свободы f | Доверительная вероятность g | Число степеней свободы f | Доверительная вероятность g | |||||
| 0.95 | 0.99 | 0.999 | 0.95 | 0.99 | 0.999 | |||
| 12.706 | 63.657 | 636.619 | 2.103 | 2.878 | 3.922 | |||
| 4.303 | 9.925 | 31.598 | 2.093 | 2.861 | 3.883 | |||
| 3.182 | 5.841 | 12.941 | 2.086 | 2.845 | 3.850 | |||
| 2.776 | 4.604 | 8.610 | 2.080 | 2.831 | 3.819 | |||
| 2.571 | 4.032 | 6.859 | 2.074 | 2.819 | 3.792 | |||
| 2.447 | 3.707 | 5.959 | 2.069 | 2.807 | 3.767 | |||
| 2.365 | 3.499 | 5.405 | 2.064 | 2.797 | 3.745 | |||
| 2.306 | 3.355 | 5.041 | 2.060 | 2.787 | 3.725 | |||
| 2.262 | 3.250 | 4.781 | 2.056 | 2.779 | 3.707 | |||
| 2.228 | 3.169 | 4.587 | 2.052 | 2.771 | 3.690 | |||
| 2.201 | 3.106 | 4.487 | 2.048 | 2.763 | 3.674 | |||
| 2.179 | 3.055 | 4.318 | 2.045 | 2.756 | 3.659 | |||
| 2.160 | 3.012 | 4.221 | 2.042 | 2.750 | 3.646 | |||
| 2.145 | 2.977 | 4.140 | 2.021 | 2.704 | 3.551 | |||
| 2.131 | 2.947 | 4.073 | 2.000 | 2.660 | 3.460 | |||
| 2.120 | 2.921 | 4.015 | 1.980 | 2.617 | 3.374 | |||
| 2.110 | 2.898 | 3.965 | ¥ | 1.960 | 2.576 | 3.291 |