Точность моделей статики может оцениваться величиной одного из приведенных ниже показателей:
Для вычисления 
на объекте (системы) проводится актив-
ный или пассивный эксперимент, заключающийся в регистрации к различных значений входных переменных системы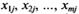 
и соответствующих им установившихся выходных переменных 
Желательно, чтобы переменные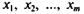 
варьировались во
всем диапазоне, допустимом технологическим регламентом эксплуатации объекта. Переменные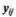 
вычисляются по статической модели при заданных входных переменных системы 
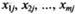Весовые множители 
вводятся для создания возможности сравнения разнородных переменных при неравноточности измерения выходных переменных системы. Чем больше погрешность измерения 
, тем меньше выбирается множитель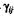 
Если величины 
существенно отличаются друг от друга, то появляется необходимость нормирования отдельных слагаемых в выражении для 
. В этом случае множители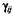 
выполняют роль нормирующих коэффициентов. В частности, при 
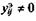их можно принять пропорциональными величинам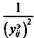 
Для возможности сравнения критериев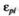 
между собой их величины также целесообразно нормировать путем деления на значение yfj, при котором достигается максимум данного 
. При «достаточно больших» значениях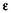 
или 
ММ считается неадекватной реальной системе. В этом случае требуется уточнение структуры математического описания или отдельных «сомнительных» параметров модели. Эта операция может осуществляться постановкой дополнительных лабораторных опытов или применением экспериментально-аналитического метода (последнее возможно, если речь идет о существующей системе).
Вопрос о том, при каком «критическом» значении 
или 
считать ММ адекватной системе, а при каком требовать уточнения уравнений модели, является исключительно сложным и, вероятно, не имеет однозначного ответа. Выбор такого «критического» значения критерия тесно связан с целевым назначением модели, а также с представительностью выборки 
. В частном случае, когда 
— независимые случайные величины, для оценки случайного характера рассогласования между величинами 
и 
могут быть использованы статистические критерии значимости и согласия. Однако и при таком подходе сохраняется субъективный выбор некоторых параметров (вероятностей), от которого зависит ответ на поставленный вопрос о близости 
и 
Чаще всего используют инженерный подход, когда максимальное рассогласование между 
и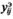 
не должно превышать ошибки измерения экспериментальных данных 
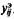, т. е. для оценки точности ММ применяется следующий показатель:
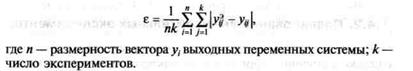
Сопоставляя вычисленный показатель точности ММ с точностью системы контроля, можно сделать вывод об адекватности ММ.
Точность описания динамики системы с сосредоточенными параметрами (координатами) может характеризоваться величинами функционалов:
-
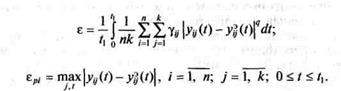
Для получения экспериментальных динамических характеристик системы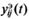 
на объекте проводятся опыты с различными наборами входных переменных (возмущающих сигналов) 
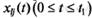. Зависимости 
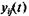есть решения уравнений динамики системы при 
и 
. Показатель степени q обычно принимается равным единице или двум.
Множители 
выбираются иногда из условия выравнивания погрешностей при неравноточных измерениях величин 
. В тех случаях, когда 
существенно различаются между собой по мо-
дулю, множители 
выполняют роль нормирующих коэффициентов (нормирующих функций). Чаще всего 
полагают равными
величинам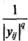 
при 
Значения функционалов е, epi количественно характеризуют степень близости решений уравнений динамики и экспериментально измеренных переходных процессов в реальной системе.
Лекция 6