Переменный электрический ток.
Переменным называется ток, который с течением времени изменяет свою величину или направление.
В промышленности наибольшее распространение получил синусоидальный переменный ток, то есть ток, величина которого изменяется со временем по закону синуса или косинуса:
i =Im*cos(wt+j0) (1)
где Im- амплитуда тока, F=(w t+j0) - фаза колебаний, j0 - начальная фаза.

Цепь переменного тока с омическим сопротивлением. Соединим последовательно активное сопротивление R, катушку индуктивностью L и конденсатор электроемкостью С. Напряжение U, приложенное к данной цепи, распределяется на трех сопротивлениях - активном R, индуктивном XL и емкостном Хс.
Омическое(активное) сопротивление - это сопротивление цепи постоянному току вызывающее безвозвратные потери энергии постоянного тока.
Единственной причиной вызывающей потери постоянного тока является противодействие материала проводника. На преодоление этого противодействия затрачивается часть энергии постоянного тока, которая превращается в тепловую энергию нагревающую проводник. Эта часть энергии обратно в проводник в виде энергии постоянного тока не возвращается.
На резисторах написана величина их омического сопротивления, т. е. сопротивления постоянному току.
Величина омического сопротивления не зависит от величины тока.
I = U/r.
Как следует из последнего выражения, вид закона Ома для цепи переменного тока, содержащей сопротивление r, тот же, что для цепи постоянного тока. Кроме того, из закона Ома видна пропорциональность между мгновенным значением напряжения и мгновенным значением тока. Отсюда следует, что в цепи переменного тока, содержащей сопротивление r, напряжение и ток совпадают по фазе. На рис. 135 даны кривые напряжения и тока и векторная диаграмма для рассматриваемой цепи, причем длины векторов обозначают действующие значения напряжения и тока.

Рис. 135. Графики и векторная диаграмма для цепи переменного тока, содержащей активное сопротивление
Сопротивление проводников переменному току несколько больше их сопротивления постоянному току* (см. § 65). Поэтому сопротивление проводников переменному току называют активным в отличие от сопротивления, которое оказал бы этот проводник при постоянном токе. Обозначается оно также буквой r.
* (Это объясняется тем, что при переменном токе наблюдается неравномерное распределение тока по сечению проводника, так что плотность тока будет возрастать от оси к поверхности проводника. Это явление называется поверхностным эффектом. Неравномерная плотность тока приводит к увеличению сопротивления проводника. Однако при стандартной частоте 50 гц, небольшом сечении и медных или алюминиевых проводах явление поверхностного эффекта сказывается слабо. При высокой частоте, большем сечении и стальных проводах оно значительно.)
Цепь переменного тока с индуктивностью. Рассмотрим цепь (рис. 4.6), в которой к катушке индуктивности L, не обладающей активным сопротивлением (R = 0), приложено синусоидальное напряжение (4.6). 
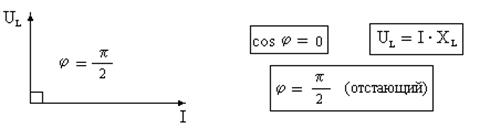
Рис. 16. Векторная диаграмма для идеального индуктивного сопротивления

Рис.17. Векторная диаграмма реального индуктивного сопротивления

Рис. 19. Векторная диаграмма идеального емкостного сопротивления
Реальные конденсаторы также имеют внутреннее активное сопротивление. Поэтому их можно представить как последовательное соединение идеального конденсатора и внутреннего активного сопротивления (рис.20):

Рис.20. Векторная диаграмма реального емкостного сопротивления
Протекающий через катушку переменный ток создает в ней ЭДС самоиндукции  , которая в соответствии с правилом Ленца направлена таким образом, что препятствует изменению тока. Другими словами, ЭДС самоиндукции направлена навстречу приложенному напряжению. Тогда в соответствии со вторым правилом Кирхгофа можно записать:
, которая в соответствии с правилом Ленца направлена таким образом, что препятствует изменению тока. Другими словами, ЭДС самоиндукции направлена навстречу приложенному напряжению. Тогда в соответствии со вторым правилом Кирхгофа можно записать:
 (4.9)
(4.9)
Согласно закону Фарадея ЭДС самоиндукции
 (4.10)
(4.10)
Подставив (4.10) в (4.9), получим:

Решение этого дифференциального уравнения имеет вид:
 (4.12), где
(4.12), где  (4.13)
(4.13)
Деля обе части равенства (4.13) на  , получим для действующих значений
, получим для действующих значений
 (4.14)
(4.14)
Соотношение (4.14) представляет собой закон Ома для цепи с идеальной индуктивностью, а величина  называется индуктивным сопротивлением. Индуктивное сопротивление измеряется в омах.
называется индуктивным сопротивлением. Индуктивное сопротивление измеряется в омах.
Мгновенная мощность в цепи с чисто индуктивным сопротивлением равна:
 (4.15)
(4.15)
Положительные значения мощности соответствуют потреблению энергии катушкой, а отрицательные - возврату запасенной энергии обратно источнику. Средняя за период мощность равна нулю. Следовательно, цепь с индуктивностью мощности не потребляет - это чисто реактивная нагрузка. В этой цепи происходит лишь перекачивание электрической энергии от источника в катушку и обратно. Индуктивное сопротивление является реактивным сопротивлением.
Цепь переменного тока с емкостью Рассмотрим электрическую цепь, в которой переменное напряжение (4.6) приложено к емкости С.
Мгновенное значение тока в цепи с емкостью равно скорости изменения заряда на обкладках конденсатора:
 ; но поскольку q = СU, то
; но поскольку q = СU, то
 , где
, где  (4.25)
(4.25)
Мы видим, что в этой цепи ток опережает напряжение на 2. Переходя в формуле (4.25) к действующим значениям переменного тока 
 ), получим:
), получим:  (4.26)
(4.26)
Это закон Ома для цепи переменного тока с емкостью, а величина  — называется емкостным сопротивлением. Векторная диаграмма для этой цепи показана на рис. 4.12, а временная – на рис. 4.13
— называется емкостным сопротивлением. Векторная диаграмма для этой цепи показана на рис. 4.12, а временная – на рис. 4.13
Мгновенная мощность в цепи, содержащей емкость:
 (4.27)
(4.27) 
Мы видим, что мгновенная мощность изменяется с удвоенной частотой (рис. 4.13). При этом положительные значения мощности соответствуют заряду конденсатора, а отрицательные - его разряду и возврату запасенной энергии в источник. Средняя за период мощность здесь равна нулю, поскольку в цепи с конденсатором активная мощность не потребляется, а происходит обмен электрической энергией между конденсатором и источником. Следовательно, конденсатор так же, как и индуктивность, является реактивным сопротивлением. 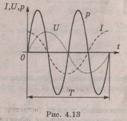
В общем случае ток и напряжение достигают своих максимальных значений не одновременно. При этом говорят, что имеет место разность фаз тока и напряжения (сдвиг по фазе).
Разностью фаз тока и напряжения называется доля периода, на которую одна функция опережает другую (или отстает от нее).
При этом если ток по фазе отстает от напряжения, разность фаз считается положительной (φ >0), в противном случае разность фаз считается отрицательной (φ<0). Нередко разность фаз измеряют не в долях периода, а в угловых градусах. При этом полный период соответствует 3600. В примере, приведенном на рис.2.1, ток опережает напряжение, значит, φ <0.
φ = -  °
°
Приведенный пример определяет метод измерения разности фаз: измерив по шкале на экране осциллографа  и Т, разность фаз можно определить по формуле:
и Т, разность фаз можно определить по формуле:
φ =  (2.10)
(2.10)
Разность фаз напряжения и тока
Условимся под разностью фаз j напряжения и тока всегда понимать разность начальных фаз напряжения  и тока
и тока 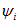 (а не наоборот):
(а не наоборот):

Поэтому на векторной диаграмме угол j отсчитывается в направлении от вектора I к вектору U (рис. 3.10).

Именно при таком определении разности фаз угол j равен аргументу комплексного сопротивления. Угол j положителен при отстающем токе (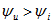 ) и отрицателен при опережающем токе (
) и отрицателен при опережающем токе ( ).
).
Разность фаз между напряжением и током зависит от соотношения индуктивного и емкостного сопротивлений. При 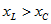 имеем
имеем 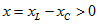 и ток отстает по фазе от напряжения,
и ток отстает по фазе от напряжения,  . При
. При  имеем
имеем  , ток совпадает по фазе с напряжением, rLC -цепь в целом проявляет себя как активное сопротивление. Это случай так называемого резонанса в последовательном контуре. Наконец, при
, ток совпадает по фазе с напряжением, rLC -цепь в целом проявляет себя как активное сопротивление. Это случай так называемого резонанса в последовательном контуре. Наконец, при 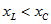 имеем
имеем  , ток опережает по фазе напряжение.
, ток опережает по фазе напряжение.

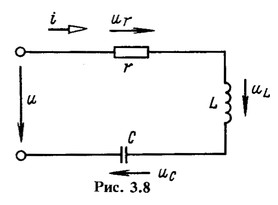
Векторные диаграммы для трех возможных соотношений 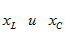 даны на рис. 3.11. При построении этих диаграмм начальная фаза тока
даны на рис. 3.11. При построении этих диаграмм начальная фаза тока  ; принята равной нулю. Поэтому
; принята равной нулю. Поэтому  равны друг другу.
равны друг другу.
Рассматривая при заданной частоте цепь по рис. 3.8 в целом как пассивный двухполюсник, можно ее представить одной из трех эквивалентных схем: при 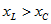 как последовательное соединение сопротивления и индуктивности (
как последовательное соединение сопротивления и индуктивности ( ), при
), при  как сопротивление r и при
как сопротивление r и при  как последовательное соединение сопротивления и емкости (
как последовательное соединение сопротивления и емкости ( ). При заданных L и С соотношение между
). При заданных L и С соотношение между 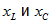 зависит от частоты, а потому от частоты зависит и вид эквивалентной схемы.
зависит от частоты, а потому от частоты зависит и вид эквивалентной схемы.
Выше, в разделе, было принято, что задан ток, а определялись напряжения на элементах и на входных выводах цепи. Однако часто бывает задано напряжение на выводах, а ищется ток. Решение такой задачи не представляет труда. Записав по заданным величинам комплексное напряжение U и комплексное сопротивление Z, определим комплексный ток

и тем самым действующий ток и начальную фазу тока.
Часто равной нулю принимается начальная фаза заданного напряжения:  . В этом случае, как следует из раздела, начальная фаза тока
. В этом случае, как следует из раздела, начальная фаза тока  ; равна и противоположна по знаку разности фаз j, т. е
; равна и противоположна по знаку разности фаз j, т. е  .
.
Установленные выше соотношения между амплитудами и действующими токами и напряжениями, а также выражение для сдвига фаз ф позволяют вычислить ток и не прибегая к записи закона Ома в комплексной форме. Подробно этот путь решения показан в примере 3.4.
Полное сопротивление в цепи переменного тока (Z).
| Содержание | Величина | Наименование |
Обычно цепь переменного тока включает в себя и активное сопротивление, и емкость, и индуктивность. Полное сопротивление (Z) - это векторная сумма всех сопротивлений: активного, емкостного и индуктивного.  - полное сопротивление цепи. Здесь: - полное сопротивление цепи. Здесь:  - активное сопротивление. - активное сопротивление.  - емкостное сопротивление. - емкостное сопротивление.  - индуктивное сопротивление. - индуктивное сопротивление. 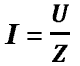 - полное сопротивление определяет силу тока в цепи по закону Ома. - полное сопротивление определяет силу тока в цепи по закону Ома.
| I - действующее значение силы тока | А |
| U - действующее значение напряжения | В | |
| XL - индуктивное сопротивление | Ом | |
| ω - циклическая частота переменного тока | рад/с | |
| L - индуктивность | Гн | |
| C - емкость | Ф | |
| XC - индуктивное сопротивление | Ом | |
| Z - полное сопротивление | Ом | |
| R - активное сопротивление | Ом | |
| ρ - удельное сопротивление проводника | Ом м | |
| l - длина проводника | м | |
| S - площадь сечения проводника | м2 |