Изотермы температурного поля предельного состояния нужно построить для:
t=1500; 1300; 1100; 900; 700; 500; 300; 100.
Для того, чтобы найти координаты точек, лежащих в температурном поле предельного состояния на изотерме T=const, необходимо на графике изохрон распределения температуры (рис.1), выражающих зависимость T=T(y0) при t=const, провести прямую постоянной температуры T=const, параллельную оси абсцисс. Абсциссы точек пересечения горизонтальной прямой постоянной температуры с изохронами распределения температур дают расстояния y0, на которых мгновенная температура равна заданной температуре T=const в соответствующие моменты времени t.
По рис. 1 находим все необходимые точки и заносим их в таблицу №2.
Таблица №2
| 1500ºС | 1300ºС | 1100ºС | 900ºС | 700ºС | 500ºС | 300ºС | 100ºС | ||||||||
| t,сек | y0,мм | t,сек | y0,мм | t,сек | y0,мм | t,сек | y0,мм | t,сек | y0,мм | t,сек | y0,мм | t,сек | y0,мм | t,сек | y0,мм |
Определяем расстояние, пройденное источником нагрева за время t,
Рис. 2
Распределение максимальных температур
Подставляя значения выбранного режима в уравнение максимальных температур для быстродвижущегося линейного источника в тонкой пластине, получим
 |
Таблица №3
| y0, см | 0,3 | 0,5 | 1,0 | 1,5 | 2,0 | 3,0 | 4,0 | 5,0 |
| Тm(y0), ºC |
по результатам расчета, приведенным ниже, построена кривая распределения максимальных температур (рис.1).
Кривая распределения максимальных температур (изображенная пунктиром) является огибающей изохрон, т.е. кривых мгновенного распределения температуры (изображенных сплошными линиями).
Уравнение геометрического места точек с максимальными температурами в координатах XY находим из условия максимума температуры при сварке листов встык, подставляя числовые данные, получим
 | |||
 | |||
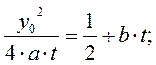Полученные данные сводим в таблицу №4
Таблица №4
| t, сек | ||||||||
| y0, см |
По результатам расчета, приведенным в таблице №4, построена кривая максимальных температур в подвижном температурном поле XOY рис.2.
Эту кривую можно построить и графически. Для этого к каждой изотерме температурного поля проводим касательные, параллельные оси OX. Точки касания соединяем плавной кривой, которая представляет геометрическое место точек с максимальными температурами на поверхности листов XOY.
Термический цикл в точке А
Для расчета изменения температуры в точке А, находящейся на расстоянии y0=…см от оси шва, в уравнение распространения тепла при выбранном режиме сварки листов подставляем расстояние y0 точки А
 |
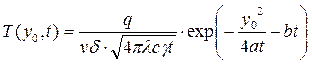По результатам расчета, приведенным в таблице №5, построена кривая изменения температуры в точке А в зависимости от времени, прошедшего после пересечения центром дуги поперечного сечения, в котором находится точка А (рис. 3).
| t, сек | |||||||||
| Т, ºС |
Рис. 3. Кривая изменения температуры в точке А в зависимости от времени
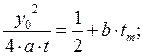Время tm наступления максимальной температуры в точке А, равной 500ºС определяется из условия максимума температуры
 |
откуда
 |
за это время центр дуги успеет удалится от сечения, в котором находиться точка А, на расстояние
-х=…см
Список использованной литературы
1. Введение в сварочные технологии: учебное пособие. /С.Н. Козловский/ –СПб.: Издательство «Лань», 2011. – 416 с.: ил. – (Учебники для вузов. Специальная литература).
2. Основы технологии сварки: учебное пособие. /С.А. Федосов, И.Э. Оськин/ – М.: Машиностроение, 2011. – 125 с.
3. Теория сварочных процессов: Учебник для вузов / А.В. Коновалов, А.С. Куркин, Э.Л. Неровный, Б.Ф. Якушин; Под ред. В.М. Неровного. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2007.
4. Теория сварочных процессов: Учеб. для вузов по спец. “Оборуд. и технология сварочн. пр-ва”/В.Н. Волченко, В.М.Винокуров и др.; Под ред. В.В. Фролова. – М.: Высш. шк., 1988. – 559 с.: ил.
5. Петров Г.Л., Тумарев А.С. Теория сварочных процессов (с основами физической химии). Учебник для вузов. Изд. 2-е, перераб. М., “Высшая школа”, 1977. – 392 с. с ил.
6. Н.Н. Рыкалин «Расчеты тепловых процессов при сварке», государственное научно-техническое издательство машиностроительной литературы, Москва, 1951 г.
7. Линевег Ф. Измерение температур в технике. Справочник. Пер. с нем. 1980. – 544 с.