Те, у кого в четверти «шаткая» оценка по математике между 2 и 3 (то есть рекомендуемый балл в журнале от 2,30 до 2,60) или между 3 и 4 (то есть рекомендуемый балл в журнале от 3,30 до 3,60), могут по желанию в среду 22.12.2021 на восьмом уроке сдать зачёт по теории и получить одну или несколько оценок (не больше трёх), улучшив таким образом четвертную.
Зачёт будет проходить в следующем виде: учащийся вытягивает случайным образом тему (или несколько), отвечает устно по данной теме теорию и показывает её понимание на нескольких примерах. Вытянутую тему можно поменять с оценкой на балл ниже.
Кратко вся теория по главе 2 учебника (по которой и будет проходить зачёт) собрана в «Итогах главы» после §18. В каждом параграфе нужная теория выделена жирным шрифтом или курсивом.
Список вопросов и ориентировочные задания (примеры):
1. Основное свойство дроби (§7)
Вопросы: В чём состоит основное свойство дроби?
Задание: Какие из данных равенств не верны и почему: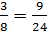 
; 
; 
?
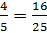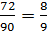2. Сокращение дробей (§8)
Вопросы: Что называют сокращением дробей? Какую дробь называют несократимой? На какое число надо сократить дробь, чтобы получилась несократимая дробь?
Задание: Какие из данных дробей 
; 
; 
; 
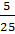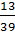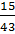несократимы? Сократите дробь 
.
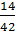3. Приведение дробей к общему знаменателю. Сравнение дробей (§9)
Вопросы: Как привести две дроби к наименьшему общему знаменателю? Как сравнить две дроби с разными знаменателями?
Задание: Приведите дроби к наименьшему общему знаменателю и сравните:
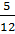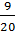и 
; 
и 
.
2. Сложение и вычитание дробей (§10)
Вопросы: Сформулируйте правило сложения и вычитания дробей с разными знаменателями.
Задание: Несколько примеров на вычисление в одно действие, аналогично примерам из №268, 275, 277, 278 или 280 (нумерация по старому учебнику).
|
|
4. Умножение дробей (§11)
Вопросы: Как умножить дробь на натуральное число? Как найти произведение двух дробей?
Задание: Несколько примеров на вычисление в одно действие, аналогично примерам из №333, 335 или 337 (нумерация по старому учебнику).
5. Свойства умножения (§11)
Вопросы: Перечислите свойства умножения (название и свойство в буквенном виде).
Задание: Несколько примеров на упрощение выражений, аналогично примерам из №357 или 359 (нумерация по старому учебнику). В каждом примере указать используемое свойство.
6. Нахождение дроби от числа (§12)
Вопросы: Как найти дробь от числа? Как найти процент от числа?
Задание: 1-3 задачи в одно действие, аналогично №393, 395, 398 или 402 (нумерация по старому учебнику).
7. Взаимно обратные числа (§13)
Вопросы: Какие числа называют взаимно обратными? Для любого ли числа существует обратное ему?
Задание: Несколько примеров на нахождение обратных, аналогично примерам из №435 или 436 (нумерация по старому учебнику); вопросы по ним.
8. Деление дробей (§14)
Вопросы: Сформулируйте правило деления дробей.
Задание: Несколько примеров на вычисление в одно действие, аналогично примерам из №446 или 448 (нумерация по старому учебнику).
9. Нахождение числа по заданному значению его дроби (§15)
Вопросы: Как число по значению его дроби? Как найти число по его процентам?
Задание: 1-3 задачи в одно действие, аналогично №504, 506 или 508 (нумерация по старому учебнику).
10. Преобразование обыкновенной дроби в десятичную. Бесконечные периодические десятичные дроби. (§16-17)
|
|
Вопросы: Как преобразовать обыкновенную дробь в десятичную? (2 способа) В каком случае несократимую дробь можно преобразовать в конечную десятичную дробь?
Задание: Несколько примеров на понимание и вычисление, аналогично заданиям из №540, 542, 550 или 553 (нумерация по старому учебнику).
11. Десятичное приближение обыкновенной дроби. (§18)
Вопросы: Как найти десятичное приближение обыкновенной дроби до нужного разряда?
Задание: Несколько примеров на вычисление, аналогично заданиям из №561 или 563 (нумерация по старому учебнику).