Стационарные временные ряды и их характеристики. Автокорреляционная функция.

Временные ряды. Модели стационарных и нестационарных временных рядов, их идентификация.

1.Общие сведения о временных рядах и задачах их анализа.

Под временным рядом (динамическим рядом, или рядом дина­мики) в экономике подразумевается последовательность наблю­дений некоторого признака (случайной величины) Y в последо­вательные моменты времени. Отдельные наблюдения называются уровнями ряда, которые будем обозначать y_t (t = 1,2,..., п)_, где п — число уровней.

В табл. 1 приведены данные, отражающие спрос на неко­торый товар за восьмилетний период (усл. ед), т. е. временной ряд спроса y_t.

Таблица 1

В качестве примера на рис.1 временной ряд y_t изображен графически.

В общем виде при исследовании экономического временно­го ряда y_t выделяются несколько составляющих:

y_t=u_t+ v_t +c_t+ _{t (t=1,2,…,n),}

_где u_t- тренд, плавно меняющаяся компонента, описывающая чистое влияние долговременных факторов, т. е. длительную («вековую») тенденцию изменения признака (например, рост населения, экономическое развитие, изменение структуры по­требления и т. п.);

v_t — сезонная компонента, отражающая повторяемость эконо­мических процессов в течение не очень длительного периода (го­да, иногда месяца, недели и т. д., например, объем продаж това­ров или перевозок пассажиров в различные времена года);

c_t — циклическая компонента, отражающая повторяемость экономических процессов в течение длительных периодов (на­пример, влияние волн экономической активности Кондратьева, демографических «ям», циклов солнечной активности и т. п.);

_t - случайная компонента, отражающая влияние не поддаю­щихся учету и регистрации случайных факторов.

Рис 1

Следует обратить внимание на то, что в отличие от е, первые три составляющие (компоненты) u_t, v_t,c_t являются закономерны­ми, неслучайными.

Важнейшей классической задачей при исследовании экономиче­ских временных рядов является выявление и статистическая оценка основной тенденции развития изучаемого процесса и отклонений от нее.

Отметим основные этапы анализа временных рядов:

графическое представление и описание поведения вре­менного ряда;

выделение и удаление закономерных (неслучайных) со­ставляющих временного ряда (тренда, сезонных и цикли­ческих составляющих);

сглаживание и фильтрация (удаление низко- или высокочастотных составляющих временного ряда);

исследование случайной составляющей временного ряда, построение и проверка адекватности математической мо­дели для ее описания;

прогнозирование развития изучаемого процесса на осно­ве имеющегося временного ряда;

исследование взаимосвязи между различными времен­ными рядами.

Стационарные временные ряды и их характеристики. Автокорреляционная функция.

Важное значение в анализе временных рядов имеют ста­ционарные временные ряды, вероятностные свойства которых не изменяются во времени. Стационарные временные ря­ды применяются, в частности, при описании случайных состав­ляющих анализируемых рядов.

Временной ряд называется строго стационарным, если совместное распределение вероятностей n наблюдений такое же, как и n наблюдений при любых . Свойства строго стационарных рядов не зависят от момента 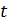: и закон распределения, и его числовые характеристики не зависят от 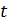. Следовательно, математическое ожидание 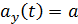, с квадратичным отклонением могут быть оценены по наблюдениям по формулам

,

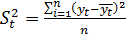
Степень тесноты связи между последовательностями наблюдений временного ряда и может быть определена с помощью коэффициента корреляции :

Так коэффициент измеряет корреляцию между членами одного и того же ряда, его называют коэффициентом автокорреляции, а зависимость - автокорреляционной функцией. (В силу стационарности временного ряда , автокорреляционная функция зависит только от лага , причем . При изучении можно ограничиться только положительных значений ).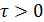

Статистической оценкой является выборочный коэффициент корреляции :

Замечание: С увеличением число пар 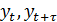– 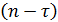уменьшается, поэтому лаг должен быть таким, чтобы число 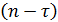было достаточным для определения .

Для стационарных временных рядов с увеличением лага взаимосвязь членов временного ряда и ослабевает и должен убывать по абсолютной величине. В то же время для при небольшом числе пар наблюдений , свойство монотонного убывания при росте τ может нарушаться.

Наряду с автокорреляционной функцией при исследовании стационарных временных рядов рассматривается частная автокорреляционная функция , где - частный коэффициент автокорреляции, то есть коэффициент корреляции между и при устранении влияния промежуточных членов.

Статистической оценкой является выборочная частная автокорреляционная функция , где , - выборочный частный коэффициент корреляции. Выборочный частный коэффициент автокорреляции 1 порядка между членами временного ряда и может быть вычислен по формуле:

,

(где – выборочные коэффициенты автокорреляции между и , 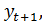и , и , соответственно.

Рассмотрим пример №1,№2.

Замечание. Знание выборочных автокорреляционных функций и может оказать существенную помощь при подборе и идентификации модели анализируемого временного ряда и статистической оценке его параметров.

Отсутствие корреляции между соседними членами служит хорошим основанием считать, что корреляция отсутствует в целом, и обычный метод наименьших квадратов дает адекватные и эффективные результаты.

Рассмотрим два способа обнаружения автокорреляции остатков (а следовательно, и случайных составляющих).

Первый способ – графический. С помощью метода наименьших квадратов оценивается регрессия. Рассчитываются остатки . Строится график зависимости остатков от номера наблюдения – t .

Второй способ – основан на применении критерия Дарбина-Уотсона. Тест Дарбина-Уотсона определяет наличие автокорреляции между соседними членами. Если корреляция ошибок регрессии не равна нулю, то она присутствует и в остатках регрессии , получающихся в результате применения обычного метода наименьших квадратов.

В тесте Дарбина-Уотсона для оценки корреляции используется статистика вида . Для вычислений рекомендуется пользоваться формулой .

Критерий Дарбина-Уотсона не является статистическим, так как распределение статистики зависит не только от числа наблюдений, но и от значений факторов (регрессоров). Поэтому нельзя указать критическую область, которая позволяла бы отвергнуть гипотезу об отсутствии корреляции, если бы оказалось, что в эту область попало наблюдаемое значение статистики . Однако существуют два пороговых значения 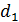и , зависящие только от числа наблюдений, числа регрессоров и уровня значимости, такие, что выполняются условия:

1). Если 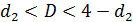, то принимается гипотеза об отсутствии автокорреляции.

2). Если , или 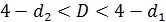, то вопрос о присутствии автокорреляции открыт (зоны неопределенности).

3). Если , то принимается гипотеза о положительной автокорреляции.

4). Если , то принимается гипотеза об отрицательной автокорреляции.