ВКЛАДЫ.
Рассмотрим проблему вкладов в банки на конкретной ситуации. Допустим, мы собираемся покупать квартиру. Пусть это будет хорошая качественная квартира за 10 миллионов рублей. При этом также предположим, что мы устроились на более-менее нормальную работу и зарабатываем по 100 тысяч рублей в месяц. В этом случае за год мы сможем отложить примерно 1 миллион рублей. Разумеется, зарабатывая по 100 тысяч рублей в месяц, за год у нас получится чуть большая сумма — 1200000 — но эти 200000 пусть будут потрачены на еду, на одежду и на прочие ежедневные бытовые радости. Итого, вводные данные таковы: необходимо заработать 10 миллионов рублей, у нас же в распоряжении имеется лишь 1 миллион рублей в год. Возникает естественный вопрос: сколько лет нам необходимо откладывать по 1 миллиону, чтобы получить эти самые десять миллионов. Считается это элементарно:
10:1=10
Мы не будем откладывать деньги «под подушку», а отнесем их в банк. И, следовательно, ежегодно на те вклады, которые мы принесем в банк, будут начисляться проценты. Допустим, мы выбираем надежный, но при этом более-менее прибыльный банк, и поэтому ваши вклады ежегодно будут расти на 15% годовых. Другими словами можно сказать, что сумма на наших счетах ежегодно будет увеличиваться в 1,15 раза.
S0 – начальная сумма вклада
Давайте посчитаем, сколько денег будет на наших счетах после каждого года:
В первый год, когда мы только начнем откладывать деньги, никакие проценты не накопятся, т. е в конце года мы отложим 1 миллион рублей:
S0
В конце второго года на 1 миллион рублей, которые остались с первого года, уже будут начислены проценты, т.е. нам нужно умножить на 1,15. Однако в течение второго года мы также доложили еще 1 миллиона рублей. Разумеется, на этот миллион еще не были начислены проценты, потому что к концу второго года этот миллион только появился на счету:
S0⋅1,15+S0
Итак, третий год. В конце третьего года на эту сумму будут начислены проценты, т. е. необходимо всю эту сумму умножить на 1,15. И опять же, в течение всего года вы усердно работали и еще отложили 1 миллион рублей:
(S0*1,15+S0)1,15+S0
Давайте рассчитаем еще четвертый год. Опять же, вся сумма, которая оказалась у нас к концу третьего года, умножается на 1,15, т.е. на всю сумму будут начислены проценты. В том числе, будут начислены проценты на проценты. И к этой сумме добавляется еще 1 миллион, потому что в течение четвертого года вы также работали и также откладывали деньги:
((S⋅1,15+S)⋅1,15+S)1,15+S
А теперь давайте раскроем скобки и посмотрим, какая у нас будет сумма к концу четвертого года откладывания денег:
((S0⋅1,15+S0)⋅1,15+S0)1,15+S0==(S0⋅1,152+S0⋅1,15+S0)1,15+S0==S0⋅1,153+S0*1,152+S0⋅1,15+S0==S0*(1,153+1,152+1,15+1)==S0*(1+1,15+1,152+1,153)
Как видим, в скобках у нас стоит сумма элементов геометрической прогрессии.
Напомню, что если геометрическая прогрессия задана элементом b1, а также знаменателем q, то сумма элементов будет считаться по следующей формуле:
Sn=b1⋅(qn−1)/(q−1)
Эту формулу обязательно нужно знать и четко применять.
Обратите внимание: формула n -го элемента звучит следующим образом:
bn=b1⋅qn-1
b1=1; q=1,15
Теперь мы можем посчитать сумму:
s4=1⋅(1,154−1)/(1,15−1)
Посчитаем числитель отдельно:1.154 = 1,75
Итак, возвращаясь к сумме геометрической прогрессии, мы получим:
S4=1⋅(1,75−1)/0,15=1*(0,75)/0,15= 5
В итоге мы получаем, что за четыре года накоплений наша исходная сумма увеличится не в четыре раза, как если бы мы не клали деньги в банк, а в 5 раз, т. е. 5 миллионов рублей.
Если бы мы копили не четыре года, а пять лет, то в итоге наша сумма накоплений увеличилась бы в 6,7 раза:
S5=1⋅(2,01−1)/0,15=1*(1)/0,15= 6,7
Другими словами, к концу пятого года мы бы получили на счету следующую сумму:
6,7⋅1=6,7 млн.руб.
К концу 6 года имеем
S6=1⋅(2,31−1)/0,15=1*(1,31)/0,15= 8,7 млн.руб.
К концу 7 года
S7=1⋅(2.65−1)/0,15=1*(1,65)/0,15= 11млн. руб.
Таким образом, общий счет накоплений за счет банковских процентов снизился бы почти с 10 лет до 7 лет, т. е. почти на 3года.
Таким образом, даже, несмотря на то, что банк начисляет достаточно низкий процент на наши вклады (15%), уже через пять лет эти самые 15% дают прибавку, существенно превышающую наш ежегодный заработок. При этом основной мультипликационный эффект приходится на последние годы и даже, скорее, на последний год накоплений.
А вот что действительно полезно во всех этих рассуждениях, так это формула, которая позволяет нам найти итоговую сумму вклада через размер ежегодных платежей, а также через проценты, которые начисляет банк. Так и запишем:
Процентная ставка a%, сумма вклада будет увеличиваться каждый год в к=1+а/1оо раз.
Вклад=платеж начальный*(кn – 1)/k-1
Формула для вычисления вклада S=S0 *(kn-1)/k-1
2. Схемы выплаты кредитов.
В мировой практике существует и работает 2 способа погашения кредитов: Дифференцированный, при котором периодический платеж включает постоянную сумму для погашения основного долга по кредиту, к которой прибавляются проценты на оставшуюся часть долга и Аннуитетный - равными платежами.
Давайте детально рассмотрим схему погашения кредитов: аннуитетную и классическую.
Это необходимо, чтобы ориентироваться в условиях задач на кредиты. Рассмотрим, чем эти схемы отличаются друг от друга, в чем преимущества, недостатки каждой из них.
I. Классическая (стандартная, дифференцированная) схема погашения кредита.
Принцип действия: Ежемесячный платеж по кредиту состоит из двух частей:
1) Тело кредита — постоянная часть платежа (общая сумма задолжности разбивается на количество месяцев пользования кредитом).
2) Проценты — переменная часть платежа (начисляются исходя из фактического остатка задолжности).
Таким образом, общая сумма платежа по кредиту при классической схеме погашения происходит за счет уменьшения суммы процентов. В первый месяц платеж по кредиту будет максимальным, а в последний месяц — минимальным (будет состоять практически только из тела кредита).
Преимущества:
- Суммарная переплата за весь период пользования кредитом будет меньше, чем при использовании аннуитетной схемы погашения кредита;
- Всегда можно четко определить свой остаток задолжности;
- Выгодно погашать кредит досрочно: при досрочном погашении снижается сумма последующих платежей (за счет уменьшения процентов),
появляется возможность не погашать в последующие месяцы тело кредита (если оно уплачено наперед).
Недостатки:
- В первые месяцы совокупный платеж по классической схеме больше, чем по аннуитетной.
Кому выгоден:
- Заемщикам, которые заботятся о своем личном бюджете и желают выбрать кредит с наименьшей суммарной переплатой;
- Заемщикам, планирующим досрочное погашение кредита.
В последние годы классическую схему погашения кредита можно встретить все реже. Банки стараются переходить на использование аннуитетной схемы, которая является более выгодной для них, но менее выгодной для заемщиков.
2.Аннуитетная схема погашения кредита.
Принцип действия:
Ежемесячный платеж по кредиту состоит из одной фиксированной суммы, которая не меняется на протяжении всего срока пользования данными средствами. Размер этого платежа рассчитывается по формуле. Аннуитетный платеж включает в себя и погашение тела кредита, и погашение процентов; с каждым месяцем меняется только соотношение этих двух составляющих, но общая сумма платежа остается неизменной.
Аннуитетная схема погашения кредита устроена так, что в первые месяцы заемщик погашает больше процентов и меньше тело кредита, благодаря этому растет суммарная переплата по кредиту (т.к. проценты начисляются на большие суммы в сравнении с классической схемой.) Особенно это ощутимо на долгосрочных кредитах, например – ипотечных.
Преимущества:
-В первые месяцы пользования кредитом аннуитетный платеж будет меньше, чем суммарный платеж по классической схеме.
-Фиксированная сумма аннуитетного платежа позволяет максимально точно планировать личный бюджет.
Недостатки:
-Суммарная переплата будет больше за весь период пользования кредитом, чем при использовании классической схемы погашения кредита. При этом, чем больше срок кредитования, тем существеннее будет разница в переплате.
-Досрочные погашения: менее выгодно, чем при классической схеме (Выплачивая последние аннуитетные платежи наперед).
Кому выгодно:
-Банкам
-Заемщикам, у которых не хватает средств для погашения первых крупных платежей по классической схеме.
Рассмотрим Аннуитетный платеж с практической точки зрения:
1. Представим алгоритм решения задач на аннуитетный способ погашения кредита:
Введем обозначения
S0-сумма кредита
a%-процентная ставка
n- срок кредитования
Сумма выплат
31 декабря каждого года оставшаяся сумма долга попадает под банковские проценты (т.е. увеличивает долг на a%), затем заемщик переводит очередной транш.
1. 31 декабря каждого года сумма долга умножается на коэффициент
ϐ=1+ 
2. Пусть платеж – х
3. Сумма долга составит:
4. 1 год: S1=S0 *ϐ-х.
2 год: S2 = S1* ϐ -x = (S0* ϐ -x)* ϐ -x = S0* ϐ 2- ϐ x-x= S0* ϐ 2-x( ϐ +1).
3 год: S3=S2*ϐ-x=(S* ϐ 2-x( ϐ +1))* ϐ -x = S* ϐ 3-x ϐ ( ϐ +1)-x= =S* ϐ 3- x( ϐ ( ϐ +1)+1)=S* ϐ 3- x ( ϐ2+ϐ+ 1).
ϐ2+ϐ+ 1- Геометрическая прогрессия
ϐ1=1; q= ϐ
Формула суммы членов геометрической прогрессии
Sn= 
Тогда: Sn= 
S3= S* ϐ 3- x* 
4 год: S4= S* ϐ 4- x= S* ϐ 4- x( 1 + ϐ + ϐ2 + ϐ3 )= S* ϐ 4- x* 
Допустим, кредит должен быть выплачен за 4 года, тогда:
S4=0
S* ϐ 4- x*  =0
=0
Если зададим:
S= 6902000
a%=12,5
Найти X-ежемесячный платеж
X =  =
=  =
=  =
=  =
=  =
=  =
=  =0,35*812*103=350*812= 2296350
=0,35*812*103=350*812= 2296350
Подведем итоги:
ϐ=1+ 
Sn=  -Формула суммы n-членов геометрической прогрессии
-Формула суммы n-членов геометрической прогрессии
Сумма долга:
Sn=S0* ϐ n- x* 
2)Рассмотрим теперь алгоритм решения задач по кредитам, если выплаты строятся по дифференцированной схеме.
Исходные данные: n- срок заема, S0- сумма кредита, % ставка- a.
По данной схеме заемщик производит платежи так, чтобы долг уменьшался после каждого платежа на одну и ту же сумму.
1) Рассчитаем сумму выплат по процентам:
- Пусть S0 – сумма кредита, основной долг уменьшается равномерно 
- Первого числа долг возрастает на a%,
Тогда сумма выплат по процентам
1 период: (S0 -  ) *
) *  ;
;
2 период: (S0 -  -
-  ) *
) *  = (S0 -
= (S0 -  ) *
) *  ;
;
3 период: (S0 - 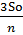 ) *
) * 
Тогда сумма выплат
S0 *  + (S0 -
+ (S0 -  ) *
) *  + (S0 -
+ (S0 -  ) *
) *  + (S0 -
+ (S0 - 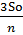 ) *
) * 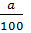 + (S0 -
+ (S0 -  ) *
) * 
=  * (1 + (1 -
* (1 + (1 -  ) + (1 -
) + (1 -  ) + (1 -
) + (1 -  ) + (1 –
) + (1 – 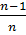 )) =
)) =  * (n + (n-1) + (n-2) + 1)
* (n + (n-1) + (n-2) + 1)
= 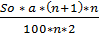 =
= 
Формула суммы n-членов арифметической прогрессии: Sn =  * n
* n
В нашем случае a1 = n; an = 1, тогда Sn =  * n
* n