Министерство Образования Российской Федерации
Вятский Государственный Гуманитарный Университет
Математический факультет
Кафедра математического анализа и МПМ
Выпускная квалификационная работа
Операторы проектирования.
Выполнил студент 5курса
математического факультета
Лежнин В.В.
/подпись/
 |
Научный руководитель:
Старший преподаватель кафедры математического анализа и МПМ
Гукасов А.К.
/подпись/
 |
Рецензент:
Старший преподаватель кафедры математического анализа и МПМ
Подгорная М.И.
/подпись/
|
Допущена к защите в ГАК
Зав. кафедрой М.В. Крутихина
/подпись/ << >>
Декан факультета В.И. Варанкина
/подпись/ << >>
Киров
Оглавление.
Введение. 2
Часть I. Основные понятия и предложения. 2
Часть II. Дополняемость в гильбертовых пространствах. 10
Часть III. Задача о дополняемости. 13
Литература. 15
Введение.
В данной работе рассматриваются операторы проектирования, которые являются частным случаев линейных операторов, их некоторые свойства, и рассматривается вопрос: как с помощью операторов проектирования можно выяснить дополняемо множество или нет. Так же освящается тема дополняемости в гильбертовых пространствах. Попутно для рассмотрения предлагаются некоторые определения и факты, на которые опираются нужные нам утверждения. К самостоятельно выполненным заданиям относятся доказательство замкнутости ядра (стр. 6, предложение 2), формула изменения коэффициентов Фурье при сдвиге на некоторое вещественное число и решение задачи о дополняемости.
|
|
Часть I. Основные понятия и предложения.
Определение. Метрику d на векторном пространстве X будем называть инвариантной, если d(x+z,y+z)=d(x,y), для любых x,y,z из X.
Определение. Пусть d – метрика на множестве X. Если каждая последовательность Коши сходится в X к некоторой точке, то d называется полной метрикой на X.
Определение. Векторное пространство X называется нормированным пространством, если каждому элементу x из X сопоставлено неотрицательное вещественное число 
, именуемое нормой x, и выполняются следующие условия:
1. 
£ + 
"x, yÎX.
2. 
= 
"xÎX, "a - скаляра.
3. > 0, если x¹0.
Примеры нормированных пространств.
1) l 
- нормированное пространство, в котором элементы – последовательности комплексных чисел x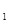=(x 
, …,x 
, …), удовлетворяющие условию 
<¥,
норма в таком пространстве определяется 
;
2) L (0,1) - нормированное пространство, состоящее из функций с интегрируемым квадратом на интервале (0, 1), удовлетворяющее условию 
dx < ¥, и норма определена как 
= 
.
3) С 
[0, 2p] – пространство непрерывных 2p периодических функций на отрезке [0, 2p]. Норма в нем определяется = 
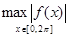
Определение. Пусть X, Y – два топологических линейных пространства. Линейным оператором, действующим из X в Y, называется отображение y = Ax, где x принадлежит X, а y принадлежит Y, удовлетворяющее условию
A(ax 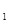+bx 
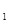) = aAx +bAx .
Определение. Оператор A называется непрерывным в точке x 
области определения, если для любой окрестности V точки y = Ax существует такая окрестность U точки x 
, что Ax принадлежит V, как только x принадлежит пересечению области определения и U. Оператор A называется непрерывным, если он непрерывен в каждой точке области определения.
|
|
Определение. Линейныйоператор, действующий изЕ в Е 
, называется ограниченным, если он определен на всем Е и каждое ограниченное множество переводит снова в ограниченное.
Предложение 1. Всякий непрерывный линейный оператор ограничен.
Доказательство.
Пусть М – подмножество ограниченного множества Е, а подмножество АМ множества Е 
не ограничено. Тогда в Е найдется такая окрестность нуля V, что ни одно из множеств 
АМ не содержится в V. То тогда существует такая последовательность х 
из М, что ни один из элементов Ах 
не принадлежит V, и получается, что х ® 0 в Е, но последовательность { Ах } 
не сходится к 0 в Е 
, а это противоречит непрерывности оператора А.
В нормированных пространствах определение ограниченности линейных операторов можно сформулировать так: оператор А ограничен, если существует такая постоянная С, что для всякого f из Е
.
Наименьшее из чисел С, удовлетворяющее этому неравенству, называется нормой оператора А и обозначается 
.
Определение. Пусть X - векторное пространство. Линейное отображение P:X → X называется проектором в пространстве X, если 
, т.е. P(P(x)) = Px для любого элемента x из X.
Свойства проекторов.
Пусть P проектор в X с ядром N(P) и образом R(P).
1. R(P) = N(I-P) = {xÎX, Px = x}, где I – тождественное отображение;
2. R(P)ÇN(P) = {0} и X = R(P)+N(P);
Доказательство 1.
а) Так как (I-P)P = IP- 
= P-P = 0, то R(P) содержится в N(I-P);
б) Если x принадлежит N(I-P), то x-Px = 0, следовательно, x = Px принадлежит R(P), значит N(I-P) содержится в R(P);
Таким образом, из а) и б) следует, что R(P) = N(I-P).
|
|
Доказательство 2.
Если x принадлежит пересечению R(P) и N(P), то x=Px=0, а следовательно, R(P) и N(P) пересекаются по {0};
Для любого x из X можно представить в виде x=Px+(x-Px), где Px принадлежит R(P) и x-Px принадлежит N(P), значит X=R(P)+N(P);
Определение. М – замкнутое подпространство топологического векторного пространства X. Если в X существует такое замкнутое подпространство N, что X=M+N и MÇN={0}, то говорят, что М дополняемо в X и что X является прямой суммой подпространств X=MÅN.
Определение. Топологическое векторное пространство X называется F-пространством, если топология порождается некоторой полной инвариантной метрикой.