Задание 1. Тема: Пределы функций.
Основные теоремы о пределах.
Т1.  .
.
Т2.  .
.  ,
,  .
.
 ,
,  .
.
Т3. 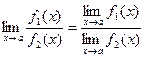 при
при 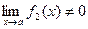 .
.
Основные пределы
1. 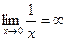 ,
, 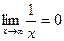 .
.
2. Первый замечательный предел: 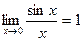 .
.
3. Второй замечательный предел: 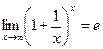 ,
, 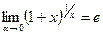 .
.
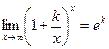 ,
,  ,
,  ,
,
 ,
, 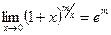 ,
, 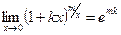 .
.
Пример.1 Найти пределы:
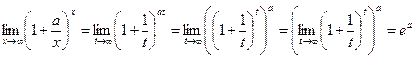
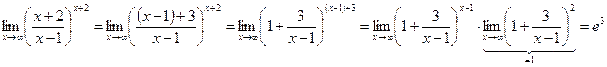
Основные эквивалентности:
Две бесконечно малые величины  и
и  называются эквивалентными при
называются эквивалентными при  , если
, если 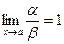 . Обозначение
. Обозначение  ~
~  .
.
Так, например, 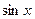 ~
~ 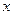 , т.к.
, т.к. 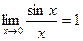 ,
, 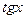 ~
~ 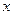 , т.к.
, т.к.  .
.
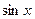 ~ ~ 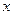 при при 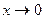
|  ~ ~ 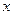 при при 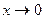
| ||
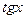 ~ ~ 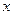 при при 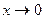
| 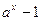 ~ ~  при при 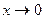
| ||
 ~ ~ 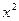 при при 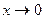
| 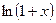 ~ ~ 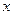 при при 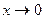
| ||
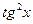 ~ ~ 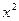 при при 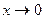
| 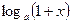 ~ ~ 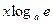 при при 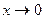
| ||
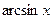 ~ ~ 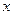 при при 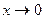
|  ~ ~ 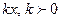 при при 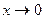
| ||
 ~ ~ 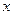 при при 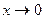
| 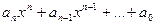 ~ ~ 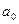 при при 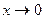
| ||
 ~ ~ 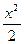 при при 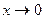
| 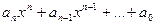 ~ ~  , , 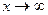
|
Вычисление пределов.
Если функция является элементарной и если предельное значение аргумента принадлежит ее области определения, то вычисление предела функции сводится к простой подстановке в функцию  предельного значения аргумента, т.е.
предельного значения аргумента, т.е. 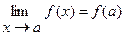 . Более сложными являются случаи нахождения пределов функций, где присутствуют неопределенности.
. Более сложными являются случаи нахождения пределов функций, где присутствуют неопределенности.
1. «неопределенность вида 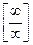 ». Делим числитель и знаменатель на
». Делим числитель и знаменатель на 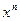 - максимальную степень.
- максимальную степень.
Пример 1.  .
.
Пример 2. 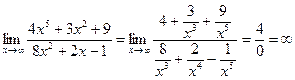 .
.
Пример 3. 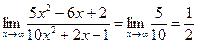 .
.
Таким образом, если функция под знаком предела представляет собой отношение многочленов 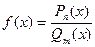 , то:
, то:
1) 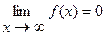 , если
, если 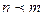 ;
;
2)  , если
, если 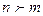 ;
;
3)  , если
, если 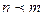 . Здесь
. Здесь  и
и 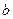 - коэффициенты при старших членах многочленов
- коэффициенты при старших членах многочленов 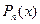 и
и 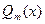 соответственно.
соответственно.
Так же вычисляются пределы от иррациональных функций.
2. «неопределенность вида 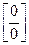 ». Для вычисления предела
». Для вычисления предела 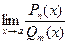 необходимо выделить в числителе и знаменателе дроби бином
необходимо выделить в числителе и знаменателе дроби бином 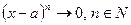 при
при  , с целью сокращения дроби на множитель, стремящийся к нулю.
, с целью сокращения дроби на множитель, стремящийся к нулю.
Пример 4. 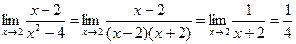 .
.
Пример 5.  . Разложим числитель и знаменатель дроби на множители
. Разложим числитель и знаменатель дроби на множители

Пример 6.  .
.
Сократим дробь, разделив числитель и знаменатель на 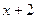 .
.
 и
и 

Вообще, если находится предел дроби, числитель и знаменатель которой многочлены, обращающиеся в нуль в предельной точке  , то согласно теореме Безу оба многочлена разделятся без остатка на
, то согласно теореме Безу оба многочлена разделятся без остатка на  , т.е. такую дробь всегда можно сократить на
, т.е. такую дробь всегда можно сократить на  .
.
Пример 7. Найти:  . Разложим числитель и знаменатель на множители, и сократим дробь на
. Разложим числитель и знаменатель на множители, и сократим дробь на 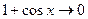 :
:

Пример 8.  . Умножим числитель и знаменатель на произведение
. Умножим числитель и знаменатель на произведение 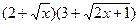 выражений, сопряженных числителю и знаменателю, и затем сократим дробь на
выражений, сопряженных числителю и знаменателю, и затем сократим дробь на 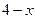 :
:
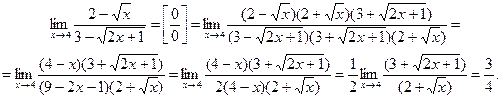
Пример 9. 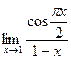 . Сделаем замену переменной:
. Сделаем замену переменной: 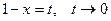 при
при 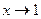 . Имеем
. Имеем

3. «неопределенность вида 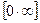 ». Необходимо перейти к неопределенности вида
». Необходимо перейти к неопределенности вида 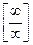 или
или 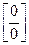 .
.
Пример 10.

4. «неопределенность вида  ». Переход к
». Переход к 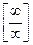 или
или  .
.
Пример 11.

5. «неопределенность вида  ». Необходимо использовать формулу второго замечательного предела или, для более сложных случаев, формулу
». Необходимо использовать формулу второго замечательного предела или, для более сложных случаев, формулу
 (*)
(*)
Пример 12. 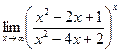 . Используем формулу (*).
. Используем формулу (*).
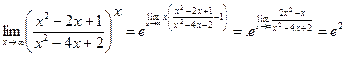 .
.
Пример 13.  . Используем формулу (*).
. Используем формулу (*).
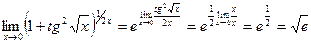 .
.
Задание 2. Тема: Непрерывность функции в точке.
Пусть функция  определена в точке
определена в точке 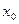 и в некоторой окрестности этой точки.
и в некоторой окрестности этой точки.
Функция  называется непрерывной в точке
называется непрерывной в точке 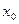 , если:
, если:
1) она определена в этой точке;
2) $ 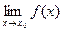 ; и 3) этот предел равен значению функции в точке
; и 3) этот предел равен значению функции в точке 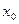 , т.е.
, т.е.
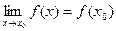 . (1)
. (1)
Если хотя бы одно из этих условий не выполняется, то функция называетсяразрывной в точке 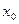 . Точки, в которых нарушается непрерывность функции, называются точками разрыва.
. Точки, в которых нарушается непрерывность функции, называются точками разрыва.
Различают два вида точек разрыва для функции  :
:
І.Точка разрыва первого рода – точка 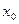 , в которой существуют конечные пределы функции слева и справа (односторонние пределы), т.е.
, в которой существуют конечные пределы функции слева и справа (односторонние пределы), т.е.  и
и 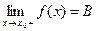 , причем, если:
, причем, если:
а) 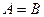 , то
, то 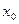 называется точкой устранимого разрыва;
называется точкой устранимого разрыва;
б) 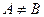 , то
, то 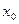 называется точкой конечного разрыва, при этом величину
называется точкой конечного разрыва, при этом величину  называют скачком функции.
называют скачком функции.
ІІ. Точка разрыва второго рода – точка 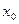 , в которой, по крайней мере, один из односторонних пределов не существует или равен бесконечности (бесконечный разрыв).
, в которой, по крайней мере, один из односторонних пределов не существует или равен бесконечности (бесконечный разрыв).
Пример 1. Функция  в точке
в точке 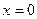 имеет бесконечный разрыв (второго рода), т.к.
имеет бесконечный разрыв (второго рода), т.к.  , при этом в точке
, при этом в точке 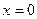 функция не определена.
функция не определена.
Вспомним понятия односторонних пределов:
О. Если  стремится к пределу
стремится к пределу  при
при  так, что
так, что 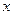 принимает только значения, меньшие
принимает только значения, меньшие  , то
, то  называют пределом функции
называют пределом функции  слева в точке
слева в точке  ,если же
,если же  стремится к пределу
стремится к пределу 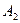 при
при  так, что
так, что 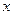 принимает только значения, большие
принимает только значения, большие  , то
, то 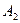 называют пределом функции
называют пределом функции  справа в точке
справа в точке  .
.
У нас функция  при
при 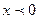 , т.к.
, т.к.  . И функция
. И функция  при
при 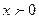 , т.к.
, т.к.  .
.
Пример 2. Функция  в точке
в точке 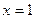 имеет конечный разрыв (первого рода), так как
имеет конечный разрыв (первого рода), так как 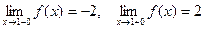 , при этом функция
, при этом функция  определена всюду, кроме точки
определена всюду, кроме точки 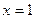 . Скачек функции в этой точке равен 2-(-2)=4. Рисунок:
. Скачек функции в этой точке равен 2-(-2)=4. Рисунок:
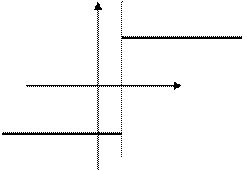
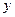
0 1 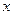
-2
Задание 3. Тема: Производная функции.
Основные правила дифференцирования
Пусть функции  и
и 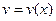 - две дифференцируемые в некотором интервале
- две дифференцируемые в некотором интервале 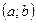 функции.
функции.
1.  .
.
2.  ,
, 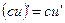 ,
, 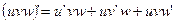 .
.
3.  .
.
4. Если функция  имеет производную
имеет производную  в точке
в точке 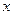 , а функция
, а функция  имеет производную
имеет производную  в соответствующей точке
в соответствующей точке  , то сложная функция
, то сложная функция  имеет производную
имеет производную  в точке
в точке 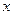 , которая находится по формуле
, которая находится по формуле  .
.
Производные основных элементарных функций.
1.  ,
, 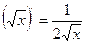 ,
, 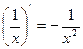
2. 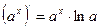 ,
, 
3.  ,
, 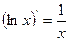
4. 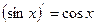 ,
, 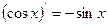 ,
,  ,
, 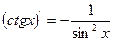
5.  ,
,  ,
, 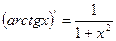 ,
, 
6. 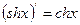 ,
,  ,
, 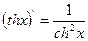 ,
, 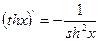
Дифференцирование неявных функций
Функция, заданная уравнением 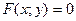 , не разрешенным относительно
, не разрешенным относительно 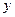 , является неявно заданной функцией аргумента
, является неявно заданной функцией аргумента 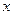 . Для нахождения производной функции
. Для нахождения производной функции 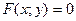 достаточно:
достаточно:
1) продифференцировать обе части равенства по переменной 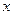 , (
, (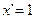 , а производная от
, а производная от 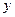 равна
равна  );
);
2) полученное уравнение разрешить относительно  .
.
Пример 1. Найти  , если
, если  .
.
 ,
,

Пример 2. Найти  , если
, если 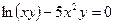 .
.
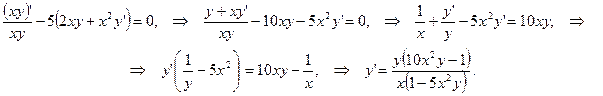
Дифференцирование параметрически заданных функций
Функция  , заданная параметрически имеет вид
, заданная параметрически имеет вид
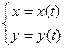 ,
,
где 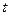 - вспомогательная переменная (параметр), а функции
- вспомогательная переменная (параметр), а функции 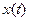 и
и  дифференцируемы по
дифференцируемы по 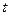 . Производные первого и второго порядка находятся по формулам:
. Производные первого и второго порядка находятся по формулам:
 и
и 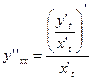 соответственно.
соответственно.
Пример 3. Найти  функции
функции 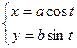 .
.
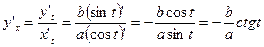 - производная первого порядка.
- производная первого порядка.
Тогда  - производная второго порядка.
- производная второго порядка.
Логарифмическое дифференцирование (ЛД)
Дифференцирование многих функций значительно упрощается, если их предварительно прологарифмировать.
ЛД полезно применять, когда заданная функция содержит логарифмирующиеся операции (умножение, деление, возведение в степень, извлечение корня). Кроме того, существуют функции, производные которых находят только лишь через операцию логарифмирования, например, показательно-степенная функция 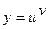 , где
, где  и
и 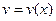 - дифференцируемые функции от
- дифференцируемые функции от 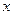 .
.
Найдем производную этой функции. Дифференцируем обе части равенства по основанию  :
:
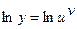 , или
, или  .
.
Теперь дифференцируем обе части равенства
 , Þ
, Þ  или
или 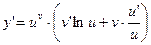 .
.
Пример 3. Найти производные следующих функций:
а)  ; б)
; б)  ; в)
; в) 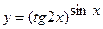 .
.
а)  , Þ
, Þ 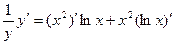 , Þ
, Þ 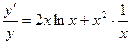 ,
,
Þ  , Þ
, Þ  - окончательный ответ.
- окончательный ответ.
б)  , Þ
, Þ  , Þ
, Þ
 , Þ
, Þ 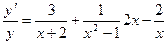 , Þ
, Þ
 - окончательный ответ.
- окончательный ответ.
в) 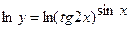 , Þ
, Þ 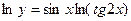 , Þ
, Þ  , Þ
, Þ 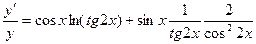 , Þ
, Þ
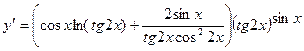 - окончательный ответ.
- окончательный ответ.
Примеры вычисления производных.
1. 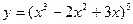 ,
, 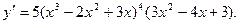 ;
;
2.  ,
, 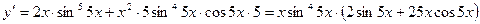 ;
;
3.  ,
, 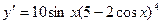 ;
;
4. 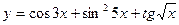 ,
, 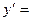
 ;
;
5. 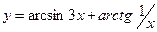 ,
, 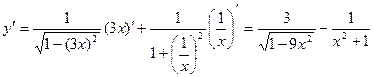 ;
;
6.  ,
, 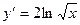
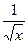
 ;
;
7. 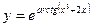 ,
, 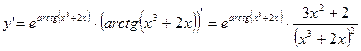 ;
;
Задание 5. Тема: Правило Лопиталя.
Т1. ( Правило Лопиталя раскрытия неопределенности вида 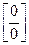 ). Пусть функции
). Пусть функции  и
и 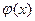 дифференцируемы в некоторой окрестности точки
дифференцируемы в некоторой окрестности точки  и обращаются в нуль в этой точке, т.е.
и обращаются в нуль в этой точке, т.е. 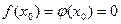 . Пусть
. Пусть  в окрестности точки
в окрестности точки  . Тогда, если существует предел
. Тогда, если существует предел  , то
, то
 .
.
Т2. ( Правило Лопиталя раскрытия неопределенности вида 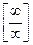 ). Пусть функции
). Пусть функции  и
и 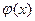 дифференцируемы в некоторой окрестности точки
дифференцируемы в некоторой окрестности точки  (кроме, быть может, самой точки
(кроме, быть может, самой точки  ) и в этой окрестности
) и в этой окрестности  . Тогда, если существует предел
. Тогда, если существует предел 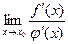 (
( ), то
), то
 .
.
Пример 1. Вычислить  .
.
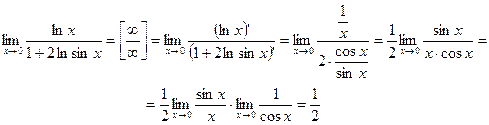
Пример 2. Вычислить 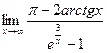 .
.

Пример 3.  .
.
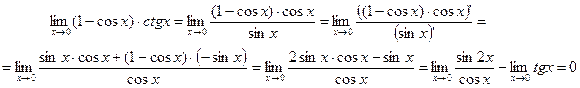
Пример 4.  .
.
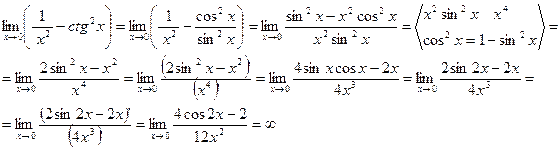
Пример 4.  .
.  Выведем формулу, удобную для применения в таком случае. Пусть
Выведем формулу, удобную для применения в таком случае. Пусть  . Логарифмируем:
. Логарифмируем: 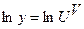 , Þ
, Þ 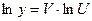 , откуда
, откуда  . Тогда
. Тогда
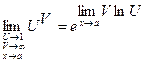 . (*)
. (*)

Пример 4.  .
.  . Используем формулу (*).
. Используем формулу (*).
 .
.
Формула (*) применяется и для случаев неопределенности вида  ,
,  .
.
Задание 6. Тема: Исследование функций и построение графиков.
Общее исследование функций и построение их графиков удобно выполнять по следующей схеме:
I. Область определения функции.
II. Элементы симметрии графика функции:
а) четность, нечетность; б) периодичность.
III. Непрерывность:
а) интервалы непрерывности;
б) поведение функции на границах интервалов непрерывности;
в) точки разрыва функции.
IV. Нули функции и интервалы знакопостоянства функции.
V. Асимптоты графика функции:
а) вертикальные; б) горизонтальные; в) наклонные.
VI. Экстремумы:
а) нахождение точек возможного экстремума (ТВЭ);
б) интервалы возрастания и убывания функции;
в) максимум, минимум функции.
VII. Выпуклость, вогнутость:
а) нахождение точек возможного перегиба (ТВП);
б) интервалы выпуклости и вогнутости функции;
в) точки перегиба.
VIII. Табуляция (дополнительные точки, минимум 20 точек).
IX. График функции.
X. Множество значений функции (по графику).
Пример. Исследовать и построить график функции  .
.
I. Функция  определена на всей числовой оси, кроме точки
определена на всей числовой оси, кроме точки 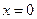 .
.
II. В точке 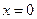 функция имеет бесконечный разрыв:
функция имеет бесконечный разрыв: 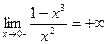 и
и  . Во всех других точках числовой оси функция непрерывна.
. Во всех других точках числовой оси функция непрерывна.
III. 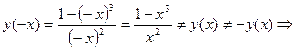 функция общего положения, т.е. график не имеет симметрии. Функция непериодическая.
функция общего положения, т.е. график не имеет симметрии. Функция непериодическая.
IV. Находим точки пересечения с осями координат:
а) с осью  :
: 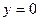 ,
, 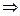
 ;
;
б) с осью 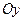 :
: 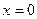 ,
, 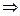 нет точек пересечения с осью
нет точек пересечения с осью 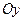 ,
,
Таким образом, график функции пересекает ось  в точке
в точке 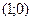 и не пересекает оси
и не пересекает оси 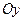 .
.
Слева от точки разрыва, при  ,
,  ; между точкой разрыва и точкой пересечения с осью
; между точкой разрыва и точкой пересечения с осью  , при
, при  ,
,  ; справа от точки пересечения с осью
; справа от точки пересечения с осью  , при
, при 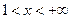 ,
,  .
.
V. Асимптоты.
а) 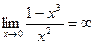 ,
, 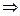 прямая
прямая 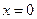 является вертикальной асимптотой;
является вертикальной асимптотой;
б)  ,
, 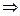 горизонтальных асимптот нет;
горизонтальных асимптот нет;
в)  ,
, 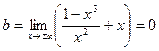 ,
, 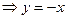 - наклонная асимптота.
- наклонная асимптота.
VI.  .
. 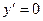 , Þ
, Þ 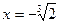 - ТВЭ;
- ТВЭ; 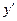 - не существует в точке
- не существует в точке 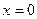 , но эта точка не является ТВЭ, т.к. она является точкой разрыва.
, но эта точка не является ТВЭ, т.к. она является точкой разрыва.
|
Слева от точки минимума при 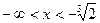 ,
, 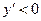 - функция убывает, между точкой минимума и точкой разрыва при
- функция убывает, между точкой минимума и точкой разрыва при 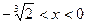 ,
, 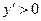 - функция возрастает; справа от точки разрыва при
- функция возрастает; справа от точки разрыва при  ,
, 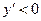 - функция убывает.
- функция убывает.
 .
.
VII. 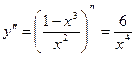 ;
;  ;
;  не существует при
не существует при 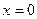 , но этаточка не может быть точкой перегиба, т.к. она является точкой разрыва. Следовательно, график функции не имеет точек перегиба. Во всей области определения функции
, но этаточка не может быть точкой перегиба, т.к. она является точкой разрыва. Следовательно, график функции не имеет точек перегиба. Во всей области определения функции  , поэтому ее график всюду обращен выпуклостью вниз (вогнут).
, поэтому ее график всюду обращен выпуклостью вниз (вогнут).
VIII. Табуляция (в Excel)
IX. График.
X. Множество значений 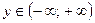
|

|
Задание 7. Тема: Комплексные числа.
Алгебраической формой комплексного числа (КЧ) называют число вида
 ,
,
где 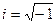 – мнимая единица – число, дающее в квадрате «-1». Частные случаи комплексного числа:
– мнимая единица – число, дающее в квадрате «-1». Частные случаи комплексного числа:
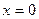 , Þ
, Þ  – мнимое число;
– мнимое число;
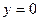 , Þ
, Þ 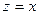 – действительное число.
– действительное число.
Число 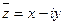 называется сопряженным числу
называется сопряженным числу  .
.
Тригонометрическая форма КЧ:
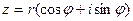 , (1)
, (1)
где 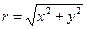 -модуль КЧ., угол
-модуль КЧ., угол  - главное значение аргумента КЧ. Связь между
- главное значение аргумента КЧ. Связь между 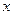 ,
, 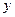 и
и  такая же, как между декартовыми и полярными координатами точки:
такая же, как между декартовыми и полярными координатами точки:
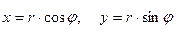 ;
;
В частности:
- для действительного положительного числа 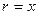 ,
, 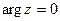 ;
;
- для действительного отрицательного числа 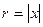 ,
, 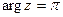 ;
;
- для мнимого положительного числа  ,
,  ;
;
- для мнимого отрицательного числа 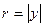 ,
,  .
.
Пример 1. Записать КЧ 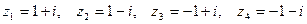 в тригонометрической форме.
в тригонометрической форме.
Модуль для всех чисел 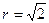 . Аргументы:
. Аргументы:
- для 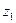 :
:  , так как
, так как 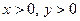 ,
,  - в І четверти;
- в І четверти;
- для  :
:  , так как
, так как 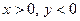 ,
,  - в ІU четверти;
- в ІU четверти;
- для 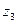 :
: 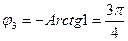 , так как
, так как 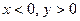 ,
, 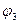 - во ІІ четверти;
- во ІІ четверти;
- для  :
: 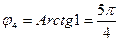 , так как
, так как  ,
, 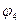 - в ІІІ четверти;
- в ІІІ четверти;
Показательная форма комплексного числа:  .
.
Здесь  - главное значение аргумента КЧ.
- главное значение аргумента КЧ.
Например, число  , данное в алгебраической форме, может быть записано в тригонометрической форме
, данное в алгебраической форме, может быть записано в тригонометрической форме  и в показательной форме
и в показательной форме  .
.
Действия над комплексными числами
Пусть даны 2 комплексных числа 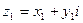 и
и  .
.
1. Сложение, вычитание:
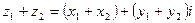 ,
, 
2. Умножение:
 .
.
В частности 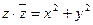 - действительное число. Надо помнить, что
- действительное число. Надо помнить, что 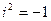 .
.
Например:  ,
, 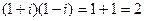 .
.
3. Деление:
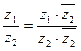 .
.
Например: 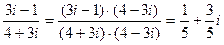 .
.
4. Возведение в степень.
Возведение комплексного числа в  - ю степень производится по формуле Муавра:
- ю степень производится по формуле Муавра:
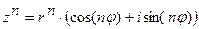 .
.
Формула Муавра применима при любом  : дробном, положительном, отрицательном. При дробном
: дробном, положительном, отрицательном. При дробном  необходимо учитывать многозначность результата.
необходимо учитывать многозначность результата.
В частности, имеем:  ,
, 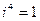 ,
, 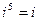 ….
….
Например: Пусть  , тогда
, тогда
 .
.
5.Извлечение корня  -й степени.
-й степени.
Как действие, обратное возведению в степень, производится по формуле Муавра для дробного показателя
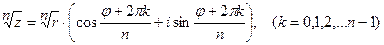 .
.

 Геометрически, значения корня
Геометрически, значения корня  являются вершинами правильного
являются вершинами правильного  - угольника, вписанного в окружность с центром в начале координат радиуса R=
- угольника, вписанного в окружность с центром в начале координат радиуса R=  .
.

 Пример 1. Вычислить все значения
Пример 1. Вычислить все значения 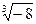 .
.
Имеем  , откуда
, откуда


 .
.
При 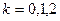 получим
получим 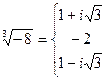 .
.
Построение точек