Пусть дан вектор на координатной плоскости. Как его можно записать? (Координатами (х,у).) А в пространстве? (x,y,z)А в каком пространстве живем мы? (4, (x,y,z,t)). Пара чисел (x,y) называется двухмерным вектором, тройка чисел (x,y,z) - трехмерным, (x,y,z,t)- четырехмерным. Их вводят для краткости записей и рассматривают как один элимент. Вектора можно обозначать, опять же для краткости. 
В общем виде можно вектор можно записать так 
. Это n-мерный вектор. Вектора бывают и бесконечномерные, но их мы рассматривать не будем.
Задание 1. Приведите примеры векторов.
Каким образом записывают результаты футбольных матчей? (При помощи таблиц.)
Пусть в группе В играли пять команд по круговой системе. Результаты игры отображены в таблице.
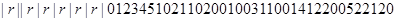
Где 2- победа,1- ничья,0- поражение.
Эту таблицу также можно назвать матрицей.
Опр. Таблицу вида
будем называть матрицей размерности 
.
Для краткости будем обозначать матрицы большими латинскими буквами.
Вектор является частным случаем матрицы при m=1.
1.3.3 Умножение матриц. Свойства
Как сложить две матрицы?
Опр. Суммой матриц 
и 
размерности 
называется матрица 
размерности .
Пример.
Как суммировать матрицы вы уже знаете. Теперь придумайте как умножить матрицу на число.
Опр. Произведением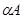 
матрицы 
размерности и числа 
называется матрица 
размерности .
Пример.
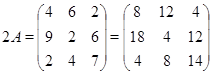
Кроме введенных операций нам понадобится умножение матриц.
Опр. Произведением матриц 
и 
называется матрица 
, где 
Необходимо показать и озвучить практический способ умножения матриц: строка умножается на столбец. Берем первую строку матрицы А, ставим ее вертикально напротив первого столбца матрицы В, умножаем элементы этой строки и столбца, которые стоят напротив др.др., складываем произведения. Это первый элемент матрицы С. Теперь таким же образом умножаем эту строку на второй столбец - получаем второй элемент первой строки матрицы С. И т.д. Получим первую строку новой матрицы. Для того, чтобы получить вторую строку, проделываем тоже самое со второй строкой матрицы А.
Пример.
Задача 1. Выполнить умножение.
1.3.4 Домашнее задание
Задача 2. Выполнить умножение.
Четвертый урок
1.4.1 Проверка домашнего задания
1.4.2 Транспонирование
Опр. Замена строк матрицы на ее столбцы (а стольбцов на строки) называется транспонированием. Обозначается 
.
Пример.
1.4.3 Определитель матрицы
Поставим каждой матрице по определенному правилу в соответствие число и назовем его определителем матрицы.
Например:
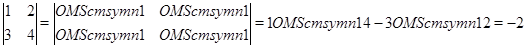
Таким образом вычисляют определители двхмерной и трехмерной матриц. Эта схема вычисления называется мнемоническим правилом. Для четырехмерной матрицы не удобно составлять такие схемы. Существует строгое правило нахождения определителя матрицы n-го порядка. Но мы будем работать только с трехмерными матрицами.
Необходимо обратить внимание на то, что матрица пишется в круглых скобках, а определитель матрицы - в прямых.
Задача 1. Найти определители матриц А и из Примера.
Обратить внимание, на то что определитель матрицы не совпадает с определителем транспонированной матрицы.
Задача 2. Найти определители матриц.
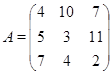
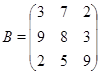
1.4.4 Домашнее задание
Задача 3. Найти произведение матриц А и В из задачи 2. Вычислить определитель полученной матрицы.
Задача 4. Найти значение выражения 
. Матрицы из задачи 2.
Необходимо сказать, что последовательность выполнения операций, такая же как и для чисел, но первым выполняют транспонирование.
Пятый урок
1.5.1 Проверка домашнего задания
1.5.2 Обратная матрица
Опр. Если 
, то 
обозначают 
и пишут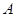 
.
Где 
- матрица с единицами на главной диагонали и нулями на остальных местах. Показать главную диагональ.
Для того, чтобы найти обратную матрицу нам необходимо найти т.н. алгебраическое дополнение.
Пусть дана матрица
число
называется алгебраическим дополнением элемента 
. Алгебраическое дополнение можно найти для любого элемента матрицы.
Опр. Алгебраическим дополнением элемента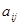 
называется произведение 
на определитель матрицы после вычеркивания из нее i-й строки и j-го столбца.
Теперь можно найти и обратную матрицу.
Задача 1. Найти обратную матрицу.
3.5.3 Домашнее задание
Задача 1. Найти обратную матрицу.
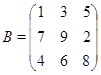
Шестой урок
1.6.1 Математическая постановка задачи
Итак, имеем две рисковые ц.б., заданные таблицей роста/падения цен и одну безрисковую, заданную процентом годовых. Необходимо сформировать портфель максимальной эффективности.
Доходность безрисковой ц.б. 
.
Если сегодня стоимость портфеля 
, а через год она окажется равной 
, то 
естественно назвать доходностью портфеля в процентах годовых. Т.е. доходность портфеля - это доходность на единицу стоимости.
Аналогично доходности всего портфеля находится доходность каждого вида акций. Т.е. нам нужно составить таблицу доходностей для ц.б. первого и второго видов. Например, для ц.б. первого вида доходность за первый год будет 
, за второй год - 
. Таким образом находим доходности за все 12 лет для каждого вида акций. Получаем таблицу с двумя столбцами и 11 строками.
Как правило, доходность бумаг колеблется во времени, так что будем считать ее случайной величиной. Найдем среднюю ожидаемую доходность 
и среднее квадратичное отклонение 
И назовем их соответственно эффективностью и риском i-ой ценной бумаги. Эффективностью портфеля назовем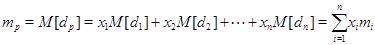 
. Т.е. математическое ожидание доходности портфеля.А величину 
(1) (где 
-ковариация i-ой и j-ой с.в.) назовем риском рисковой части портфеля портфеля.
Обозначим 
- доля безрисковой ц.б. в портфеле. 
- вектор долей первой и второй ц.б. 
. Тогда естественно, должно выполнятся равенство 
. Пусть 
-ожидаемая эффективность бумаг. V- матрица 
ковариаций ценных бумаг. 
-риск портфеля.
Используя введенные обозначения, поставим математическую задачу. Как отмечалось выше: . Если возвести обе части равенства (1) в квадрат и записать в матричной форме, то получим 
. И теперь основное: необходимо добиться максимального значения эффективности портфеля, т.е. 
.
1.6.2 Решение задачи
Решение задачи найдем по формуле:
.
В результате проделанных операций получим двухмерный вектор - доли рисковых акций в портфеле. Доля безрисковой акции в портфеле найдется из равенства .
Находить решение поставленной задачи удобнее разбив формулу по действиям. Если учащиеся хорошо усвоили предыдущий материал, то вычисления не вызовут ни каких затруднений, т.к. не содержат нового материла.
Седьмой урок
Напомнить результаты постановку математической задачи. Записать результ, к которому пришли на прошлом уроке. Продолжить решение.
Доли акций могут оказаться больше 1, или даже отрицательными. Если доля акции отрицательная - необходимо пройзвести операцию short sale. Суть этой операции состоит в следующем: инвестор, формирующий портфель, обязуется через какое-то время поставить бумаги i-го вида (вместе с доходом, который они принесли бы владельцу за это время). За это он сейчас получает их денежный эквивалент. Эти деньги он присоединяет к своему капиталу и покупает рекомендуемые оптимальным решением ц.б. Т.к. ценные бумаги других видов более эффективны, то инвестор оказывается в выигрыше. Можно обойтись и без операции short sale, если инвестору доступны займы денежных средств по безрисковой ставке. Тогда налагают дополнительное условие 
Заключение
В результате проделанной работы был составлен факультативный курс по теме "Оптимальный портфель ценных бумаг". Он позволяет учащимся профильных экономических классов глубже понять суть работы экономистов, увидеть тесную связь между математикой и экономикой, сделать профессиональный выбор. В ходе факультативных занятий школьники знакомятся с основными понятиями ТВиМС.
Факультатив содержит только необходимые для решения поставленной задачи (формирование оптимального портфеля Тобина максимальной эффективности из предложенных ценных бумаг) понятия. Однако, изученный материал позволяет сформировать у учащихся представление о ТВиМС.
Факультатив расчитан на 10, 11 профильные математические и экономические классы с высоким уровнем успеваимости. Проведенные в 10 экономическом классе МПГ №56 г.Гомеля занятия показали, что школьники способны усаваивать данный материал. Однако время уроков 2-6 необходимо увеличить до 2 академических часов.
Литература
1. Малыхин В.Н. "Оптимальный портфель и пакеты" м.: ОЛМА-ПРЕСС. 2000
2. Малыхин В.Н. "Финансовая математика" М.: ИНФРА-М, 1999
3. Маршалл Дж. "Финансовая инженерия" М.: ИНФРА-М, 1998
4. Малинковский Ю.В. Лекции по ТВиМС
5. Бузланов А.В. Лекции по алгебре и теории чисел
6. Журнал "Математика в школе", 1975-1985