Тема: «Массивы. Задачи комбинированной обработки массивов»

Вариант 21

 

1. Дан вектор A(n). Подсчитать количество полных квадратов. Если оно больше 2, то все элементы с четными номерами умножить на 2.

2. Дан целочисленный вектор A(n). Найти номер первого максимального значения среди отрицательных элементов, расположенных правее первого элемента, равного t.

3. Дана квадратная матрица A(nхn). Построить вектор b, где b_i, i =1,…, n – максимальный элемент i -ой строки матрицы, среди элементов, стоящих в четных столбцах.

4. Дана квадратная матрица A(nхn). Удалить строки, состоящие из одних нулей.

5. Дана квадратная матрица A(nхn). Найти сумму положительных элементов матрицы в заданной области.

 

6.* Даны матрицы A(mxn) и B(lxp) m>l, n>p состоящие из нулей и единиц. Проверить, можно ли наложить матрицу B на матрицу A (разрешается зеркально отображать матрицу B) так, чтобы каждой единице матрицы B соответствовал нуль в матрицу А, и если можно, то как (на сколько и в каком направлении следует подвинуть матрицу B по матрице A до выполнения условия)?

 

 

Лабораторная работа №3

Тема: «Массивы. Задачи комбинированной обработки массивов»

Вариант 22

 

1. Дан вектор A(n). Подсчитать количество элементов максимальных по величине и если оно больше 2, то все элементы вектора с четными индексами заменить на 0.

2. Найти номер первого максимального значения среди элементов, меньших a и расположенных правее первого элемента, кратного трем.

3. Дана квадратная матрица A(nхn). Построить вектор b, где b_i, i =1,…, n – максимальный элемент i -ого столбца матрицы, среди элементов, стоящих в четных строках.

4. Дана квадратная матрица A(nхn). Вставить после строки, содержащей наибольшее количество четных элементов строку, состоящую из максимальных элементов столбца.

5. Дана квадратная матрица A(nхn). Найти сумму отрицательных элементов матрицы в заданной области.

 

6.* Матрица А вводится построчно. Число строк заранее неизвестно, но различных строк не более m. Расположить ее в выделенном массиве, при этом повторяющиеся строки включать единожды.

 

 

Лабораторная работа №3

Тема: «Массивы. Задачи комбинированной обработки массивов»

Вариант 23

 

1. Дан вектор A(n). Если наименьший элемент вектора A находится на четном месте, то все элементы расположенные на нечетных местах умножить на 2. В противном случае вектор оставить без изменения.

2. Дан целочисленный вектор A(n). Найти максимальное значение среди отрицательных элементов, расположенных до первого элемента, равного t.

3. Дана квадратная матрица A(nхn). Построить вектор b, где b_i, i =1,…, n – среднее арифметическое положительных элементов i -ой строки матрицы.

4. Дана квадратная матрица A(nхn). Удалить столбцы, в которых есть хотя бы один отрицательный элемент.

5. 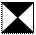Дана квадратная матрица A(nхn). Найти количество положительных элементов матрицы в заданной области.

 

6.* Для заданной целочисленной матрицы найти максимум среди сумм элементов диагоналей, параллельных главной диагонали матрицы.

 

 

Лабораторная работа №3

Тема: «Массивы. Задачи комбинированной обработки массивов»

Вариант 24

 

1. Дан вектор A(n). Все компоненты с нечетными индексами, предшествующие наибольшему элементу домножить на наименьший элемент вектора.

2. Дан целочисленный вектор A(n). Найти номер последнего максимального элемента среди элементов, лежащих в диапазоне [ a,b ]и расположенных до первого элемента с четным значением.

3. Дана квадратная матрица A(nхn). Построить вектор b, где b_i, i =1,…, n – среднее арифметическое положительных элементов i -ого столбца матрицы.

4. Дана квадратная матрица A(nхn). Удалить столбцы, содержащие четное число положительных элементов.

5. Дана квадратная матрица A(nхn). Найти количество отрицательных элементов матрицы в заданной области.

 

6.* Для заданной целочисленной матрицы найти минимум среди сумм модулей элементов диагоналей, параллельных побочной диагонали матрицы.

 

 

Лабораторная работа №3