Использование критерия NPV теоретически обоснованно, и в целом он считается наиболее корректным измерителем эффективности инвестиций. Вместе с тем применение абсолютных показателей при анализе проектов с различными исходными условиями (первоначальными инвестициями, сроками экономической жизни и др.) может приводить к затруднениям при принятии управленческих решений.
Пример 2.3
Предположим, что рассматриваются два проекта. Принятая норма дисконта составляет 10%. Соответствующие оценки денежных потоков и расчет NPV приведены в табл. 2.3.
Т а б 1 и ц а 2.3. Условия реализации проектов (пример 2.3)
| Проект | I0 | CFt | PV | NPV |
| X | -10000,00 | 16 500,00 | 15000,00 | 5 000,00 |
| Y | -100000,00 | 115 000,00 | 105 000,00 | 5 000,00 |
Чистая современная стоимость обоих проектов составляет 5000 и в случае необходимости выбора не позволяет однозначно определить лучший вариант. Поэтому наряду с абсолютным показателем эффективности инвестиций NPV используются также и относительные — индекс рентабельности и внутренняя норма доходности.
Индекс рентабельности (benefit-cost ratio, profitability index — РГ) показывает, сколько единиц современной величины денежного потока приходится на единицу предполагаемых первоначальных затрат. Для расчета этого показателя используется следующая формула
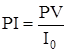
Если величина критерия PI > 1, то современная стоимость денежного потока проекта превышает первоначальные инвестиции, обеспечивая тем самым наличие положительной величины NPV. При этом норма рентабельности превышает заданную, и проект следует принять.
При PI = 1 величина NPV = О, и инвестиции не приносят дохода. Если PI<1, проект не обеспечивает заданного уровня рентабельности и его следует отклонить.
Общее правило PI: если Р1> 1, то проект принимается, иначе — его следует отклонить.
На Листе5 введите данные таблицы 2.3 и рассчитайте индексы рентабельности для примера 2.3 согласно формулам:.
Р1Х= 15000/ 10000= 1,50;
Ply = 105 000 /100 000 = 1,05.
Переименуйте Листе5 в PI.
Таким образом, проект X обеспечивает большую рентабельность инвестиций и в случае невозможности реализации обоих проектов ему следует отдать предпочтение.
Несмотря на то, что в ППП EXCEL нет специальной функции для вычисления индекса рентабельности, определить его можно довольно легко, например, делением ячейки, содержащей функцию расчета NPV, на ячейку, содержащую величину первоначальных инвестиций, и последующим прибавлением к результату единицы.
Рассчитаем индекс рентабельности для примера 2.1. Для этого в ячейке В20 листа NPV сформированной ранее таблицы задайте одну из следующих формул (рис. 2.6):
-B18 / В10 + 1 (Результат: 1,57)
-B19 / В610 + 1 (Результат: 1,57).
Знак минус в формуле необходим для получения положительного результата, так значение ячейки В6 (первоначальные инвестиции) — отрицательная величина. Сохраните полученную таблицу на магнитном диске.
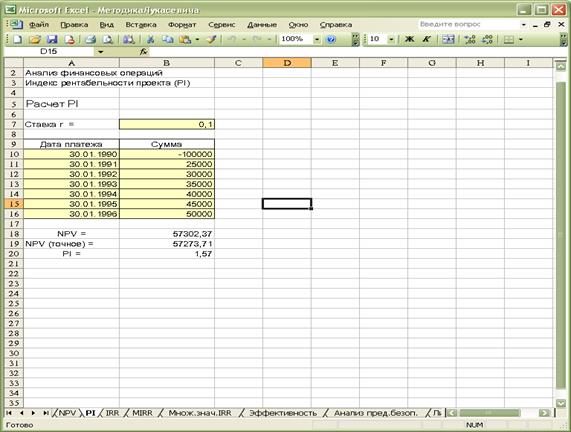
Рис. 2.6. Расчет индекса рентабельности
Применение показателя PI часто бывает полезным в случае, когда существует возможность финансирования нескольких проектов, но при этом инвестиционный бюджет фирмы ограничен.
Пример 2.4
Фирма рассматривает возможность участия в финансировании шести проектов, предполагаемые условия реализации которых приведены в табл. 2 4. Инвестиционный бюджет фирмы равен 250 000 ден.ед.
Перейдите на Лист6 и переименуйте его в Проекты A-F. Создайте шаблон таблицы 2.4.
Таблица 2.4. Условия реализации проектов для примера 2.4
| Прогкт | I | PV | NPV | PI |
| A | -80 000,00 | 95 000,00 | ||
| B | -60 000,00 | 79 000,00 | ||
| C | -70 000,00 | 112000,00 | ||
| D | -100 000,00 | 145 000,00 | ||
| E | -40 000,00 | 52 000,00 | ||
| F | -110000,00 | 126 500,00 |
Для расчета NPV=PV‑I введите в соответствующие ячейки формулы. Также введите формулы для расчета PI=PV/I в соответствующие ячейки. Результаты сравните с таблицей 2.4.1.
Таблица 2.4.1 Условия реализации проектов для примера 2.4
| Прогкт | I | PV | NPV | PI |
| A | -80 000,00 | 95 000,00 | 15 000,00 | 1,19 |
| B | -60 000,00 | 79 000,00 | 19 000,00 | 1,32 |
| C | -70 000,00 | 112000,00 | 42 000,00 | 1,60 |
| D | -100 000,00 | 145 000,00 | 45 000,00 | 1,45 |
| E | -40 000,00 | 52 000,00 | 12 000,00 | 1,3 |
| F | -110000,00 | 126 500,00 | 16 500,00 | 1,15 |
Как видим по данным табл. 2.4.1, все проекты имеют положительную NPV и, если бы инвестиционный бюджет фирмы не был ограничен суммой в 250 000 ден.ед., их следовало бы принять. Однако в силу ограниченности бюджета может быть реализован только тот набор (портфель) проектов, при котором суммарные инвестиции не превышают 250 000 ден.ед.
В данном случае существует несколько таких портфелей, поэтому возникает проблема выбора наиболее эффективной комбинации проектов. В условиях ограниченного бюджета наиболее эффективен (оптимален) для фирмы такой портфель проектов, который обеспечивает наибольшую отдачу вложенных средств и в конечном результате генерирует максимальную NPV.
Оптимальный портфель инвестиций в подобных условиях можно получить путем последовательного включения проектов в порядке убывания индексов рентабельности и проверки соблюдения ограничений.
Расположим проекты, приведенные в табл. 2.4, в порядке убывания индексов рентабельности (выполните сортировку данных по убыванию значений в поле PI). Добавьте столбец и рассчитайте NPV нарастающим итогом. Результаты представлены в таблице 2.5.
Та блица 2.5. Классификация проектов по индексам рентабельности
| Проект | I | PV | NPV | PI | NPV нарастающим итогом |
| С | -70 000,00 | 112000,00 | 42 000,00 | 1,60 | 42 000,00 |
| D | 100000,00 | 145 000,00 | 45 000,00 | 1,45 | 87 000,00 |
| В | -60 000,00 | 79 000,00 | 19 000,00 | 1,32 | 106 000,00 |
| Е | -40 000,00 | 52 000,0,0 | 12000,00 | 1,3 | 118000,00 |
| А | -80 000,00 | 95 000,00 | 15000,00 | 1,19 | 132000,00 |
| F | -•100000,00 | 126 500,00 | 16 500,00 | 1,15 | 148500,00 |
Как видим по данным из табл. 2.5, оптимальный в этих условиях портфель инвестиций будет состоять из проектов С, D и В. При этом суммарная NPV портфеля равна:
NPV =NPV(C) + NPV(D) + NPV(B) = 106 000,00 ден.ед.
Более эффективное решение подобных проблем может быть получено при использовании методов математического программирования и рассмотрено ниже.
Индекс рентабельности не всегда обеспечивает однозначную оценку эффективности инвестиций, и проект с наиболее высоким PI может • не соответствовать проекту с наиболее высокой NPV. В частности, использование индекса рентабельности может привести к ошибочным результатам при оценке взаимоисключающих проектов. Рассмотрим следующий пример.
Пример 2.5
Фирма рассматривает возможность участия в финансировании двух взаимоисключающих проектов, предполагаемые условия реализации которых приведены в табл. 2.6. Принятая норма дисконта для проектов одинакова и равна 10%. Необходимо выбрать наиболее эффективный проект инвестиций. На Листе7 сделайте расчеты как показано в таблице 2.6.
Таблица 2.6. Потоки платежей проектов (пример 2.5)
| Пр оект | I | CF1 | CF2 | РV | NPV |
| -100,00 | 200,00 | 250,00 | 388,43 | 288,43 | |
| -10 000,00 | 15 000,00 | 25 000,00 | 34 297,52 | 24 297,52 |
Определим индексы рентабельности для проектов 1 и 2:
PI1 = 388,43 / 100,00 = 3,88;
Р12 = 34 927,52 / 10 000,00 = 3,43.
Нетрудно заметить, что при наличии у фирмы соответствующих средств второй проект предпочтительнее, так как он генерирует большую NPV. Однако индекс рентабельности "отдает" предпочтение первому проекту.
Обычно расчет индекса рентабельности дополняет расчет NPV с целью отбора проектов, порождающих максимальную современную стоимость на единицу затрат.