В ППП EXCEL для расчета внутренней нормы доходности реализованы три функции — ВСД(), МВСД () и ЧИСТВНДОХ (). Функции используют следующие аргументы:
платежи — значения элементов денежного потока;
ставка — норма дисконта (процентная ставка);
ставка_реин — ставка реинвестирования (только для МВСД ());
даты — даты платежей (только для ЧИСТВНДОХ ());
прогноз — норма приведения (необязательный аргумент).
Для корректной работы этих функций денежный поток должен состоять из хотя бы одного отрицательного и одного положительного элемента (т.е. должны иметь место хотя бы одна выплата и одно поступление средств).
Функция ВСД (платежи; [прогноз])
Эта функция осуществляет расчет IRR по формуле (2.6) для денежного потока, заданного аргументом платежи.
Рассчитаем внутреннюю норму доходности для примера 2.1. Для этого введите в ячейку В18 формулу (рис. 2.7):
=ВСД(В10:В16) (Результат: 0,26 или 26%).

Рис. 2.7. Расчет внутренней нормы доходности (ВСД ())
Поскольку полученный результат превышает норму дисконта (10%), критерий IRR также рекомендует принять данный проект. При этом эффективность данной операции составит: 26% — 10% = 16%.
Используя полученную таблицу, самостоятельно проведите анализ чувствительности данного показателя к изменениям нормы дисконта и структуры потока платежей.
Функция ЧИСТВНДОХ(платежи; даты; [прогноз])
Функция ЧИСТВНДОХ () позволяет определить показатель IRR для потока платежей с произвольным распределением во времени, если известны их предполагаемые даты. Эту функцию удобно использовать в тандеме с функцией ЧИСТНЗ().
Модифицируем в очередной раз таблицу для решения примера 2.1. Введите в ячейку В19 формулу (рис. 2.8):
=ЧИСТВНДОХ (В10:В16; А10:А16) (Результат: 26%).
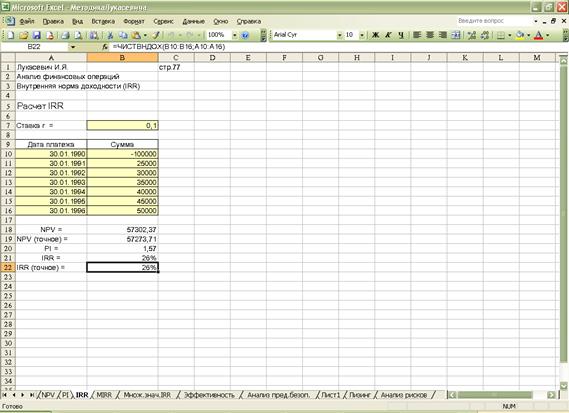
Рис. 2.8. Расчет внутренней нормы доходности (ЧИСТНЗ())
Показатель IRR, рассчитываемый в процентах, более удобен для применения в анализе, чем показатель NPV^ поскольку относительные величины легче поддаются интерпретации. Например, эффективность проекта с IRR = 26% очевидна для рассматриваемого примера, если необходимые для его реализации денежные средства можно занять в банке под 10% годовых.
Критерий внутренней нормы доходности несет в себе также информацию о приблизительной величине предела безопасности для проекта. Если предположить, что в предыдущем случае при оценке денежного потока возможна ошибка и IRR проекта окажется равной 20%, при прежней процентной ставке по кредиту (10%) проект все равно обеспечит получение дохода.
При повышении стоимости займа до 22 — 24% при IRR = 26% остается слишком малый предел безопасности на случай ошибки и, возможно, такой проект будет сразу отвергнут и проведение дальнейшего анализа не потребуется. Как показано ниже, ППП EXCEL позволяет быстро и эффективно осуществить анализ предела безопасности для инвестиционных проектов.
Рассмотренные достоинства критерия IRR объясняют его популярность на практике. Исследования зарубежного опыта показывают, что более 40% фирм используют этот критерий для оценки эффективности инвестиций [27, 28].
Вместе с тем его недостатки также требуют серьезного рассмотрения. К одному из наиболее существенных следует отнести нереалистичное предположение о ставке реинвестирования.
В отличие от NPV критерий внутренней нормы доходности неявно предполагает реинвестирование получаемых доходов по ставке IRR. Если финансирование проекта в примере 2.1 осуществляется за счет банковской ссуды под 10% годовых, то получаемые в процессе его реализации доходы должны быть реинвестированы по ставке 26% годовых, т.е. в 2,6 раза превышающей ставку по долгосрочным кредитам! Очевидно, что это вряд ли осуществимо в реальной практике.
Для корректного учета предположения о реинвестировании в ППП EXCEL реализована функция МВСД().
Функция МВСД (платежи; ставка; ставка_реин)
Функция МВСД () вычисляет модифицированную внутреннюю норму доходности (modified internal rate of return — MIRR). Данная функция имеет специальный аргумент — предполагаемую ставку реинвестирования.
Предположим, что в примере 2.1 имеется возможность реинвестирования получаемых доходов по ставке 8% годовых. Тогда модифицированная внутренняя норма доходности, заданная в ячейке В23, составит (рис. 2.9):
=МВСД(В10:.В16; В7; В8) (Результат: 18%).

Рис. 2.9. Расчет внутренней нормы доходности (МВСД())
Нетрудно заметить, что полученная модифицированная норма рентабельности почти на треть ниже предыдущей, однако выше заданной, поэтому даже при более пессимистичной оценке реальных условий проект можно считать прибыльным.
Варьируя значение ставки реинвестирования, проследите изменения показателя MIRR.
Второй недостаток показателя внутренней нормы доходности связан с возможностью существования его нескольких значений.
В общем случае, если анализируется единственный или несколько независимых проектов с "обычным" денежным потоком (т.е. после первоначальных затрат следуют положительные притоки денежных средств), применение критерия IRR всегда приводит к тем же результатам, что и NPV.
Однако в случае чередования притоков и оттоков наличности (например, в случае капитального ремонта или модернизации оборудования) для одного проекта могут существовать несколько значений IRR. Объяснение этого факта следует из соотношения (2.6). Нетрудно заметить, что IRR является корнем функции NPV = f(r) = 0, которая в общем случае задается полиномом п-й степени, где п — число периодов реализации проекта. Согласно правилу Декарта, полином п-й степени может иметь столько корней, сколько раз меняет знак заданная им функция. Таким образом, уравнение NPV == f(r) == 0 имеет столько корней, сколько раз меняется знак потока платежей.
Пример 2.6
Фирма рассматривает возможность реализации проекта, генерирующего следующий денежный поток (табл. 2.7). Определить эффективность проекта, если норма дисконта равна 10%.
Таблица 2.7. Поток платежей проекта-из примера 2.6
| Период | to | t1 | t2 |
| Сумма | -1600 | -10000 |
Определим NPV для данного проекта:
-1600 + НПЗ(0,1; {10000; -10000}) (Результат:-773,55).
Проведенный расчет показывает, что критерий NPV рекомендует отклонить проект. Выполнив ряд преобразований над выражением (2.6), определим величину IRR:
NPV=0 = 1600(1+IRR)2 - 10000(1+IRR) + 10000.
Нетрудно заметить, что полученное соотношение является квадратным уравнением и имеет два корня:

откуда IRR1= 25% и IRR2=400%.
Моделирование зависимости NPV от нормы дисконта r, выполненное в среде ППП EXCEL для рассматриваемого примера, представлено на рис. 2.10.

Рис. 2.10. Множественные значения IRR
В этом случае принять однозначное решение на основе показателя IRR нельзя. Наиболее простое решение в такой ситуации — руководствоваться наименьшим значением IRR среди всех полученных.
К сожалению, функции ППП EXCEL также не всегда обеспечивают в таком случае получение правильного результата1. Можно попытаться найти приемлемое значение IRR варьированием значений необязательного аргумента прогноз (от 0,1 до 0,9).
Еще одним недостатком показателя IRR является то, что как и показатель PI, он не всегда позволяет однозначно оценить взаимоисключающие проекты.
Подводя итоги, отметим, что в целом метод NPV дает более достоверные результаты. Вместе с тем наиболее правильным подходом к анализу эффективности долгосрочных инвестиций будет применение всех рассмотренных показателей, так как различные способы оценки обеспечивают лиц, принимающих решения, более полной информацией.
Как показано в дальнейшем, применение ЭТ позволяет быстро и эффективно определить значения всех необходимых критериев оценки и провести анализ их чувствительности.
Пример 2.7
Фирма рассматривает возможность осуществления инвестиционного проекта, срок действия которого составляет 6 лет. Норма дисконта равна ставке реинвестирования и составляет 10%. Поток платежей по проекту представлен в табл. 2.10.
Т а б л и ц а 2.10. Поток платежей проекта (пример 2.7)
| Дата | 25.01.90 | 25.01.91 | 25.01.92 | 25.01.93 | 25.01.94 | 25.01.95 |
| Платеж | -1000 | -100 |
Определить значения критериев эффективности для проекта. Рассмотрим решение примера.
Полученная в результате таблица должна иметь вид, представленный на рис. 2.12.

Рис. 2. 72 Анализ эффективности проекта (пример 2.7)
Проведенный анализ показывает экономическую эффективность данного проекта, поэтому при отсутствии других альтернатив он может быть принят.
Необходимо запомнить
ü Анализ эффективности долгосрочных инвестиционных проектов является ключевым разделом финансового менеджмента. Принятые в этой области решения во многом предопределяют положение фирмы в будущем.
ü Количественные методы оценки эффективности инвестиций можно разбить на две группы — статические и динамические. Последние также называют дисконтными, поскольку они базируются на исчислении современной стоимости (дисконтировании) потоков платежей, возникающих в процессе реализации проектов.
ü Дисконтные методы позволяют учесть фактор времени в процессе реализации инвестиционных проектов. Наиболее часто используются из них: метод чистой современной стоимости (net present value — NPV)\ метод индекса рентабельности (profitability index — Р7); метод внутренней нормы доходности (internal rate of return - IRR, MIRR).
ü В процессе анализа следует использовать все три метода оценки. Однако при анализе взаимоисключающих проектов применение критериев NPV, IRR, PI может привести к различным результатам. В этом случае следует отдать предпочтение методу NPV.
ü Наиболее достоверным методом оценки является метод NPV. Вместе с тем его применение не всегда удобно, так как абсолютные величины труднее поддаются интерпретации.
ü Наиболее популярным методом оценки является метод IRR. К числу наиболее существенных недостатков этого метода следует отнести: некорректность предположения о ставке реинвестирования средств (устраняется путем расчета критерия MIRR); возможность получения нескольких значений для нестандартных потоков платежей; возможность принятии неправильного решения при оценке взаимоисключающих проектов.
ü Современные табличные процессоры содержат специальные функции, позволяющие быстро и эффективно определить основные критерии эффективности инвестиций. В ППП EXCEL для этих целей следует использовать следующие функции нпз(), чистнз(), вндох(), чиствндох, мвсд().
ü Применение методов математического программирования часто обеспечивает получение оптимальных результатов в условиях ограниченных ресурсов. В ППП EXCEL для этих целей следует использовать специальный инструмент — Поиск решения.
ü Применение табличных процессоров при решении подобных задач позволяет автоматизировать проведение расчетов, а также осуществить их моделирование, существенно повышая эффективность анализа и достоверность его результатов.
Вопросы для самоконтроля
1. Почему анализ эффективности долгосрочных инвестиций считают ключевым разделом финансового менеджмента?
2. Какой признак положен в основу классификации показателей эффективности инвестиций?
3. Назовите известные вам показатели эффективности инвестиций. Дайте характеристику каждому показателю, приведите формулы для их исчисления.
4. Назовите основные факторы, оказывающие существенное влияние на показатель NPV.
5. В каких случаях возможно появление нескольких значений IRR?
6. Для чего необходим анализ показателей на чувствительность?
7. В каких случаях показатели PI и IRR могут противоречить показателю NPV?
8. Какой из показателей эффективности инвестиций получил наиболее широкое распространение? Почему?
9. При анализе взаимоисключающих проектов "А" и "Б" были получены следующие результаты: IRR(A) = 15%, IRR(B) = 12%, NPV(A) = 10000, NPV(B) =12500. Норма дисконта для обоих проектов одинакова и равна 9%. Какой проект вы предпочтете? Почему?
10. Анализ двух независимых проектов показал, что они имеют почти равную NPV. Как вы поступите в этой ситуации?
11. Назовите финансовые функции ППП EXCEL, предназначенные для анализа эффективности долгосрочных инвестиций. Приведите их форматы и примеры задания.
12. В чем заключаются преимущества применения ЭТ при анализе эффективности инвестиционных проектов?
Задачи и упражнения
Используя разработанные ранее таблицы-шаблоны, выполните следующие упражнения.
Задача 1. Реализация проекта, предусматривающего затраты в размере 60 000 ден. ед., должна дать чистый поток наличности, имеющий следующую структуру: 10000, 15000, 15000, 20000, 15000, 10000, 5000. Определите:
а) NPV, PI, IRR для этого проекта при норме дисконта 10% и 15%;
б) NPV, PI, IRR при условии, что притоки денежной наличности одинаковы и составляют 13 000 ден.ед. Нормы дисконта прежние;
в) как изменятся NPV, PI, IRR, если последний приток наличности возрастет до 10 000 ден.ед.; снизится до 2 000?
Задача 2. Фирма рассматривает возможность финансирования трех проектов, денежные потоки которых представлены в таблице:
| Период | Проект Y | Проект Z | Проект W |
| -20 000,00 | -130000,00 | -100 000,00 | |
| 15000.00 | 80 000.00 | 90 000,00 | |
| 15 000,00 | 60 000,00 | 30 000,00 | |
| 15000,00 | 80 000,00 |
Определите:
a) NPV, PI, IRR для этих проектов при норме дисконта 15%. Какой из проектов вы предпочтете? Почему?
Задача 3. Корпорация "К" рассматривает два взаимоисключающих инвестиционных проекта. Структуры денежных потоков для проектов представлены в таблице:
| Период | Проект X | Проект S |
| -400,00 | -200,00 | |
| 241,00 | 131.00 | |
| 293,00 | 172,00 |
Норма дисконта для обоих проектов одинакова и равна 9%. Какой из проектов вы предпочтете? Почему?
Задача 4. Поток платежей по проекту "G" имеет структуру, приведенную в таблице:
| Период | ||||||
| Платежи | -1000 | -100 | -400 |
Определите внутреннюю норму доходности для этого проекта с использованием функций ВНДОХ() и МВСД(). Объясните полученные результаты.
Задача 5. Проекты "А" и "Б" требуют одинакового объема первоначальных инвестиций — 5000 ден.ед. Без учета дисконтирования проект "А" генерирует поток платежей, равный 12000, а проект "Б" - 10 000 ден.ед. После дисконтирования потоков платежей по норме г= 10% оба проекта имеют равную NPV.
У какого проекта величина NPV будет более чувствительна к изменению нормы дисконта? Подкрепите свои рассуждения графическими иллюстрациями.
Задача 6. Фирма рассматривает два взаимоисключающих проекта "Т" и "С", генерирующих следующие потоки платежей:
| Период | |||||
| Проект "Т" | -2000 | ||||
| Проект "С" | -2000 |
Стоимость капитала для фирмы составляет 9%. Определите критерий IRR для каждого проекта. Можно ли в данном случае принять решение, основываясь только на критерии IRR? Какой проект вы рекомендуете принять? Почему?
7. Отчет по лабораторной работе должен содержать:
1. Ответы на вопросы для самоконтроля
2. Таблицы с решениями задач 1-6 с выводами о целесообразности принятия проекта(ов).