Конструкции арок. Арочные системы имеют давнюю историю. Многочисленные своды, дошедшие до сегодняшних дней – яркое тому подтверждение. Стержневая система, состоящая из криволинейного стержня, разделенного шарниром, называется трехшарнирной аркой. Это статически определимая геометрически неизменяемая система, которая широко используется в настоящее время. Строительная арочная конструкция является надежной и рациональной, она способна перекрывать большие пролеты, используется в мостостроении и в качестве покрытий большепролетных сооружений (спортивных залов, кинотеатров и т.д.). При вертикальной нагрузке в опорах арки возникают горизонтальные реакции. Поэтому трехшарнирные арки относят к распорным системам.
Трехшарнирная рама с опорами в одном уровне изображена на рис. 8.14,а. Наиболее важными характеристиками арки являются ее пролет l и стрела подъема f. Средний шарнир называется ключом или замком арки. Арка может также иметь опоры в разных уровнях. На рис. 8.14, б представлена трехшарнирная рама с затяжкой, расположенной выше опор на расстоянии t. Затяжка также бывает в одном уровне с опорами (не представлена на этом рисунке). Арка с затяжкой как бы замкнута сама на себя. Затяжка работает на растяжение при наличии вертикальных нагрузок и может быть выполнена из гибкого троса. Конструкции, изображенные на рис. 8.14 в, г не могут быть отнесены к категории арок, так как при действии вертикальной нагрузки в них не возникает горизонтальных реакций (распора) в опорах. Наиболее распространенными формами арки являются круговая и параболическая.
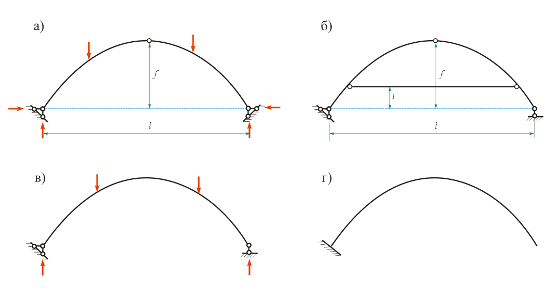
Рис. 8.14. Криволинейные стержневые системы
Расчет арок. Рассмотрим вначале трехшарнирную арку с опорами в одном уровне, загруженную только вертикальной силой P, приложенной в шарнире (рис. 8.15). Очевидно, что вертикальные реакции равны P /2 (их можно найти как в обычной балке на двух опорах). Чтобы определить правую горизонтальную реакцию, найдем изгибающий момент в шарнире
|
|
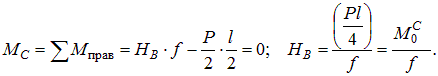
Из суммы проекций сил на горизонтальную ось следует, что горизонтальные реакции равны, то есть 
.
Величиной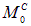 
обозначен балочный момент в т. С, то есть, для того, чтобы найти распор, нужно представить арку в виде балки на двух опорах, вычислить момент в т. С, а затем разделить его на стрелу подъема f. Это утверждение для данной арки можно распространить и на другие арки с другой нагрузкой. Получаем формулу для определения распора в трехшарнирной арке без затяжки.
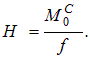
| (8.6) |
На рис. 8.15 показана балочная эпюра изгибающих моментов M 0 и конечная эпюра моментов M в арке (приведем ее без расчетов). Она имеет криволинейный характер.
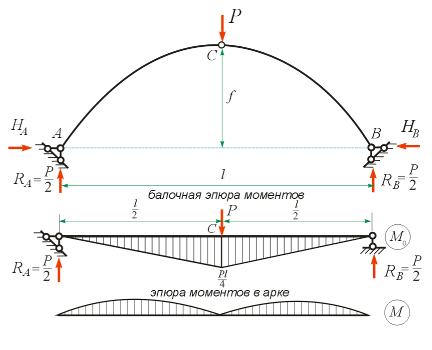
Рис. 8.15. К определению величины распора
Рассмотрим, как можно определить внутренние усилия в произвольной точке арки с координатами x и y, представленной на рис. 8.16.
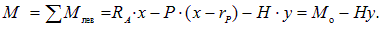
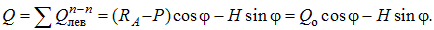
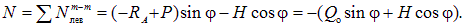
| (8.7) |
В первой строке (8.7), смысл которой состоит в определении изгибающего момента в произвольной точке, как момента левых сил, выражение 
представляет собой изгибающий момент в балке на двух опорах с тем же пролетом, что и арка, в точке с координатой х (балочный момент M o).
Во второй строке (8.7), которая представляет собой сумму проекций левых сил на перпендикуляр n-n коси арки, выражение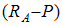 
является поперечной силой в балке на двух опорах с тем же пролетом, что и арка, в точке с координатой х (балочная поперечная сила Q o).
|
|
Третья строка (8.7) представляет сумму проекций левых сил на касательную m-m к оси арки к произвольной точке, а выражение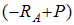 
является балочной поперечной силой Q o с обратным знаком.
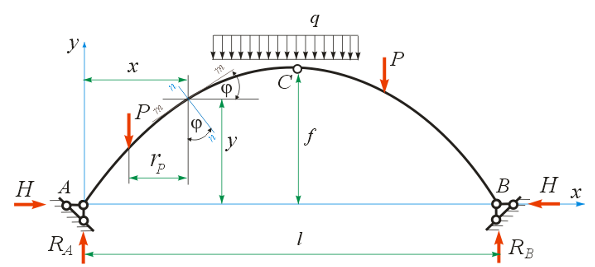
Рис. 8.16. К определению внутренних усилий в произвольном сечении арки
Итак, для арки без затяжки имеем следующие выражения для определения внутренних усилий в произвольном сечении арки
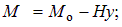
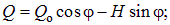
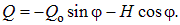
| (8.8) |
Рассмотрим арку с затяжкой (рис. 8.17)
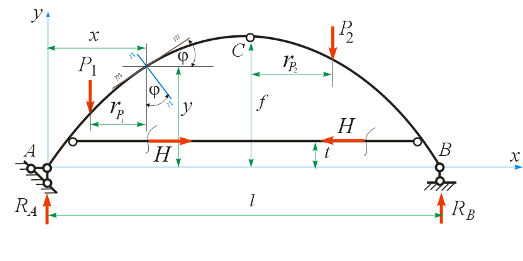
Рис. 8.17. К определению внутренних усилий в произвольном сечении арки с затяжкой
Вертикальные опорные реакции определяют, как в балке на двух опорах. Горизонтальная реакция равна нулю. Чтобы найти распор Н в затяжке, выполним ее сечение, а затем запишем сумму моментов правых сил в сечении С и приравняем ее нулю.
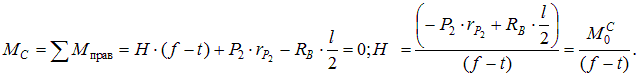
Выражение в числителе представляет собой балочный момент в точке С. Формула для определения распора в затяжке имеет вид.
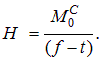
| (8.9) |
Внутренние усилия в трехшарнирной арке с затяжкой будут равны:
- для сечений ниже затяжки
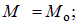
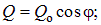
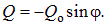
| (8.10) |
- для сечений выше затяжки
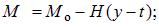
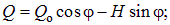
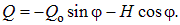
| (8.11) |
Отметим, что величины поперечной силы Q и изгибающего момента M в арке имеют значительно меньшие величины, чем для балки того же пролета (Q o и M o). Обратим также внимание, что в эпюре продольных сил N имеют место значительные величины сжимающих усилий.
Нормальные напряжения в сечении арки. Можно подсчитать нормальные напряжения в арке в любом сечении и сравнить их с предельными величинами, используя условие прочности:
|
|
 .
| (8.12) |
Условие прочности (8.12) основано на применении принципа суперпозиции. Первый член дает нам отрицательные напряжения от центрального сжатия, а второй – знакопеременные нормальные напряжения на крайних волокнах от изгиба. Как уже отмечалось, сжимающая сила N в арке достигает значительно больших величин, чем изгибающие моменты М. Поэтому первый член (8.12), зависящий от продольной силы, имеет значительно большую величину, чем второй член, содержащий изгибающий момент. Поэтому, суммарное нормальное напряжение в арке во всех сечениях будет сжимающим. Для материалов типа бетона или каменной кладки – это обстоятельство имеет решающее значение. Ведь конструкции из хрупких материалов практически не работают на растяжение. Древние строители интуитивно выбрали арочные конструкции, выполняя их из каменной кладки, так как они работают только на сжатие.
Рациональная ось арки. Решим задачу об отыскании такого очертания трехшарнирной арки без затяжки, загруженной равномерно распределенной нагрузкой q, чтобы в ней вообще не возникало изгибающих моментов. На рис. 8.22, а показано сечение арки с действующими внутренними силами. Для начала перенесем продольную силу N из точки С в точку D на такое расстояние e (его называют эксцентриситетом) от оси арки (рис. 8.22, б), чтобы она создавала относительно оси момент M=N× e. Тогда эксцентриситет e можно определить по формуле
 .
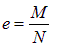| (8.14) |
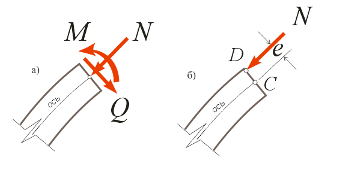
Рис. 8.22. Кривая давления проходит через точку D
Если бы арка была очерчена по точкам D в каждом сечении, то изгибающего момента во всех сечениях не существовало. Геометрическое место точек приложения равнодействующей в каждом сечении называется кривой давления. Если арка очерчена по кривой давления, в каждом сечении возникают равномерно распределенные по сечению нормальные напряжения сжатия.
Рациональной осью арки называется ее ось, очерченная по кривые давления.
Выясним, какая должна быть математическая функция рациональной оси трехшарнирной арки без затяжки, загруженной равномерно распределенной нагрузкой q. С некоторым приближением такой вариант имитирует загружение арки ее собственным весом.
Из первого равенства (8.8) имеем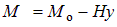 
. Откуда 
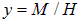. Из (8.6) имеем 
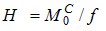, что позволяет получить выражение функции y (x)
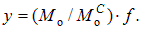
| (8.15) |
Для симметричной балки одинакового пролета l с аркой, загруженной равномерно распределенной нагрузкой q, балочный изгибающий момент в середине балки определяется по формуле
 .
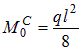| (8.16) |
Для такой же балки, учитывая, что опорные реакции равны ql /2, можно записать выражение функции зависимости балочного момента от х.
 .
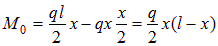| (8.17) |
Подставляя (8.16) и (8.17) в (8.15), получим
 .
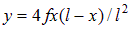| (8.18) |
Получили функцию квадратной параболы, график которой и будет изображать рациональную ось трехшарнирной арки, загруженной равномерно распределенной вертикальной нагрузкой. В такой арке не будет изгибающих моментов.