35. Экстремумы функции нескольких переменных. Опр: функция 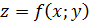 имеет max в точке
имеет max в точке  если f
если f 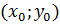 >
>  . Для всех точек
. Для всех точек  близких к точке
близких к точке  и отличных от нее. Опр: функция
и отличных от нее. Опр: функция 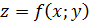 имеет min в точке
имеет min в точке  если f
если f 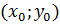 <
<  . Для всех точек
. Для всех точек  близких к точке
близких к точке  и отличных от нее. Необходимое условие экстремума: если функция достигает экстремума при x=
и отличных от нее. Необходимое условие экстремума: если функция достигает экстремума при x= 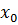 и y=
и y= 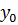 то каждая частная производная первого порядка или обращается в 0 при этих значениях или не существует. Достаточное условие экстремума: Пусть в некоторой области содержащей точку
то каждая частная производная первого порядка или обращается в 0 при этих значениях или не существует. Достаточное условие экстремума: Пусть в некоторой области содержащей точку  функция имеет непрерывные частные производные до третьего порядка включительно и пусть точка
функция имеет непрерывные частные производные до третьего порядка включительно и пусть точка  является критической точкой функции, то есть
является критической точкой функции, то есть 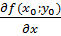 =0;
=0; 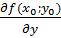 =0. Существуют следующие равенства: А=
=0. Существуют следующие равенства: А= 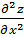 ; В=
; В= 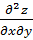 ; С=
; С= 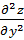 тогда при x=
тогда при x= 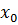 и y=
и y= 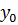 : 1. Если А*С-
: 1. Если А*С-  >0, А<0 то в точке
>0, А<0 то в точке  существует max. 2. Если А*С-
существует max. 2. Если А*С-  >0, А>0 то в точке
>0, А>0 то в точке  существует min. 3. Если А*С-
существует min. 3. Если А*С-  =0, то в точке
=0, то в точке  экстремум может быть, а может и не быть. 4.. Если А*С-
экстремум может быть, а может и не быть. 4.. Если А*С-  <0, то в точке
<0, то в точке  экстремума нет.
экстремума нет.
36. Касательная плоскость и нормаль к поверхности. Опр: Прямая линия называется касательной к поверхности в некоторой точке если она является касательной к какой либо кривой лежащей на поверхности и проходящей через данную точку. Через данную точку может проходить бесконечное число различных кривых лежащих на поверхности, то и касательных к поверхности проходящих через данную точку будет бесконечное множество. Опр: Если в точке 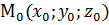 все три частные производные
все три частные производные 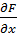 ;
;  ;
; 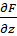 ; равны 0 или хотя бы одна их этих производных не существует, то точка
; равны 0 или хотя бы одна их этих производных не существует, то точка  называется особой точкой поверхности, в противном случае она называется обыкновенной точкой. Опр: Касательные прямые к данной поверхности в ее обыкновенной точке лежат в одной плоскости которая называется касательной плоскостью и имеет уравнение:
называется особой точкой поверхности, в противном случае она называется обыкновенной точкой. Опр: Касательные прямые к данной поверхности в ее обыкновенной точке лежат в одной плоскости которая называется касательной плоскостью и имеет уравнение: 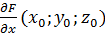 (х-
(х-  +
+ 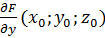 (
( )+
)+ 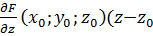 ). В особых точках касательная к плоскости может не существовать. Опр: прямая проведенная через данную точку поверхности перпендикулярную касательной плоскости называется нормалью. Уравнение нормали:
). В особых точках касательная к плоскости может не существовать. Опр: прямая проведенная через данную точку поверхности перпендикулярную касательной плоскости называется нормалью. Уравнение нормали: 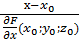 =
= 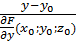 =
= 
37. Скалярное поле. Производная скалярного поля в заданном направлении. Градиент. Опр: Скалярное поле – это множество точек в которых задана скалярная функция, то есть функция значениями которой являются числа. Поле называется плоским если точки заданы на плоскости, и пространственным если точки заданы в пространстве. U=U  – плоское, U=U
– плоское, U=U  - пространственное. Опр: Линиями или поверхностями уровня скалярного поля называются линии или поверхности в точках которых поле принимает постоянное значение. U
- пространственное. Опр: Линиями или поверхностями уровня скалярного поля называются линии или поверхности в точках которых поле принимает постоянное значение. U 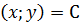 - линии уровня. U
- линии уровня. U  = С – поверхности уровня. Производная скалярного поля по направлению: опр: Производной скалярного поля в заданном направлении называется предел отношения величины изменения поля в этом направлении к расстоянию, когда расстояние стремится к 0.
= С – поверхности уровня. Производная скалярного поля по направлению: опр: Производной скалярного поля в заданном направлении называется предел отношения величины изменения поля в этом направлении к расстоянию, когда расстояние стремится к 0.  =
= 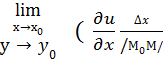 +
+ 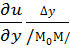 + α
+ α 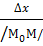 +β
+β  =
= 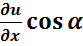 +
+  ,
,  , М(x; y). Производная пространственного поля:
, М(x; y). Производная пространственного поля:  =
= 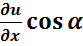 +
+  +
+ 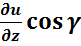 . Определение градиента: вектор
. Определение градиента: вектор 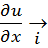 +
+  +
+ 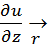 называется grad скалярного поля U(M) в точке М(x; y; z). grad U(M)=
называется grad скалярного поля U(M) в точке М(x; y; z). grad U(M)=  +
+  +
+ 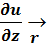
38. Определение первообразной и неопределенного интеграла. Геометрический смысл. Опр: функция F(x) называется первообразной для функции f(x) на промежутке (а;в) если во всех точках этого промежутка выполняется равенство F(x)= f(x). Теорема(основное свойство первообразной): если функция имеет первообразную то все другие первообразные отличаются от нее только на произвольную постоянную, то есть если F(x) – первообразная для f(x), то существует Ф(x) = F(x)+ с. Доказательство: если F'(x)= f(x) пусть существует другая первообразная Ф(x), тогда по определению Ф'(x)= f(x).(Ф(x)- F(x))' = Ф'(x)- F'(x)= f(x)- f(x)=0↔ Ф(x)- F(x) = с, с- const. Ф(x)= F(x) + с. Опр: Неопределенным интегралом функции называется все множество первообразных этой функции. 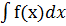 = F(x)+ с. Геометрически неопределенный нтеграл представляет собой семейство кривых, каждая из которых получается путем сдвига одной кривой параллельно самой себе вверх или вниз вдоль оси y.
= F(x)+ с. Геометрически неопределенный нтеграл представляет собой семейство кривых, каждая из которых получается путем сдвига одной кривой параллельно самой себе вверх или вниз вдоль оси y.