Ситуационная (практическая) задача № 2

Ситуационная (практическая) задача № 1

 

Время x (в мин.) между прибытием двух автомашин к светофору является случайным с плотностью распределения

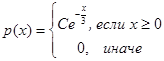
§ Установить неизвестную постоянную С и построить график функции p(x)

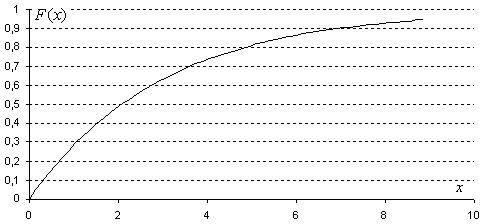
§ Найти функцию распределения случайной величин x и построить ее график

§ Вычислить математическое ожидание (среднее значение), дисперсию и среднее квадратическое (стандартное) отклонение рассматриваемой случайной величины

§ Во сколько раз число прибывших к светофору автомашин со временами между прибытиями больше среднего превосходит число автомашин со временами между прибытиями меньше среднего?

Решение:

1. Находим С из условия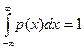

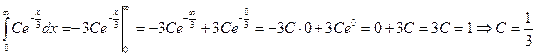
Плотность распределения случайной величин x:

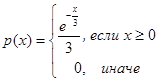
График функции p(x)

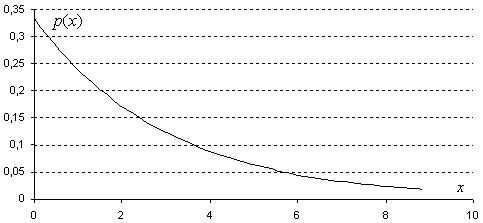
2. функцию распределения случайной величин x:

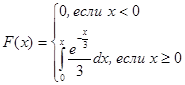
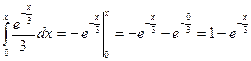
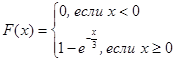
График функции F(x)

Математическое ожидание:

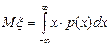
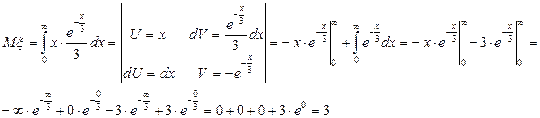
Дисперсия:

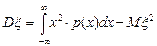
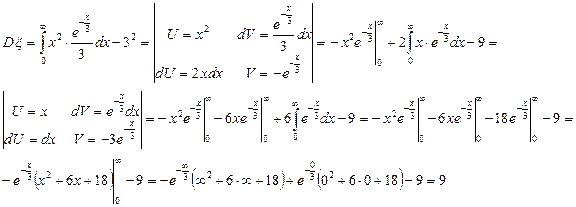
Среднее квадратическое (стандартное) отклонение:

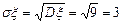
Доля автомашин со временами между прибытиями меньше среднего:

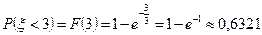
Доля автомашин со временами между прибытиями больше среднего:

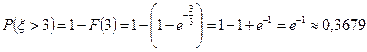
Число прибывших к светофору автомашин со временами между прибытиями больше среднего превосходит число автомашин со временами между прибытиями меньше среднего 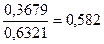раз.

Ситуационная (практическая) задача № 2

 

При измерении веса 25 упаковок сильнодействующего лекарственного препарата были обнаружены следующие отклонения (в гр.) от указанного на обертке:

–24,34; –14,59; –18,27; –8,94; –15,09; –10,94; 4,47; 3,05; –8,33; –22,98; 1,75;

–32,07; –7,43; –18,63; –12,97; –11,08; –7,44; –1,70; 6,34; –11,08; –11,12; –15,90;

–10,26; –8,07; –6,48.

Необходимо:

§ Определить исследуемый признак и его тип (дискретный или непрерывный).

§ В зависимости от типа признака построить полигон или гистограмму относительных частот.

§ На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.

§ Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение.

§ Используя критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в п.3 закону распределения при уровне значимости 0,05.

§ Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,95.

§ С надежностью 0,95 проверить гипотезу о равенстве:

а) генеральной средней значению –10;

б) генеральной дисперсии значению 100.

Решение:

1. Тип признака непрерывный, т.к. исходные цифры могут принимать любые дробные значения на определенном промежутке.

Разобьем данные на 5 равных интервалов:

Длина интервала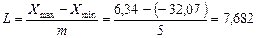

Интервал

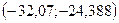
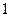
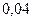
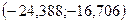
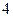
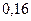
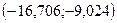
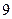
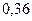
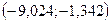
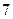
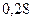
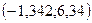
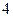
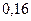
Гистограмма относительных частот

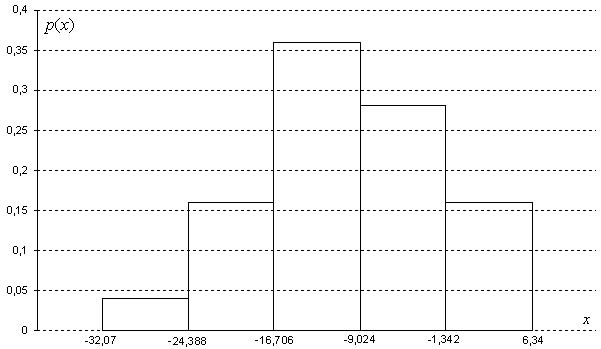
3. На основе анализа гистограммы распределения выдвигаем гипотезу о нормальном законе распределения исследуемого признака.

4. Среднее значение:

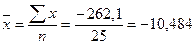
Дисперсия:

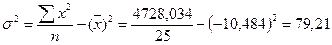
Среднее квадратическое (стандартное) отклонение:

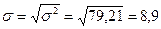
5. Вводим гипотезы:

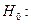Исследуемый признак имеет нормальное распределение:

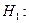Исследуемый признак имеет другое распределение:

Условие принятия гипотезы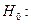

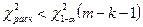
Вероятность попадания в интервалы:

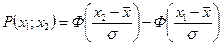
Интервал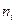
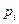
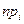
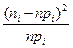
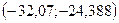
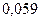
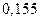
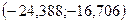
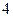
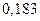
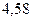
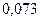
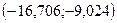
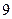
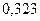
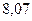
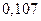
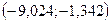
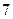
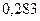
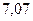
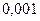
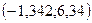
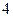
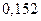
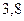
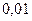
Сумма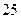

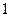
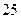
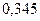
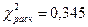
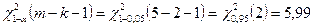
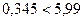, следует гипотезу о нормальном распределении исследуемого признака принимаем, при доверительной вероятности 95%.

 

6. Доверительный интервал для генерального среднего, при доверительной вероятности 95%:

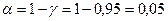
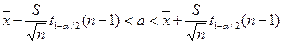
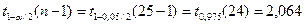
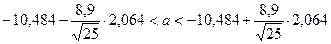
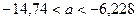
С вероятностью 95% генеральное среднее находится в интервале от 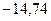до .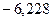

Доверительный интервал для генеральной дисперсии, при доверительной вероятности 95%:

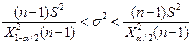
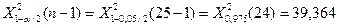
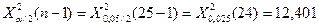
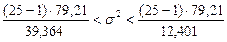
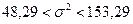
С вероятностью 95% генеральная дисперсия находится в интервале от 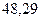до .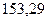

7а. Вводим гипотезы:

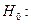
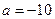
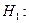
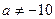
Условие принятия гипотезы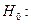

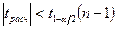
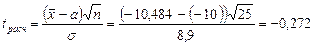
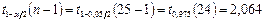
Условие принятия гипотезы выполняется 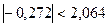, следует с вероятностью 95% генеральное среднее можно считать равным -10.

7б. Вводим гипотезы:

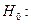
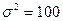
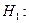
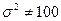
Условие принятия гипотезы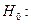

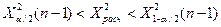
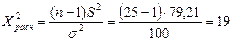
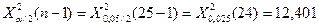
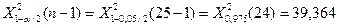
Условие принятия гипотезы выполняется 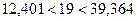, следует с вероятностью 95% генеральную дисперсию можно считать равной 100.

Тестовые задания

Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.

1. Студент знает 12 вопросов программы по теории вероятностей и математической статистике из 20. На зачете ему предлагается три наудачу выбранных из программы вопроса. Найти вероятность того, что студент ответит хотя бы на один вопрос.

А. 0,9509

Б. 0,4632

В. 0,007

Г. 0,0591

 

2. Охотник стреляет три раза по удаляющейся цели. Вероятность попадания в цель в начале стрельбы равна 0,9, а после каждого выстрела уменьшается на 0,15. Найти вероятность того, что охотник попадет ровно один раз.

А. 0,405

Б. 0,45

В. 0,135

Г. 0,01

 

3. На складе находятся одинаковые изделия, изготовленные тремя заводами: первым заводом произведено 35% всех изделий, вторым – 45%, а остальные изделия с третьего завода. Известно, что из каждой сотни изделий удовлетворяют стандарту в среднем 90 изделий, изготовленных на первом заводе, 85 – на втором, 60 – на третьем. Для контроля качества наудачу берется одно изделие. Найти вероятность того, что это изделие окажется стандартным?

А. 0,315

Б. 0,3825

В. 0,12

Г. 0,8175

4. Магазин торгует телевизорами двух марок А и В, пользующихся одинаковым спросом населения. За день торговли из имеющихся 4 телевизоров марки А и 6 телевизоров марки В было продано два телевизора. На следующий день магазин получил 2 телевизора А и 4 телевизора марки В. За второй день торговли продали один телевизор, который оказался марки А. Какова вероятность, что в первый день были проданы телевизоры марки В?

А. 0,3846

Б. 0,5128

В. 0,1026

Г. 0,3714

 

5. Из-за болезни на работу ежедневно не выходит в среднем 10% работников предприятия. Какова вероятность того, что из 4 работников, выбранных наудачу из списочного состава предприятия, на работе будет присутствовать ровно 3 сотрудника предприятия?

А. 0,2916

Б. 0,7084

В. 0,0036

Г. 0,9964

 

6. В среднем 25% пакетов акций на аукционе продаются по первоначально заявленной цене. Какова вероятность того, что из 6 наугад взятых пакетов акций будет продано по первоначально заявленной цене хотя бы 3?

А. 0,8306

Б. 0,1694

В. 0,0376

Г. 0,9624

 

7. Согласно статистическим данным в городе N в среднем 24% открывающихся новых предприятий прекращают свою деятельность в течение года. Какова вероятность, что из четырехсот наугад выбранных новых предприятий к концу года деятельности останется не менее 90, но не более 100 предприятий?

А. 0,439

Б. 0,2412

В. 0,6802

Г. 0,1802

 

8. При социологических опросах города N установлено, что в среднем 19% дают неискренний ответ. Сколько нужно опросить граждан города N, чтобы с вероятностью 0,94 можно было утверждать, что доля неискренних ответов среди них отклонится по абсолютной величине от вероятности получения неискреннего ответа от каждого опрашиваемого не более, чем на 0,02.

А. 1360

Б. 37

В. 15

Г. 94

 

9. Из поступивших в ремонт пяти часов три нуждаются в общей чистке механизма. Часы не рассортированы по виду ремонта. Мастер, желая найти часы, нуждающиеся в чистке, рассматривает их поочередно и, найдя такие часы, прекращает дальнейший просмотр. Найти математическое ожидание и дисперсию числа просмотренных часов.

А.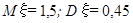

Б.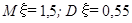

В.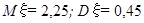

Г.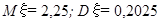

 

10. Для сигнализации об аварии в офисе некоторой фирмы города N установлено три сигнализатора различных типов, которые работают независимо друг от друга. Во время аварии сигнализаторы первого типа не срабатывают в среднем в 10%, второго – 8%, третьего 15% всех аварийных случаев. Рассматривается случайная величина 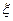- число сработавших сигнализаторов во время аварии. Найти .

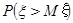А. 0,2962

Б. 0,7038

В. 0,2636

Г. 0,0314