Булевы функции и способы их задания

 

Под булевой функцией f (x ₁, x ₂, …, x_n) от n аргументов понимают функцию, которая на каждом n- мерном двоичном векторе (x ₁, x ₂, …, x_n) принимает определенное значение: либо 0, либо 1.

Задать булеву функцию f (x ₁, x ₂, …, x_n) – значит указать значение функции для каждого двоичного вектора (x ₁, x ₂, …, x_n). Можно доказать, что число таких векторов равно 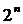. Следовательно, функцию f (x ₁, x ₂, …, x_n) можно задать с помощью таблицы, содержащей 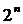строк и (n +1) столбцов. В первых n столбцах записывают все наборы значений аргументов, в (n +1) – соответствующие значения функции.

Ниже приведена таблица всех булевых функций от 2 аргументов:

 

x 1

x 2

x 1¯ x 2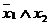

 

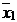
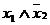
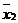
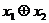
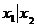
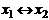
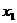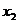
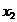
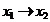
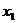
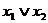
Обратим внимание на порядок расположения наборов значений независимых переменных x ₁и x ₂ в таблице: они образуют последователь­ности целых чисел, начиная с 0, записанных в двоичной системе счисления. Такой порядок записи называют лексикографическим порядком

В таблицу вошли отрицание, конъюнкция, дизъюнкция, сложение по модулю 2, две постоянные функции 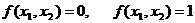, а также ряд других функций.

В теоретических курсах доказывается, что любую булеву функцию от любого числа аргументов можно записать в виде формулы, содержащей обозначения ее аргументов либо их отрицаний, соединенных знаками конъюнкции и дизъюнкции. Такое формульное задание функции называют совершенной дизъюнктивной нормальной формой (СДНФ) этой функции. Возможно также представление функции формулой, в которой используются операции сложения по модулю два, конъюнкция и булева константа 1. Такое представление называют полиномом Жегалкина.

Не вдаваясь в теорию, рассмотрим алгоритмы нахождения СДНФ и полинома Жегалкина и построения на их основе схем логических элементов реализующих заданный сигнал на выходе.

 

Пример.

На вход логической схемы подаются сигналы 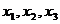, принимающие значения 0 или 1, с выхода необходимо снять сигнал y. Сигналы заданы в виде последовательности импульсов:

 

 

 

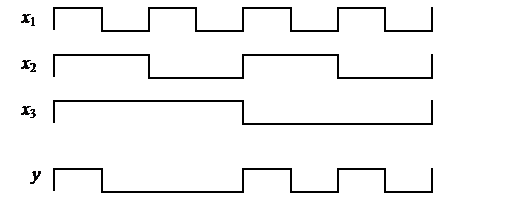Требуется:

1. Составить таблицу функции .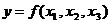

2. Составить СДНФ и полином Жегалкина функции y и упростить их.

3. Составить схему логического устройства, реализующего функцию y, на элементах: а) И, ИЛИ, НЕ, б) 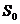, И, 1.

 

Р е ш е н и е.

 

1.

x 1	x 2	x 3	y		Дизъюнкты
				+
				+
				+

 

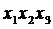
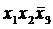
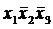
2. Составим СДНФ функции. Для этого надо:

1) Пометить все строки таблицы, в которых значение функции рав­но 1.

2) Для каждой из помеченных строк построить дизъюнкты, пред­ставляющие собой набор символов аргументов или их отрицаний, со­единенных знаками конъюнкции. Если значение аргумента в строке равно 1, то в дизъюнкт входит сам аргумент; если 0, то его отрица­ние.

3) Все построенные дизъюнкты соединить знаками дизъюнкции:

y =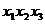

 

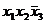
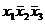
Полученная формула является СДНФ функции y.

Упростим СДНФ, пользуясь свойствами входящих в нее операций:

 

y = = = = =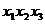

= = .

 

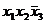
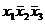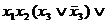
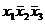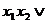
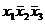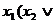
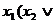
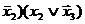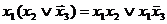Заменим операции дизъюнкция и отрицание операциями сложения по модулю 2:

y = = =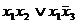

= = .

 

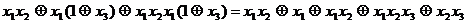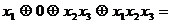
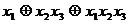3.

 

Отметим, что если большинство значений функции равно 1, то удобнее построить СДНФ для ее отрицания, а затем, применив отрицание к самой СДНФ получить нужную функцию.

 

Пример.

На вход логической схемы подаются сигналы 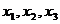, принимающие значения 0 или 1, с выхода необходимо снять сигнал y. Сигналы заданы в виде последовательности импульсов:

 

 

 

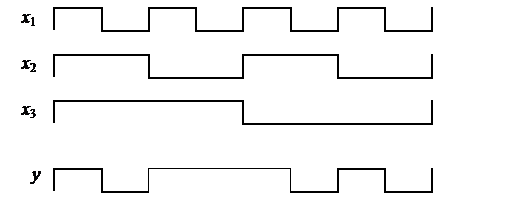
Требуется:

1. Составить таблицу функции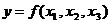

2. Составить СДНФ и полином Жегалкина функции y и упростить их.

3. Составить схему логического устройства, реализующего функцию y.

 

Р е ш е н и е.

 

1.

x 1	x 2	x 3	y		Дизъюнкты
				+
				+
				+

 

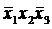
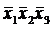
2. Составим СДНФ функции. Для этого надо:

1) Пометить все строки таблицы, в которых значение функции рав­но 1, но так как большинство значений функции равно 1, то удобнее построить СДНФ для ее отрицания, то есть пометим все строки в которых значения функции равно 0.

2) Для каждой из помеченных строк построить дизъюнкты, пред­ставляющие собой набор символов аргументов или их отрицаний, со­единенных знаками конъюнкции. Если значение аргумента в строке равно 1, то в дизъюнкт входит сам аргумент; если 0, то его отрица­ние.

3) Все построенные дизъюнкты соединить знаками дизъюнкции, а затем, применим отрицание ко всей функции, так как в п.2.1. строилась СДНФ для отрицания функции:

 

.

 

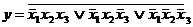Полученная формула является СДНФ функции y.

Упростим СДНФ, пользуясь свойствами входящих в нее операций:

= = = = = = = = = = = .

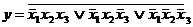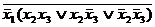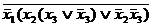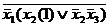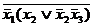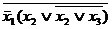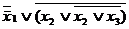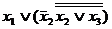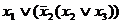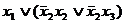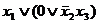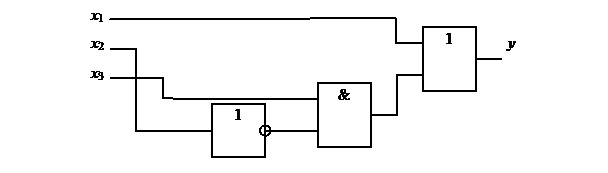
3.

 

Пример. Дана булева функция: .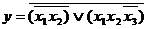

Требуется:

1. Упростить формулу, исключив фиктивные переменные.

2. Начертить схему, реализующую эту функцию.

 

Р е ш е н и е.

 

1. = =

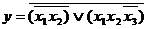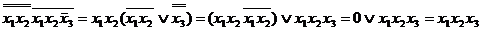
2.