Из книги И.Я. Депмана, Н.Я. Виленкина «За страницами учебника математики»
Искусны были египетские писцы и гарпедонапты! Но однажды им пришлось устыдиться, потому что пришелец из далекой Греции оказался намного искуснее их. Это случилось в VI веке до новой эры, а пришельцем был … Фалес из Милета. В те времена греки не занимались геометрией, и Фалес решил на месте познакомиться с египетской наукой. Египтяне дали ему трудную задачу: как найти высоту одной из громадных пирамид? Фалес нашел для этой задачи простое и красивое решение (а в математике очень часто простота – признак красоты). Он воткнул длинную палку вертикально в землю и сказал: «Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды».
Чтобы сообразить это, Фалес должен был уже много знать про геометрические фигуры, а особенно про ту, которая получается, если разбить квадрат на два треугольника. А дальше, вероятно, Фалес рассуждал так.
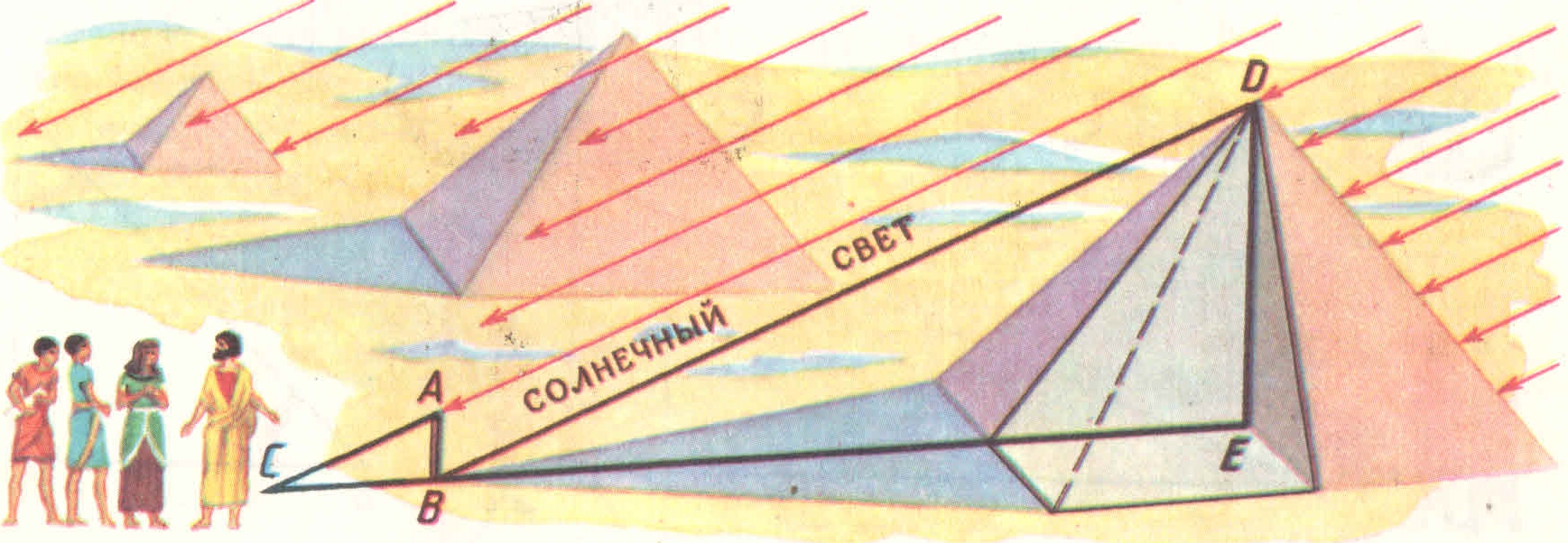
Солнце от Земли очень далеко, поэтому идущие от него и к пирамиде лучи можно без большой ошибки считать параллельными. Но когда тень от палки станет той же длины, что и сама палка, то треугольник АВС станет прямоугольным и равнобедренным. А из параллельности солнечных лучей он вывел, что тогда и треугольник DEC на том же рисунке тоже станет равнобедренным, а значит, высота пирамиды будет равна длине её тени.
Из книги Я.И. Перельмана «Занимательная геометрия»
Самый легкий и самый древний способ — без сомнения, тот, которым греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Жрецы и фараон, собравшиеся у подножия высочайшей пирамиды, озадаченно смотрели на северного пришельца, отгадывавшего по тени высоту огромного сооружения.
Фалес, — говорит предание, — избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна также равняться длине отбрасываемой ею тени ('). Вот, пожалуй, единственный случай, когда человек извлекает пользу из своей тени...
Задача греческого мудреца представляется нам теперь детски-простой, но не будем забывать, что смотрим мы на нее с высоты геометрического здания, воздвигнутого уже после Фалеса. Он жил задолго до Евклида, автора замечательной книги, по которой обучались геометрии в течение двух тысячелетий после его смерти. Заключенные в ней истины, известные теперь каждому школьнику, не были еще открыты в эпоху Фалеса. А чтобы воспользоваться тенью для решения задачи о высоте пирамиды, надо было знать уже некоторые геометрические свойства треугольника, — именно следующие два (из которых первое Фалес сам открыл):
1) что углы при основании равнобедренного треугольника равны, и обратно—что стороны, лежащие против равных углов треугольника, равны между собою;
2) что сумма углов всякого треугольника (или по крайней мере прямоугольного) равна двум прямым углам.
Только вооруженный этим знанием Фалес вправе был заключить, что, когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и, следовательно, вершина пирамиды, середина ее основания и конец ее тени должны обозначить равнобедренный треугольник. Этим простым способом очень удобно, казалось бы, пользоваться в ясный солнечный день для измерения одиноко стоящих деревьев, тень которых не сливается с тенью соседних.
Но в наших широтах не так легко, как в Египте, подстеречь нужный для этого момент: Солнце у нас низко стоит над горизонтом, и тени бывают равны высоте отбрасывающих их предметов лишь в околополуденные часы летних месяцев. Поэтому способ Фалеса в указанном виде применим не всегда.
Рис.1 Измерение высоты дерева по тени.
Нетрудно, однако, изменить этот способ так, чтобы в солнечный день можно было пользоваться любой тенью, какой бы длины она ни была. Измерив, кроме того, и свою тень или тень какого-нибудь шеста, вычисляют искомую высоту из пропорции (рис. 1):
AB:ab==BC:bc
т. е. высота дерева во столько же раз больше вашей собственной высоты (или высоты шеста), во сколько раз тень дерева длиннее вашей тени (или тени шеста). Это вытекает, конечно, из геометрического подобия треугольников ABC и аbc (по двум углам).
Иные читатели возразят, пожалуй, что столь элементарный прием не нуждается вовсе в геометрическом обосновании: неужели и без геометрии неясно, что во сколько раз дерево выше, во столько раз и тень его длиннее? Дело, однако, не так просто, как кажется. Попробуйте применить это правило
к теням, отбрасываемым при свете уличного фонаря или лампы,— оно не оправдается. На рис. 2 вы видите, что столбик АВ выше тумбы ab примерно втрое, а тень столбика больше тени тумбы (ВС:bс) раз в восемь. Объяснить, почему в данном случае способ применим, а в другом нет, — невозможно
без геометрии.
Рис.2 Когда такое измерение не выполнимо.
Рассмотрим поближе, в чем тут разница. Суть дела сводится к тому, что солнечные лучи между собою параллельны, лучи же фонаря — непараллельны. Последнее очевидно; но почему вправе мы считать лучи Солнца параллельными, хотя они безусловно пересекаются в том месте, откуда исходят?
Решение
Лучи Солнца, падающие на Землю, мы можем считать параллельными потому, что угол между ними чрезвычайно мал, практически неуловим. Несложный геометрический расчет убедит вас в этом. Вообразите два луча, исходящие из какой-нибудь точки Солнца и падающие на Землю в расстоянии, скажем, одного километра друг от друга. Значит, если бы мы поставили одну ножку циркуля в эту точку Солнца, а другою описали окружность радиусом, равным расстоянию от Солнца до Земли (т. е. радиусом в 150 000 000 км) то между нашими двумя лучами-радиусами оказалась бы дуга в один километр длиною. Полная длина этой исполинской окружности была бы равна 2π× 150 000 000км = 940 000 000 км. Один градус ее, конечно, в 360 раз меньше, т. е. около 2 600 000 км; одна дуговая минута в 60 раз меньше градуса, т. е. равна 43000 км, а одна дуговая секунда еще в 60 раз меньше,
т. е. 720 км. Но наша дуга имеет в длину всего только 1 км; значит, она соответствует углу в 
секунды. Такой ничтожный угол неуловим даже для точнейших астрономических инструментов; следовательно, на практике мы можем считать лучи Солнца, падающие на Землю, за параллельные прямые. Если бы эти геометрические соображения не были нам известны, мы не могли бы обосновать рассматриваемый способ определения высоты по тени. Пробуя применить способ теней на практике, вы сразу же убедитесь, однако, в его ненадёжности. Тени не отграничены так отчетливо, чтобы измерение их длины можно было выполнить вполне точно. Каждая тень, отбрасываемая при свете Солнца, имеет неясно очерченную серую кайму полутени, которая и придает границе тени неопределенность. Происходит это оттого, что Солнце — не точка, а большое светящееся тело, испускающее лучи из многих точек. На рис. 3 показано, почему вследствие этого тень ВС дерева имеет еще придаток в виде полутени CD, постепенно сходящей на-нет.
Рис. 3 Как образуется полутень.
Угол CAD между крайними границами полутени равен тому углу, под которыми мы всегда видим солнечный диск, т. е. половине градуса. Ошибка, происходящая от того, что обе тени измеряются не вполне точно, может при неслишком даже низком стоянии Солнца достигать 5% и более. Эта ошибка прибавляется к другим неизбежным ошибкам — от неровности почвы и т.д.—и делает окончательный результат мало надежным. В местности гористой, например, способ этот совершенно неприменим.
Еще два способа
Вполне возможно обойтись при измерении высоты и без помощи теней. Таких способов много; начнем с двух простейших. Прежде всего мы можем воспользоваться свойством равнобедренного прямоугольного треугольника, обратившись к услугам весьма простого прибора, который весьма легко изготовить из дощечки и трех булавок. На дощечке любой формы, даже на куске коры, если у него есть плоская сторона, намечают три точки — вершины равнобедренного прямоугольного треугольника— и в них втыкают торчком по булавке (рис. 4).
Рис.4 Булавочный прибор для измерения высот.
Пусть у вас нет под рукой чертежного треугольника для построения прямого угла, нет и циркуля для отложения равных сторон. Перегните тогда любой лоскут бумаги один раз, а затем поперек первого сгиба еще раз так, чтобы обе части первого сгиба совпали, — и получите прямой угол. Та же бумажка пригодится и вместо циркуля, чтобы отмерить равные расстояния.
Как видите, прибор может быть целиком изготовлен в бивуачной обстановке.
Обращение с ним не сложнее изготовления. Отойдя от измеряемого дерева, держите прибор так, чтобы один из катетов треугольника был направлен отвесно, для чего можете пользоваться ниточкой с грузиком, привязанной к верхней булавке.
Рис.5 Схема применения булавочного прибора.
Приближаясь к дереву или удаляясь от него, вы всегда найдете такое место А (рис. 5), из которого, глядя на булавки a и c, увидите, что они покрывают верхушку С дерева: это значит, что продолжение гипотенузы ас проходит через точку С. Тогда, очевидно, расстояние аВ равно СВ, так как угол α = 45°. Следовательно, измерив расстояние аВ (или, на ровном месте, одинаковое с ним расстояние AD) и прибавив BD, т. е. возвышение аА глаза над землей, получите искомую высоту дерева.
По другому способу вы обходитесь даже и без булавочного прибора. Здесь нужен шест, который вам придется воткнуть отвесно в землю так, чтобы выступающая часть как раз равнялась вашему росту. Место для шеста надо выбрать так, чтобы, лежа, как показано на рис. 6, вы видели верхушку дерева на одной прямой линии с верхней точкой шеста. Так как треугольник Abc— равнобедренный и прямоугольный, то угол А = 45° и, следовательно, АВ равно ВС, т. е. искомой высоте дерева.
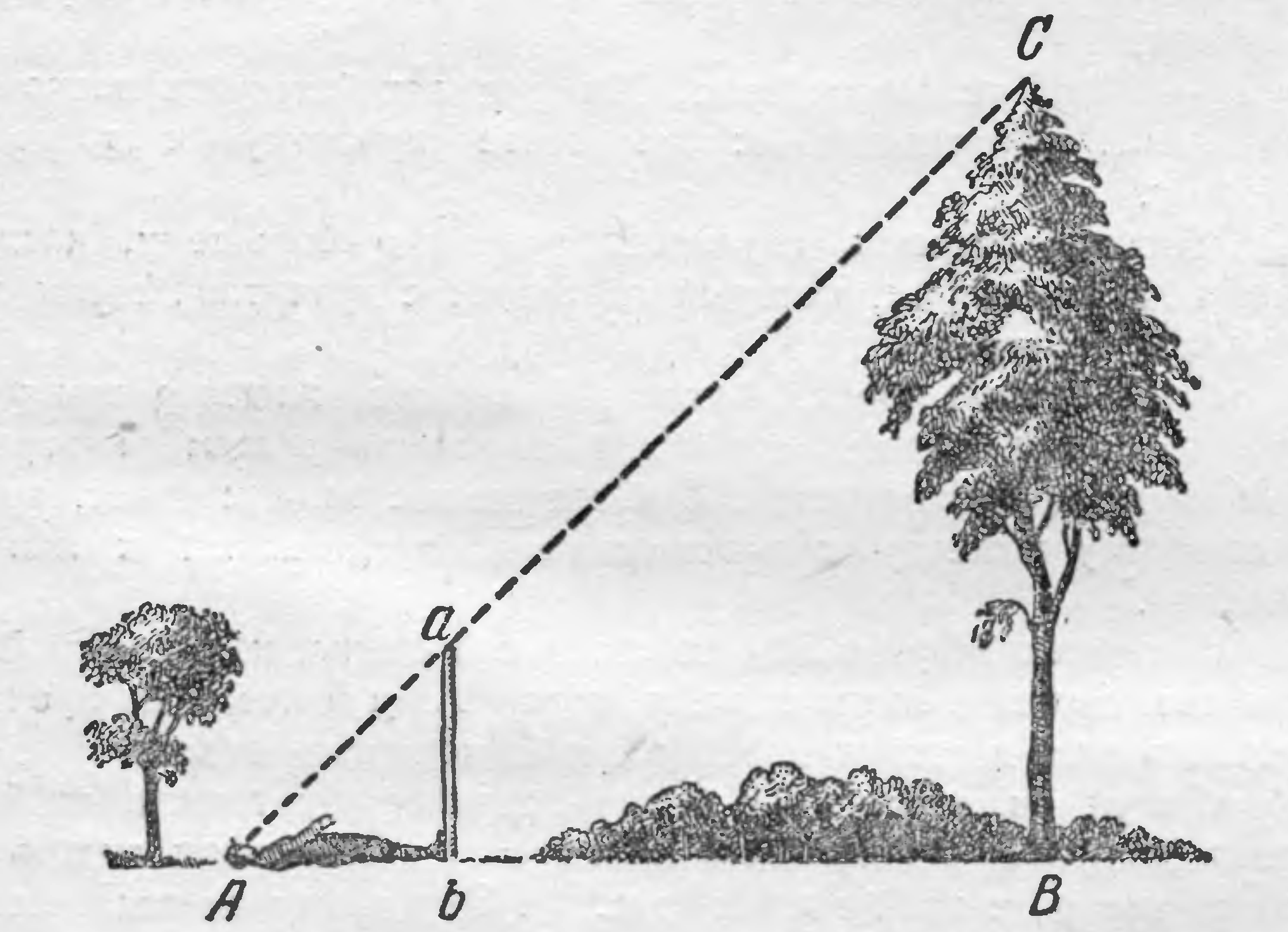
Рис.6 Ещё один способ измерения высоты дерева.
Как поступил сержант
Некоторые из только что описанных способов измерения высоты неудобны тем, что вызывают необходимость ложиться на землю. Можно, разумеется, избежать такого неудобства. Вот как однажды было на одном из фронтов Великой Отечественной войны. Подразделению лейтенанта Иванюк было приказано построить мост через горную реку. На противоположном берегу засели фашисты. Для разведки места постройки моста лейтенант выделил разведывательную группу во главе со старшим сержантом Поповым... В ближайшем лесном массиве они измерили диаметр и высоту наиболее типичных деревьев и подсчитали количество деревьев, 
Рис.8 Измерение высоты дерева при помощи шеста.
которые можно было использовать для постройки. Высоту деревьев определяли при помощи вешки (шеста) так, как показано на рис. 8.
Этот способ состоит в следующем. Запасшись шестом выше своего роста, воткните его в землю отвесно на некотором расстоянии от измеряемого дерева (рис. 8). Отойдите от шеста назад, по продолжению Dd до того места А, с которого, глядя на вершину дерева, вы увидите на одной линии с ней верхнюю точку b шеста. Затем, не меняя положения головы, смотрите по направлению горизонтальной прямой аС, замечая точки с и С, в которых луч зрения встречает шест и ствол. Попросите помощника сделать в этих местах пометки, и наблюдение окончено. Остается только на основании подобия треугольников abc и аВС вычислить ВС из пропорции ВС:bc=aC:ac
откуда ВС=Ьс· 
Расстояния bс, аС и ас легко измерить непосредственно. К полученной величине ВС нужно прибавить расстояние CD (которое также измеряется непосредственно), чтобы узнать искомую высоту дерева.
Для определения количества деревьев старший сержант приказал солдатам измерить площадь лесного массива. Затем он подсчитал количество деревьев на небольшом участке размером 50X50 кв. м и произвел соответствующее умножение.
На основании всех данных, собранных разведчиками, командир подразделения установил, где и какой мост нужно строить. Мост построили к сроку, боевое задание было выполнено успешно.