Интегрирование иррациональных выражений

Таблица интегралов

1.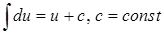
2.
3.
4.
5.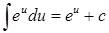
6.
7.
8.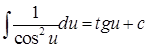
9.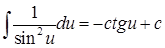
10.
11.
12.
13.
14.

 

 

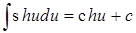
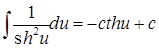
Таблица производных

1. Степенная функция:
2. Показательная функция:
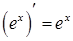
3. Логарифмическая функция:
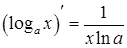
4. Тригонометрические функции:
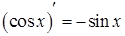
5. Обратные тригонометрические функции:
6. Гиперболические функции

 

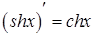
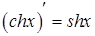
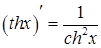
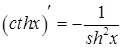
Свойства интегралов

1.

2.

3.

4.

5.

 

Правила интегрирования

1.

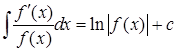
Если числитель подынтегральной дроби-производная знаменателя, то интеграл равен натуральному логарифму модуля знаменателя.

2.

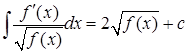
Если числитель подынтегральной дроби-производная подкоренного выражения квадратного корня, стоящего в знаменателе, то такой интеграл равен двум таким корням.

3. Если известно, ч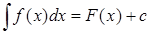то , то

1)

2)

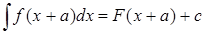
3)

Например: ,

. .

 

Интегрирование по частям:

Подынтегральное выражение	u	dv

 

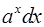
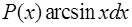
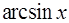
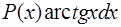
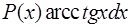
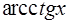
Тогда ,

Интегрирование простейших дробей

I.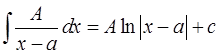

II.

III.

1) выделить в знаменателе полный квадрат;

2) ввести линейную подстановку;

3) поделить почленно

Интегрирование рациональных дробей.

 

1. Если дробь неправильная (степень числителя больше или равна степени знаменателя) выделить целую часть с помощью деления уголком. Если дробь правильная, то сразу перейти к пункту 2.

2. Разложить правильную рациональную дробь на простейшие дроби:

1) Разложить на простейшие множители знаменатель. Простейшие множители-линейные вида и квадратичные с дискриминантом меньше 0.

2) В зависимости от разложения знаменатель разложить дробь по правилу:

где A_i, B_i, M_i, N_i, R_i, S_i – некоторые постоянные величины.

При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин A_i, B_i, M_i, N_i, R_i, S_i применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.

3. Проинтегрировать сумму простейших дробей (см выше)

 

Интегрирование тригонометрических функций:

Универсальная тригонометрическая подстановка

,

2. Если функция нечетна относительно синуса, то подстановка ;

3. Если функция нечетна относительно косинуса синуса, то подстановка ;

4. Если функция четна относительно синуса косинуса, то подстановка

 

,

 

5.

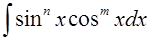
1) Если хотя бы одна из степеней нечетна, то:

-отделить от нечетной степени один множитель;

-оставшуюся четную степень выразить через кофункцию из основного тригонометрического тождества ;

-ввести подстановку: кофункцию обозначить за новую переменную.

 

2) Если обе степени четные. то следует применить формулы понижения степени:

3) Если сумма степеней четная отрицательная, то подстановка

Интегрирование иррациональных выражений

1. Если в состав иррациональной функции входят корни различных степеней из одного и того же выражения, то в это выражение следует обозначить за новую переменную в степени равной наименьшему общему кратному степеней корней, входящих в выражение.

2. 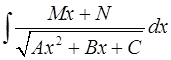: выделить под корнем полный квадрат, ввести линейную подстановку, почленно разделить при необходимости, в результате получатся табличные интегралы или сводящиеся к табличным.

3. ; 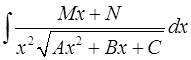: подстановкой интеграл сводят к виду 2.

4.

интеграл	подстановка

 

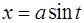
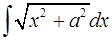
5. : выделением полного квадрата и введением линейной подстановки интеграл сводят к одному из интегралов п.4