4.1
Видимость ребер призмы на П2 верно изображена на чертеже: 1,2, 3, 4
1. 2. 3. 4.
4.2
Видимость ребер пирамиды на П1 верно изображена на чертеже: 1, 2, 3, 4
1. 2. 3. 4.
4.3
Даны чертежи поверхностей
1. 2. 3. 4. 5.
| Вопрос | Ответ |
| Многогранники изображены на чертеже … | 3,4 |
| Поверхность вращения изображена на чертеже … | 1,2,5 |
| Цилиндр изображен на чертеже … | |
| Конус изображен на чертеже … | |
| Призма изображена на чертеже … | |
| Пирамида изображена на чертеже … | |
| Сфера изображена на чертеже … |
4.4
Дан чертеж …
1. пирамиды трехгранной
2. плоскости
3. призмы трехгранной
4. цилиндра
5.призмы четырехгранной
4.5
Даны чертежи поверхностей:
1. 2. 3. 4.
5. 6. 7.
| Вопрос | Ответ |
| Пирамида изображена на чертеже … | |
| Призма изображена на чертеже … | |
| Многогранник изображен на чертеже … | 3,7 |
| Поверхность вращения изображена на чертеже … | |
| Конус изображен на чертеже … | |
| Линейчатая поверхность изображена на чертеже… | 2,3,5,7 |
| Цилиндрическая поверхность изображена на чертеже … | |
| Плоскость частного положения изображена на чертеже … | |
| Плоскость общего положения изображена на чертеже … |
4.6
Даны композиции из геометрических фигур:
пирамиды и цилиндра - 4
конуса и призмы- 1
цилиндра и призмы - 2
двух призм - 3
1 2 3 4
4. 7
Грань SAB данной пирамиды - 1
Грань ABС данной пирамиды - 4
Грань SAС данной пирамиды - 3
1. перпендикулярна профильной плоскости проекций
2. принадлежит фронтальной плоскости проекций
3. является плоскостью общего положения
4. параллельна горизонтальной плоскости проекций
ПОЗИЦИОННЫЕ ЗАДАЧИ
Параллельность на чертеже
5.1
Параллельные прямые a и b изображены на чертеже: 1, 2, 3, 4
1. 2. 3. 4.
5.2
Плоскости Σ (m ║ n) параллельна плоскость:1, 2, 3, 4
1. ∆(b ∩ l)
2. ∆(a ∩ c)
3. ∆(a ∩ b)
4. ∆(c ∩ b)
5. 3
Плоскость Σ(d ∩e) параллельна:
плоскости G(ABC) на чертеже 1
плоскости Q(a∩b) на чертеже 2
плоскости R(ABC ) на чертеже 3
плоскости ∆( a║b) на чертеже 4
.
5.4
Прямая m параллельна плоскости Σ(АВС) на чертеже: 1, 2, 3
1. 2. 3.
5.5
Прямая m параллельна прямой в плоскости Σ(АВС) на чертеже: 1, 2, 3, 4
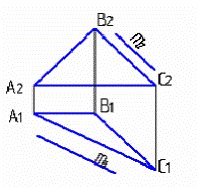
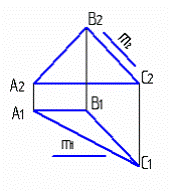
1 2 3 4
5.7
Прямая m не параллельна плоскости Q(АВС) на чертеже: 1, 2, 3, 4
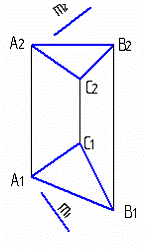
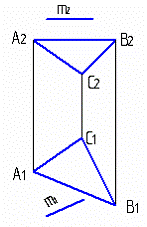
1. 2. 3. 4.
Принадлежность точки и линии плоскости и поверхности
6.1
Прямой n принадлежит точка: A, B, C, D
6.2
Плоскости Σ(m║ n) принадлежит точка:
A, B, C, D
6.3
Прямой t принадлежит точка …
1. G
2. А
3. D
4. E
5. С
6. В
6.4
На комплексном чертеже прямая принадлежит плоскости, если проекции … принадлежат соответствующим проекциям прямых, принадлежащих этой плоскости
1. трех её точек
2. одной её точки
3. четырех её точек
4. двух её точек
6.5
Поверхности пирамиды принадлежит точка:
A, B, C, E
6.6
Поверхности пирамиды не принадлежат точки:
A, B, C, E
6.7
Видимыми на фронтальной проекции
цилиндра являются точки…
1. С и А
2. В и Е
3. А и В
4. В и С
6.8
Точка А принадлежит поверхности конуса на чертеже: 1, 2, 3, 4
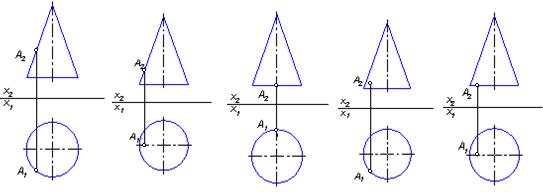
1. 2. 3. 4. 5.
6.9
На поверхности сферы дана линия.
Горизонтальная проекция этой сферы дана
на чертеже: 1, 2, 3, 4, 5
1. 2. 3. 4. 5.
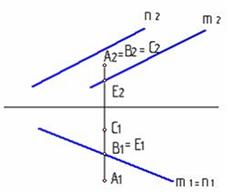6.10 Плоскости Σ(m║n) принадлежат точки:
1. А и С
2. А и В
3. В и Е
4. А и Е
 | |
 |
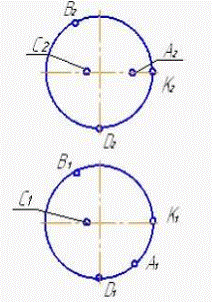
6.11
Поверхности сферы принадлежат точки:
1. А и К
2. С и В
3. К и С
4. В и D
Пересечение прямой с плоскостью, поверхностью, пересечение двух плоскостей
7.1
Прямую общего положения можно заключить в плоскость…
1. уровня
2. общего положения
3. проецирующую
7.2
Горизонтальную прямую можно заключить в плоскость частного положения -…
1. горизонтальную плоскость уровня
2. горизонтально-проецирующую плоскость
4. фронтально-проецирующую плоскость
5. фронтальную плоскость уровня
7.3
Точка пересечения К прямой m с плоскостью, заданной треугольником, правильно определена на чертеже: 1, 2, 3, 4
1. 2. 3. 4.
7.4
Точка пересечения K прямой l с плоскостью Σ(m∩n) правильно определена на чертеже: 1, 2, 3, 4
1. 2. 3. 4.
7.5
Для определения точки пересечения К прямой l и
плоскости общего положения Σ необходимо...
1. использовать способ сфер
2. определить ее как точку пересечения проекций заданной
прямой с проекцией одной из линий, задающих плоскость
3. использовать одну вспомогательную плоскость
4. использовать две вспомогательные плоскости
7.6
Прямая m пересекается с поверхностью сферы в точках:
1. А и D
2. F и D
3. B и C
4. E и P
5. F и K
7.7
Для решения задач на пересечение прямой общего положения и плоскости общего положения применяется вспомогательная …
1. плоскость общего положения
2. прямая частного положения
3. плоскость уровня
4. проецирующая плоскость
7.8
Для решения задач на пересечение плоскостей общего положения применяется:
1. одна плоскость общего положения
2. одна плоскость частного положения
3. две плоскости частного положения – плоскости уровня
4. проецирующая плоскость
7.9
Две горизонтально-проецирующие плоскости ∆ и ∆ ¢ пересе-
каются …
1. по прямой общего положения
2. по горизонтальной прямой
3. по горизонтально-проецирующей прямой
4. по фронтально-проецирующей прямой
7.10
Горизонтально-проецирующая плоскость∆ и
фронтально-проецирующая плоскость Q пересекаются…
1. по прямой общего положения
2. по горизонтальной прямой
3. по горизонтально-проецирующей прямой
4. по фронтально-проецирующей прямой
7.11
Линия пересечения плоскости, заданной треугольником, и плоскости Σ(m ║ n), правильно определена на чертеже: 1, 2, 3, 4
7.12
Горизонтальная Г и фронтальная Ф плоскости уровня пересекаются…
1. по прямой общего положения
2. по горизонтальной прямой
3. по горизонтально-проецирующей прямой
4. по фронтально-проецирующей прямой
5. по профильно-проецирующей прямой