Матричная форма
Система линейных уравнений может быть представлена в матричной форме как:

или, согласно правилу перемножения матриц,
AX = B.
Если к матрице А прибавить столбец свободных членов, то А называется расширенной матрицей.
Метод Крамера
Применяется для решения квадратных систем уравнений и определитель должен быть не равен нулю.
Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di/D, где D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Билет 11. Метод Гаусса решения произвольных систем линейных алгебраических уравнений. Привести пример.
Метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных находятся все остальные переменные.
Пример
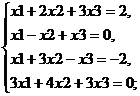
Выписываем расширенную матрицу
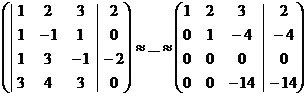
x1 + 2x2 + 3x3 = 2
x2 – 4x3 = -4
-14x3 = -14
x3=1, x2=0, x1=-1
Билет 12. Решение системы линейных алгебраических уравнений матричным методом (с помощью обратной матрицы). Привести пример.
Матричный метод.
Систему можно переписать в матричной форме:
AX = B, где A — основная матрица системы, B и X — столбцы свободных
членов и решений системы соответственно:
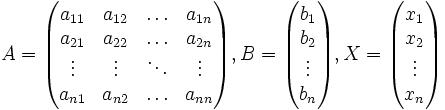
множим это матричное уравнение слева на A - 1 — матрицу, обратную к матрице A: 
Так как A −1A = E, получаем X = A -1B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (число Ур-й равно числу неизвестных)является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

Пример:

Сначала убедимся в том, что определитель матрицы не равен нулю

Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.


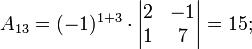

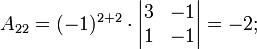




Далее найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы

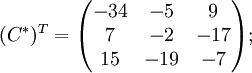
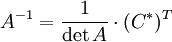
Подставляя переменные в формулу, получаем:

Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов
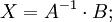
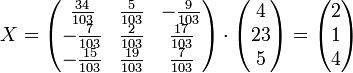
Итак, x=2; y=1; z=4
Билет 13. Исследование систем линейных алгебраических уравнений с помощью теоремы Кронекера-Капелли.
Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
Доказательство
Необходимость
Пусть система совместна. Тогда существуют числа  такие, что
такие, что  . Следовательно, столбец b является линейной комбинацией столбцов
. Следовательно, столбец b является линейной комбинацией столбцов  матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что
матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что 
Достаточность
Пусть 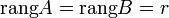 . Возьмем в матрице A какой-нибудь базисный минор. Так как
. Возьмем в матрице A какой-нибудь базисный минор. Так как 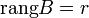 то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.
то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.
Следствия
1.Количество главных переменных системы равно рангу системы.
2.Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
Билет 14. Системы линейных однородных уравнений. Свойства их решений.
Однородные СЛУ имеют вид
а11х1+а12х2+…+a1nxn=0
a21x1+a22x2+…+a2nxn=0
……………………………
am1x1+am2x2+…+amnxn=0
Однородные СЛУ всегда совместны, то есть имеет хотя бы одно решение.
Свойства:
х1=к1, х2=к2,…,хn=kn
е1=(k1,k2,…,kn)
1.если строка е1=(k1,k2,…,kn) – решение системы, то и строка ʎе1=(ʎk1, ʎk2,…, ʎkn) – тоже будет являться решением системы.
2.если строки е1=(k1,k2,…,kn) и е2=(l1,l2,ln) – решения систмы, то при любых с1 и с2 их линейный комбинации с1е1+с2е2=(c1k1+c2l1, c1k2+c2l2,…,c1kn+c2ln) – тоже решение системы.
Билет 15. Структура общего решения системы линейных однородных алгебраических уравнений.
Общее решение однородных СЛУ. Структура общего решения однородных СЛУ.
Общее решение однородных СЛУ имеет вид:
c1e1+c2e2+…+ckek, где е1,e2,…,ek – фундаментальная система решений, а c1,c2,...,ck – произвольные числа и k=n-r.
Общее решение системы m линейных уравнений с n переменными равно сумме общего решения соответсвующей системе однородных СЛУ и произвольного частного решения этой системы.
Билет 16. Общее решение систем линейных алгебраических уравнений.
????????
Билет 17. Понятие линейного пространства. Примеры
Рассмотрим такое множество R элементов x, y, z…, в котором для любых 2 элементов xЄR и yЄR определена сумма x+yЄR и для любого элемента xЄR и любого действительного числа λ определено произведение λxЄR.
Если сложение элементов множества R и умножение действительного числа λ на элемент удовлетворяет условиям:
1) x+y = y+x
2) (x+y)+z = x+(y+z)
3) существует такой элемент ОЄR (нуль-элемент), что x+0 = x для любого xЄR
4) для каждого xЄR существует yЄR такой, что x+y = 0 (y = -x)
5) 1*x = x
6) λ(µx) = (λµ)x
7) (λ+µ)x = λx + µx
8) λ(x+y) = λx + λy
то множество R – линейное (или векторное), а элементы x, y, z… этого пространства называются векторами.
1. В каждом линейном пространстве существует только один нуль-элемент.
2. Для каждого элемента линейного пространства существует только 1 противоположный элемент.
3. Для каждого xЄR выполняется 0x = 0
4. Для любого действительного λ и ОЄR x, λ = 0
5. Из равенства λx = 0 следует x = 0 или λ = 0
6. элемент (-1)*x противоположный элементу x
Билет 18. Линейная зависимость и независимость системы векторов линейного пространства. Базис линейного пространства. Пример.
Если в линейном пространстве R имеется n линейно независимых векторов, но любые n +1 векторов этого пространства линейно зависимы, то пространство R называют n -мерным. Принято также говорить, что размерность пространства R равна n и писать d(R)= n. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным и d(R) = ∞.
Совокупность n линейно независимых векторов n -мерного линейного пространства называется базисом.
Пусть x, y, z, …, u – какие-нибудь векторы линейного пространства R. Вектор, определяемый равенством
v = αx + βy + γz + … + λu,
где α, β, γ, …, λ – действительные числа, также принадлежат линейному пространству R. Этот вектор называется линейной комбинацией векторов x, y, z, …, u.
Пусть линейная комбинация векторов x, y, z, …, u является нуль-вектором, т.е.
αx + βy + γz + … + λu, = 0
Векторы x, y, z, …, u называются линейно независимыми, если равенство выполняется лишь при α = β = γ = … = λ=0. Если же равенство может выполняется только в том случае, когда не все числа α, β, γ, …, λ равны нулю, то говорят, что векторы x, y, z, …, u линейно зависимы. Векторы x, y, z, …, u линейно зависимы тогда и только тогда, когда один из этих векторов может быть представлен в виде линейной комбинации остальных векторов.
Билет 19. Координаты векторов линейного пространства. Единственность разложения вектора по заданному базису.
Если в линейном пространстве R имеется n линейно независимых векторов, но любые n +1 векторов этого пространства линейно зависимы, то пространство R называют n -мерным. Принято также говорить, что размерность пространства R равна n и писать d(R)= n. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным и d(R) = ∞.
Совокупность n линейно независимых векторов n -мерного линейного пространства называется базисом. Справедлива следующая теорема: каждый вектор линейного n-мерного пространства может быть единственным образом представлен в виде линейной комбинации векторов базиса. Так, если e1, e2, …., en – базис n -мерного линейного пространства R, то любой вектор xЄR может быть единственным образом представлен в виде:
x = ξ1e1 + ξ2e2 + … + ξnen.
Таким образом, вектор x в базисе e1, e2, …., en определяется единственным образом с помощью чисел ξ1, ξ2, …, ξn. Эти числа называются координатами вектора x в данном базисе.
Если x = ξ1e1 + ξ2e2 + … + ξnen, y = η1e1 + η2e2 + … + ηnen, то x + y = (ξ1 + η1) e1 + (ξ2 + η2) e2 + … + (ξn + ηn) en, λx = λξ1e1 + λξ2e2 + … + λξnen.
Теорема. Каждый вектор x линейного пространства R можно представить и притом единственным образом в в идее линейной комбинации векторов базиса.
Пусть векторы e1, e2, …, en образуют базис произвольного n -мерного пространства R, векторы e1, e2, …, en и некоторый вектор x зависимы, тогда существуют такие не равные одновременно нулю числа λ1, λ2, …,λn, λ, что
λ1e1 + λ2e2 + …,λnen + λx = 0.
Причем λ≠0, потому что в противном случае векторы e1, e2, …, en были бы линейно зависимы. Следовательно,
x = x1e1 + x2e2 + … + xnen,
где xi = - λi/ λ(i = 1, 2, …, n), и это выражение вектора через базис единственное, так как если представить, например:
x = y1e1 + y2e2 + … + ynen,
то вычитая из него почленно первое получим:
(y1 – x1)e1 + (y2 – x2)e2 + … + (yn – xn)en = 0, т.е. y1 – x1 = 0 или y1 = x1.
Билет 20. Критерий линейной зависимости системы векторов. Ранг системы векторов. Привести примеры.
Пусть x, y, z, …, u – какие-нибудь векторы линейного пространства R. Вектор, определяемый равенством
v = αx + βy + γz + … + λu,
где α, β, γ, …, λ – действительные числа, также принадлежат линейному пространству R. Этот вектор называется линейной комбинацией векторов x, y, z, …, u.
Пусть линейная комбинация векторов x, y, z, …, u является нуль-вектором, т.е.
αx + βy + γz + … + λu, = 0
Векторы x, y, z, …, u называются линейно независимыми, если равенство выполняется лишь при α = β = γ = … = λ=0. Если же равенство может выполнятся только в том случае, когда не все числа α, β, γ, …, λ равны нулю, то говорят, что векторы x, y, z, …, u линейно зависимы. Векторы x, y, z, …, u линейно зависимы тогда и только тогда, когда один изз этих векторов может быть представлен в виде линейной комбинации остальных векторов.
Число векторов в базисе системы называется рангом системы векторов. Определение ранга корректно, а именно, если есть два различных базиса a1, a2, …, ak и b1, b2, …, bm некоторой системы векторов, то число базисных векторов в обоих базисах одинаково. Согласно определению базиса любой вектор из a1, a2, …, akможет быть выражен как линейная комбинация b1, b2, …, bm. Так, если k > m, то a1, a2, …, akявляются линейно зависимыми, но это невозможно, потому что эти векторы являются базисом системы. Аналогично можно доказывать, что случай m > k невозможен. Таким образом, m = k. Из этой теоремы следует, что если мы используем некоторые обратимые линейные преобразования векторов, ранг системы остается неизменным. Например, можно использовать преобразование Гаусса, чтобы упростить систему.
Билет 21. Преобразование координат вектора при переходе к новому базису.
Пусть в линейном n -мерном пространстве R имеются два базиса старый e1, e2, …, en и новый e’1, e’2, …, e’n. Даны зависимости, выражающие каждый вектор нового базиса через векторы старого:
e’1 = a11e1 + a21e2 + … + an1en
e’2 = a12e1 + a22e2 + … + an2en
........................................................
e’n = a1ne1 + a2ne2 + … + annen
Матрицу  называют матрицей перехода от старого базиса к новому.
называют матрицей перехода от старого базиса к новому.
Возьмем какой-нибудь вектор x, пусть (α1, α2, …, αn) его координаты старом базисе, а (α’1, α’2, …, α’n) – в новом. Старые координаты выражаются через новые по формулам:
α1 = a11α’1, + a12α’2 + … +a1nα’n
α2 = a21α’1, + a22α’2 + … +a2nα’n
…………………………………………………………
αn = an1α’1, + an2α’2 + … +annα’n
Это формулы преобразования координат.
Столбцы матрицы А это координаты в формулах перехода от старого базиса к новому, а строки – координаты в формулах преобразования старых координат через новые.
Билет 22.Евклидово пространство. Длина вектора и угол между его векторами
Линейное пространство R называется евклидовым, если имеется правило, которое позволяет для каждых 2 векторов x и y из R построить действительное число, называемое скалярным произведением x и y и обозначаемое (x,y), это праивло удовлетворяет следующим условиям:
1. (x,y) = (y,x)
2. (x, y+z) = (x,y) + (x,z)
3. (λx, y) = λ(x,y)
4. (x,x)>0, если x≠0
Из этих условий следует:
а)(y+z, x) = (y,x)+(z,x)
б)(x, λy) = λ(x,y)
в)(0,x) = 0 для любого x
Скалярное произведение любого вектора xЄR на себя называется скалярным квадратом вектора x.
Длина вектора x в евклидовом пространстве – квадратный корень из скалярного квадрата этого вектора | x | = √(x,x).
Угол φ, определяемый равенством  и принадлежит отрезку [0;π], называется углом между векторами x и y ортогональны и пишут x┴y.
и принадлежит отрезку [0;π], называется углом между векторами x и y ортогональны и пишут x┴y.
Билет 23. Ортогональные векторы. Ортонормированный базис евклидова пространства. Длина вектора и угол между векторами в ортонормированном базисе.
Базис e1, e2, …, en евклидова пространства называется ортогональным, если (ei, ek) = 0, при i≠k.
Справедлива следующая теорема: во всяком евклидовом пространстве имеется ортогональный базис. Если ортогональный базис состоит из нормированных векторов, то этот базис называется ортонормированным. Для ортогонального базиса e1, e2, …, en выполняются равенства
(ei, ek)= 
Если в n -мерном евклидовом пространстве известен какой-нибудь базис f1, f2, …, fn