Практическая работа № 12
Цель: познакомится с инструментом поиск решения, научится применять поиск решения для решения задач в MS Excel 2007.
Ход работы:
& Команды Поиск решения в стандартной установке программы, может не быть, установим её:
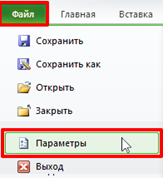
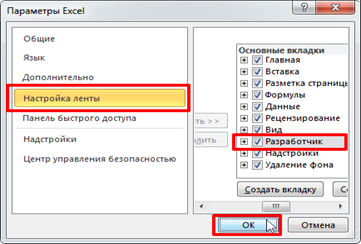
1. Проверяем есть ли в ленте программы, вкладка Разработчик: Файл/Параметры, затем Настройка ленты ставим галку над переключателем Разработчик:
| 
|
2. Установим надстройку Поиск решения: вкладка Разработчик группа Надстройки, кнопка также называется Надстройки, в окне Надстройки активируем переключатель Поиск решения нажимаем ОК
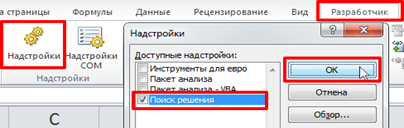
Теперь можем вызвать команду Поиск решения, вкладка Данные группа Анализ, кнопка Поиск решения:

&
: Упражнение 1. Предположим, что Вы начальник производственного отдела и Вам предстоит распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами, Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.
Первым делом создаём таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат - это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).
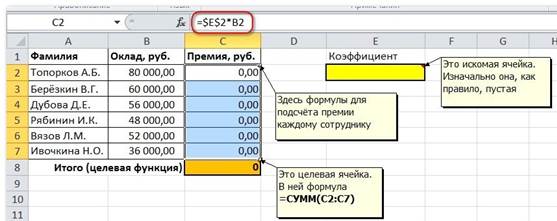
Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:
Начиная с Excel 2010
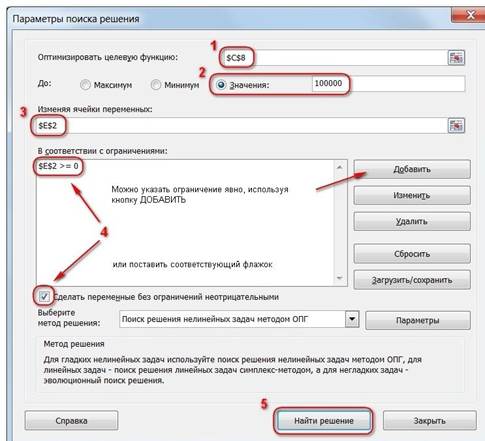
До Excel 2010
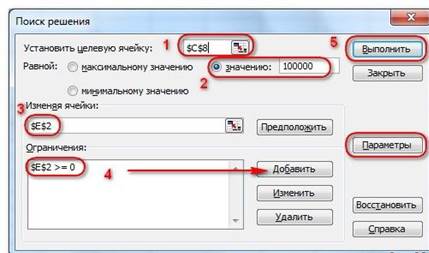
- Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна
- Варианты оптимизации: максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода
- Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение
4. Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимо всем понятных знаков =, >=, <=, при задании ограничений можно использовать варианты цел (целое), бин (бинарное или двоичное, т.е. 0 или 1), раз (все разные - только начиная с версии Excel 2010).
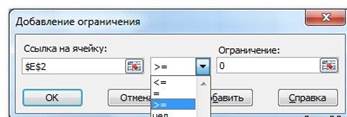
В данном примере ограничение только одно: коэффициент должен быть положительным. Это ограничение можно задать по-разному: либо установить явно, воспользовавшись кнопкой Добавить, либо поставить флажок Сделать переменные без ограничений неотрицательными.
Для версий до Excel 2010 этот флажок можно найти в диалоговом окне Параметры Поиска решения, которое открывается при нажатии на кнопку Параметры
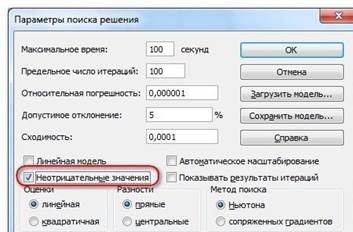
- Кнопка, включающая итеративные вычисления с заданными параметрами.
После нажатия кнопки Найти решение (Выполнить) Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.
Начиная с Excel 2010
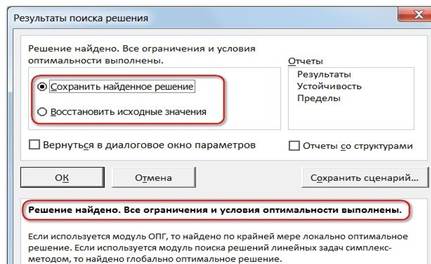
До Excel 2010

Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОК и фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена и возвращаетесь к предыдущему состоянию таблицы.
Решение данной задачи выглядит так
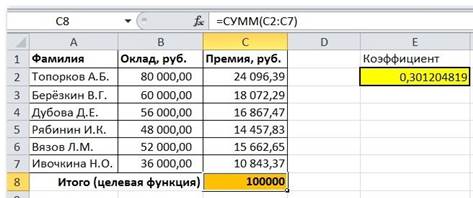
Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.
: Упражнение 2. Мебельное производство (максимизация прибыли)
Фирма производит две модели А и В сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.
Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В - 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю. Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В - 30 мин. в неделю можно использовать 160 ч машинного времени. Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В - 120 руб. прибыли?
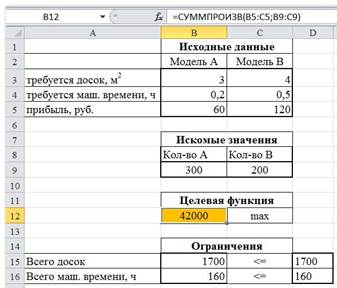
Сначала создаем таблицы с исходными данными и формулами:
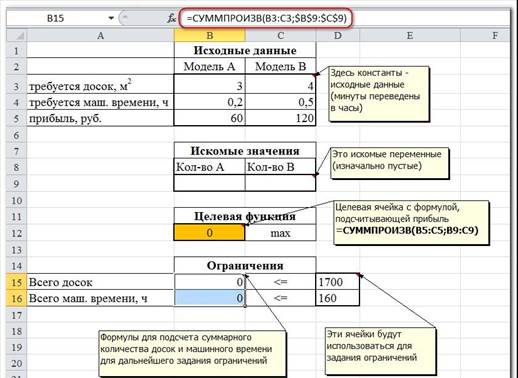
В ячейку В12 введите формулу =СУММПРОИЗВ(B5:C5;B9:C9) в ячейку В15 введите формулу =СУММПРОИЗВ(B3:C3;$B$9:$C$9), в ячейку В16 =СУММПРОИЗВ(B4:C4;$B$9:$C$9). Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры:
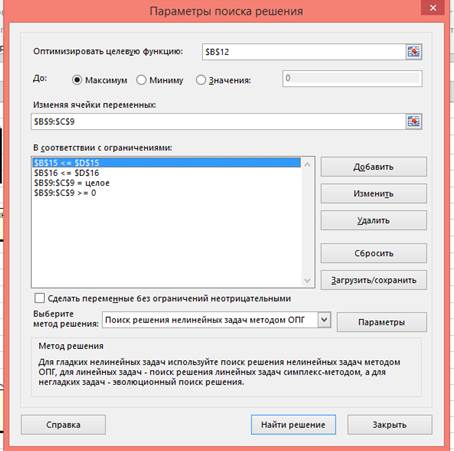
1. Целевая ячейка В12 содержит формулу для расчёта прибыли
2. Параметр оптимизации - максимум
3. Изменяемые ячейки В9:С9
4. Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице
5. Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат
: Упражнение 3. Транспортная задача (минимизация затрат)
В хозяйстве имеются пять складов минеральных удобрений и четыре пункта, куда их необходимо доставить. Потребность каждого пункта в минеральных удобрениях различна, и запасы на каждом складе ограничены. Требуется определить, с какого склада, в какой пункт поставлять, сколько минеральных удобрений для минимизации грузооборота перевозок.
Имеются следующие исходные данные.
Наличие минеральных удобрений на складах.
| Склады | Наличие удобрений, т. |
| Склад №1 | |
| Склад №2 | |
| Склад №3 | |
| Склад №4 | |
| Склад №5 |
Потребность в минеральных удобрениях на различных пунктах.
| Пункты | Потребность в удобрениях, т. |
| 1 пункт | |
| 2 пункт | |
| 3 пункт | |
| 4 пункт |
Расстояния между складами и пунктами доставки.
| Пункт 1 | Пункт 2 | Пункт 3 | Пункт 4 | |
| Склад №1 | ||||
| Склад №2 | ||||
| Склад №3 | ||||
| Склад №4 | ||||
| Склад №5 |
На пересечении столбца конкретного пункта доставки со строкой склада находится информация о расстояниях между этими пунктом доставки и складом. Например, расстояние между 3 пунктом и складом №3 равно 10 километрам.
Для решения задачи подготовим необходимые таблицы:
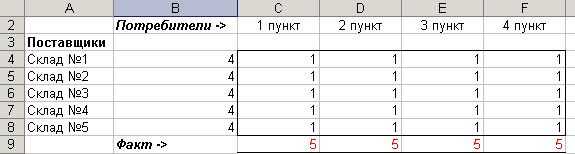
Значения ячеек по столбцу В с четвертой по восьмую строку определяются суммированием данных ячеек соответствующих строк начиная со столбца С до столбца F.
Например, значение ячейки B4=СУММ(C4:F4)
Значения ячеек по 9 строке по столбцам от С до F определяются суммированием данных ячеек соответствующих столбцов с 4 по 8 строки.
Например, значение ячейки С9=СУММ(C4:C8)
Каждое значение в ячейках на пересечении столбца конкретного пункта доставки и строки склада означает количество тонн, поставляемых с этого склада в данный пункт потребления. В нижней строке (строка 9) суммируется общее количество минеральных удобрений, поставляемых в определенный пункт доставки, а во втором столбце (столбец В) суммируется количество доставленного с конкретного склада минеральных удобрений.
Теперь, используя исходные данные, введем на этом же листе требуемые объемы поставок и расстояния между складами и пунктами доставки.
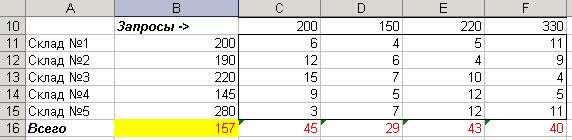
В строке 16 по столбцам C-F определим грузооборот по каждому пункту доставки. К примеру, для 1 пункта (ячейка С16) это рассчитывается с помощью формулы
С16=С4*С11+С5*С12+С6*С13+С7*С14+С8*С15
либо можно использовать функцию СУММПРОИЗВ
С16=СУММПРОИЗВ(C4:C8;C11:C15)
В ячейке С4 находится количество минеральных удобрений, перевозимых со склада №1 в 1 пункт доставки, а в ячейке С11 - расстояние от склада №1 до 1 пункта доставки. Соответственно первое слагаемое в формуле означает полный грузооборот по данному маршруту. Вся же формула вычисляет полный грузооборот перевозок минеральных удобрений в 1 пункт доставки.
В ячейке В16 по формуле = СУММ(С16:F16) будет вычисляться общий объем грузооборота минеральных удобрений.
Установите курсор ячейки в ячейку В16, выберите Данные – Поиск решения. После выбора данной команды появится одноименное диалоговое окно.
Поскольку в качестве критерия оптимизации нами выбрана минимизация грузооборота, в поле Установить целевую ячейку введите ссылку на ячейку, содержащую формулу расчета общего объема грузооборота минеральных удобрений. В нашем случае это ячейка $B$16. Чтобы минимизировать значение конечной ячейки путем изменения значений влияющих ячеек, переключатель установите в положение минимальному значению;
В поле Изменяя ячейки введите ссылки на изменяемые ячейки, разделяя их запятыми; либо, если ячейки находятся рядом, указывая первую и последнюю ячейку, разделяя их двоеточием ($С$4:$F$8). Это означает, что для достижения минимального грузооборота перевозок будут меняться значения в ячейках с С4 по F8, то есть будут изменяться количество груза, перевезенного по конкретному маршруту.
Если сейчас запустить процесс подбора параметров, то будет найден вариант, где все переменные равны нулю. И это правильно - если не перевозить ничего, то это самый дешевый вариант. Но нам необходимо перевезти минеральные удобрения, поэтому надо наложить некоторые ограничения для поиска решения.
Теперь добавим ограничения, которые следует наложить на значения в некоторых ячейках для правильного решения задачи.
Первое условие $B$4:$B$8 <=$B$11:$B$12. Оно означает, что значение в ячейке В4 должно быть меньше или равно значению в В11, в В5 меньше или равно, чем в В12, и так далее до В8 и В15.
В ячейках с В4 по В8 на листе находятся объемы поставок с конкретных складов. В ячейках с В11 по В15 - запасы на этих же складах. Так как невозможно вывести со склада больше, чем на нем есть, первое значение должно быть не больше второго.
Второе условие $С$4:$F$8>=0. Оно означает, что объем перевозок не может быть отрицательным, то есть, если на складе не хватает минеральных удобрений, их не везут с пункта доставки, на который эти минеральные удобрения были завезены ранее. Грузопоток имеет только одно направление - от складов к пунктам доставки удобрений.
И наконец, третье, и последнее условие $С$9:$F$9>=$C$10:$F$10. Оно означает, что значения в ячейках девятой строки должны быть больше или равны значениям в ячейках десятой строки, то есть запросы пунктов доставки минеральных удобрений должны быть выполнены полностью. Перевыполнение объема поставок допустимо, а недовыполнение - нет.
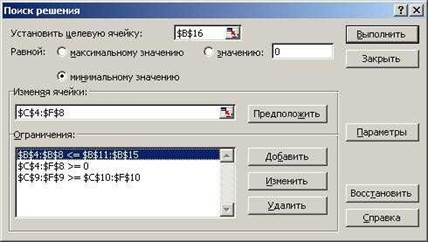
Введенные условия должны позволить найти наиболее оптимальный вариант решения задачи. Нажмите кнопку Выполнить для подбора решения.
После нахождения решения появляется диалог Результаты поиска решения. Нажав кнопку ОК, вы занесете вариант решения на рабочий лист.
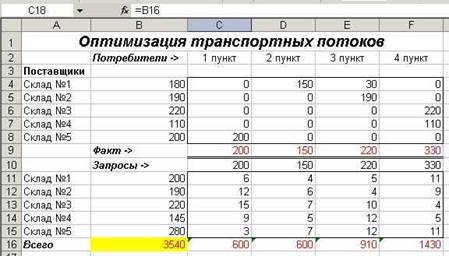
Минимальный грузооборот перевозок при соблюдении всех условий равен 3540 т.-км.
? Контрольные вопросы:
1. Для решения каких задач используют инструмент «Поиск решения»?
2. Как добавить команду «Поиск решения»?
3. Как вызвать команду «Поиск решения»?