Частотные характеристики двухполюсников.

 

Входное сопротивление и входная проводимость двухполюсника в общем случае являются функциями частоты ω. Под частотными характеристиками (ЧХ) понимают следующие типы характеристик:

1) зависимость модуля входного сопротивления (проводимости) от частоты ω.

2)зависимость действительной или мнимой части входного сопротив-ления (проводимости) от частоты ω.

ЧХ могут быть получены расчетным путем (если известны схема, ха-рактер элементов и их числовые значения) либо опытным (в этом случае схему двухполюсника и характер составляющих ее элементов можно и не знать). В общем случае двухполюсники содержат резистивные и реактивные элементы.

При снятии ЧХ опытным путем на вход двухполюсника подают на-пряжение, частоту которого изменяют в широких пределах, начиная с нуля, и по результатам измерений подсчитывают модуль входного сопротивления (проводимости) или действительную (мнимую) часть входного сопротивления (проводимости).

Реактивными двухполюсниками называют двухполюсники, состоящие только из реактивных элементов. Применительно к ним под ЧХ понимают зависимости X = f (ω) или b = f (ω).

ЧХ для несложных двухполюсников, содержащих резистивные и реактивные элементы, иногда можно качественно строить на основа­нии простых физических соображений о характере изменения сопротив­ления отдельных элементов этого двухполюсника в функции частоты. Если это сделать затруднительно, то прибегают к аналитическому расчету либо к снятию ЧХ опытным путем.

Качественно построим характеристику z = f (ω) для двухполюсника на рис. 3.17, а (рис. 3.17, б).

При ω = 0 (конденсатор представляет собой разрыв) z = R+R₁.

При ω → ∞, z = R+R_2, т.к.X_c =1/ ωC → ∞, а X_c =ωL → ∞.

При ω = ω’₀, имеет место режим резонанса токов и потому входное сопротивление имеет максимум. В области частот 0 - ω’₀ z имеет индуктивный характер, в области ω 0 - ∞ - емкостный.

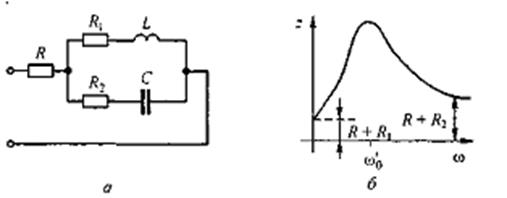
Рис.3.17

Если 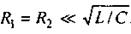, то при

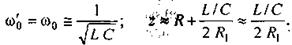
Рассмотрим вопрос о построении частотных характеристик реактивных двухполюсников, не содержащих резистивных сопротивлений. Входное сопротивление их Z = j X, а входная проводимость

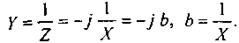
Частотная характеристика таких двухполюсников это зависимость Х(ω) или b (ω). Эти зависимости взаимно обратны.

Для индуктивного элемента Х(ω) = ω L (рис. 3.18, а), а b(ω) = 1/ ω L

(рис. 3.18, б). Для емкостного элемента b(ω) = - ω С (рис. 3.18 в), а Х(ω)=-1/ ω С (рис. 3.18, г).

Если учесть, что при последовательном соединении элементов сопротивления элементов складывают, то ясно, что для получения Х(ω) последовательно соединенных элементов надо сложить ординаты кривых Х(ω) этих элементов.

ЧХ последовательно соединенных L₁ и C₁ (рис. 3.18, д) построена на рис. 3.18, е в виде кривой 3 (прямая 1 - это ЧХ L₁, а кривая 2 - ЧХ C₁,). Зависимость b(ω) для схемы рис. 3.18, д изображена на рис. 3.18, ж. При частоте 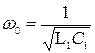кривая X(ω) пересекает ось абсцисс, а кривая b(ω) претерпевает разрыв от -∞ до + ∞. При этой частоте имеет место резонанс напряжений.

Если учесть, что при параллельном соединении элементов проводимости их надо сложить, то ясно, что для получения кривой b(ω) параллельно соединенных элементов необходимо сложить ординаты кривых b(ω) этих элементов. Зависимость b(ω) для схемы рис. 3.18 з изображена на рис. 3.18 к, а обратная ей зависимость Х(ω) - на рис. 3.18 и.

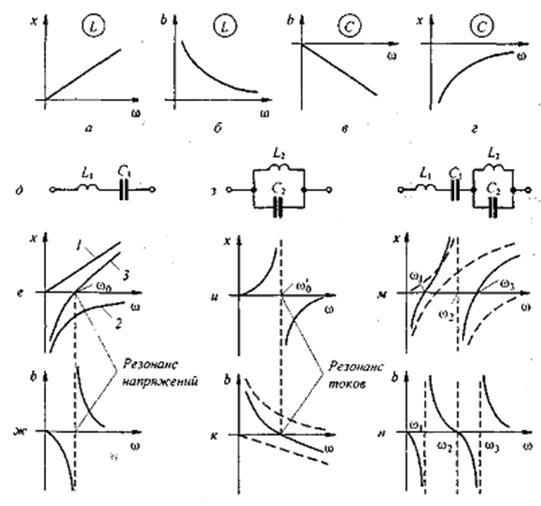
Рисунок 3.18

 

При частоте ω₀= 1/√ L₂ C₂ кривая b(ω) пересекает ось абсцисс, а X(ω) претерпевает разрыв от +∞ до -∞. При этой частоте имеет место резонанс токов в цепи (рис. 3.18 з). На рис. 3.18 л последовательно соединены два двухэлементных ранее рассмотренных двухполюсника. Так как Х(ω) каждого из них построена, то результирующее Х(ω) схемы на рис. 3.18 л получим, суммируя ординаты этих двухполюсников (т. е. кривых рис. 3.18 е,и). Зависимость Х(ω) для схемы на рис. 3.18 л приведена на рис. 3.18 м, а b(ω) - на рис. 3.18 н. При плавном увеличении частоты в схеме (рис. 3.18 л), начиная с ω = О, сначала возникает резонанс напряжений при частоте ω₁, затем резонанс токов при ω ₂, после этого резонанс напряжений при ω ₃. При дальнейшем увеличении ω резонансов возникать не будет.

Сделаем следующие выводы при плавном увеличении частоты ω:

1) режимы резонанса токов и резонанса напряжений чередуются;

2) число резонансных частот для канонических схем на единицу меньше числа реактивных элементов;

3) если в схеме есть путь для прохождения постоянного тока, то при плавном увеличении частоты, начиная с нуля, первым наступит резонанс токов, если нет - резонанс напряжений.

Это следует из того, что если есть путь для постоянного тока, то при ω = 0 характеристика X = f /(ω) начинается с нуля, затем X увеличивается (dX/dω >0), а при некоторой ω кривая претерпевает разрыв, который и соответствует резонансу токов. При аналитическом определении резонансных частот в реактивном двухполюснике сопротивление его следует представить в виде отношения двух полиномов по степеням ω, т.е. X = N (ω) / М (ω). Корни уравнения N(ω) = 0 соответствуют частотам, при которых возникает резонанс напряжений, корни уравнения М(ω) = 0 - частотам, при которых имеет место резонанс токов.

Расчет электрических цепей, содержащих источники энергии [источники ЭДС e (t)и источники тока j (t)] с несинусоидальной формой кривой, выполня­ется по методу положения. Процедуру расчета можно условно разделить на три этапа.

1)Гармонический анализ.

На этом этапе выполняется разложение несинусоидальных функций ис­точников ЭДС e (t)и источников тока j (t)в гармонический ряд Фурье:

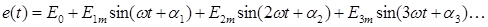
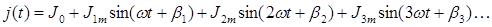
Для проведения анализа структуры функций e (t) и j (t)количество гармо­ник в их раз­ложении определяют значительно боль­ше, чем необходимо для расчета схемы.

2)Аналитический расчет.

Производится аналитический расчет схемы последовательно для каждой гармоники в отдельности. Для постоянной составляющей расчет производится как для резистивной цепи постоянного тока, при этом участки с катушками L закорачиваются, а ветви с конден­сато­рами C размыкается. Расчет схемы для от­дель­ных гармоник производится как для цепи си­нусои­дального тока, т.е. в ком­плексной форме, при этом определяются не действующие зна­чения, а ком­плексные амплитуды токов и напряжений (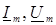). Расчет для каждой гармо­ники выпол­няется по одному и тому же алгоритму, при этом учитывается зави­симость реактивных со­противлений элементов от частоты и, следовательно, от номера гармо­ники: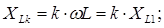 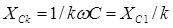. Выбор расчет­ного метода определяется структурой расчетной схемы.

Количество гармоник, для которых выполняется расчет схемы, устанав­ливается ис­ходя из конкретных условий задачи. Например, если определяются только действующие значения токов и напряжений (I, U), то достаточно учи­тывать только те гармоники, для ко­торых коэффициент 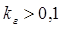, при этом от­но­сительная погрешность расчета в итоге не пре­высит 1%. Од­нако в тех слу­чаях, когда требуется проводить исследование форм кривых функций u (t) и i (t), то необходимо учи­тывать также гармоники более высокого порядка с меньшим коэффициентом гармоник .

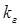3.Синтез решения.

На заключительной стадии расчета определяются искомые величины со­гласно усло­вию задачи.

Мгновенные значения токов и напряжений i (t)и u (t) определяются в соответствии с принципом наложения как алгебраической суммы мгновенных значений отдельных состав­ляющих, например:

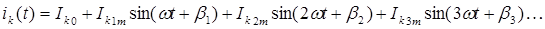
При необходимости исследования формы кривых функций i (t) и u (t) по полученным уравнениям строится их графические диаграммы.

Действующие значения токов и напряжений (I, U) находятся как средне­квадратич­ные значения этих функций по полученным ранее формулам, напри­мер:

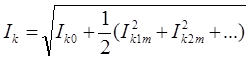
Активные мощности отдельных элементов определяется как суммы ак­тивных мощ­ностей этих элементов для отдельных гармоник, например:

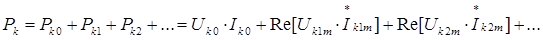
Активную мощность отдельных приемников можно определять также по формуле Джоуля: 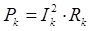, где 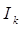-действующее значение тока этого при­емника.

Определяются коэффициенты исследуемых несинусоидальных функций: k_u - коэф­фициент искажения, k_ф -коэффициент формы k_г -коэффициенты от­дельных гармоник и т. д.

Равенство персеваля

Энергия сигнала u (t), выделяемая на резисторе с сопротивлением 1 Ом, определяется как

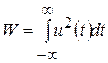. (4.14)

Выразим энергию сигнала u (t) через модуль его спектральной характеристики S (j Ω). Квадрат этого модуля представим в виде

,

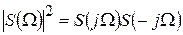где S (– j Ω) – функция, комплексно сопряженная с S (j Ω),

и проинтегрируем по частоте

.

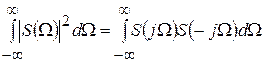Представим комплексно-сопряженную спектральную характеристику S (– j Ω) с помощью прямого интегрального преобразования Фурье (4.3) через сигнал u (t)

.

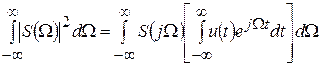Поменяем порядок интегрирования и сравним в новом выражении сомножитель в квадратных скобках с (4.4)

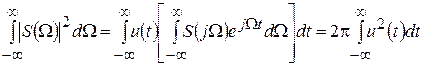. (4.15)

Из сравнения (4.14) и (4.15) получим

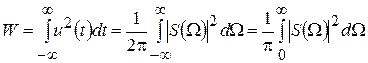. (4.16)

Соотношение (4.16) называют равенством Парсеваля или теоремой Рейли. Из этого соотношения следует, что энергию непериодического сигнала за время его существования можно определить, интегрируя квадрат модуля спектральной характеристики этого сигнала.

Спектральная характеристика одиночного прямоуголного сигнала.
В связи с тем, что одиночный прямоугольный видеоимпульс (рис. 1.29) может быть представлен следующим образом

Рис.1.29

,

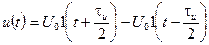то, используя свойство аддитивности преобразований Фурье, которое заключается в том, что если

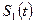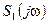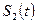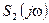≓ , ≓ и т. д., то

≓

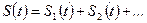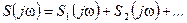
а также свойство сдвига аргумента состоящее в том, что если

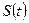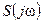≓ , то ≓ ,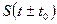

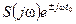получим:

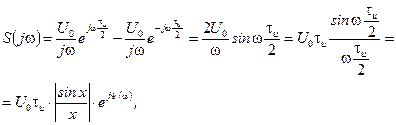
где 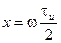, а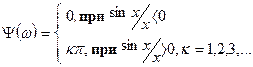

Аналогичное выражение для 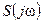одиночного прямоугольного видеоимпульса получим, применяя интеграл Фурье

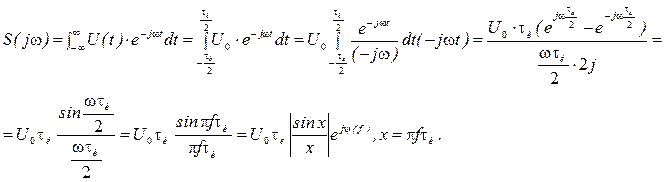
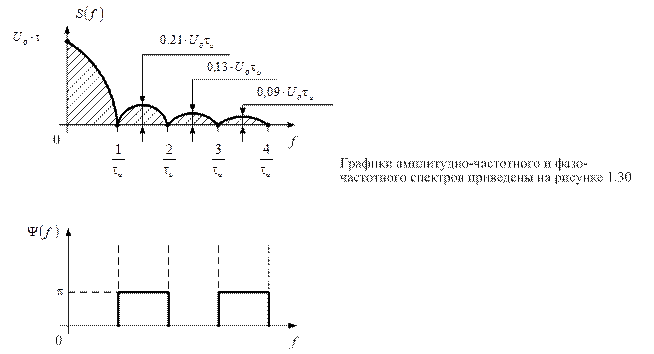
Рис.1.30

Спектральная плотность зависит от частоты в соответствии с функцией

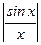
Максимальное значение спектральной плотности при .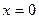

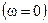Нулевые значения спектральной плотности будут иметь место на частотах 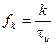, т.к. функция 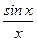проходит через ноль, когда 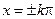, где 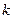= 1.2.3,.... т.е. на частотах

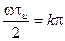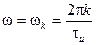, или .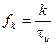

Ширина спектра сигнала, определяемая на уровне 90% энергии сигнала (Э_с) равна 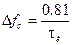. База сигнала .

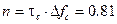График ФЧС построен исходя из следующих соображений. Положительным значением 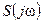соответствуют начальные фазы, равные нулю, а отрицательным - начальные фазы, равные .

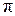Для оценки влияния длительности импульса на его спектр сравним АЧС импульсов разной длительности и одинаковой амплитуды. Длительность первого импульса 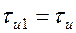, второго .

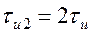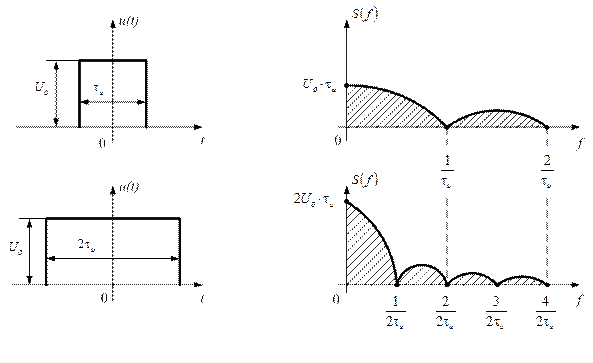
Рис. 1.31

Из анализа графиков рисунка 1.31 следует, что удлинению импульса в 2 раза соответствует сужение графика АЧС, при этом ширина спектра уменьшается в 2 раза 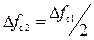, максимальное значение 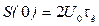пропорционально длительности импульса и увеличивается в 2 раза.

Для запаздывающего импульса, показанного на рисунке 1.6, спектральная плотность в соответствии с полученным выше результатом и теоремой о сдвиге аргумента будет

≓

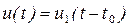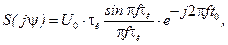
то есть при неизменном АЧС ФЧС определяется выражением

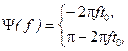
График ФЧС при 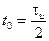показан на рисунке 1.32

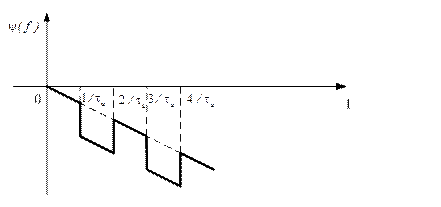
Рис.1.32