Дифференциальные уравнения.
Тема урока: Дифференциальные уравнения первого порядка.
Дифференциальные уравнения с разделяющимися переменными.
Цели урока:
- помочь усвоить понятие дифференциальное уравнение;
- помочь овладеть методами решения ДУ;
- отработать навыки решения дифференциальных уравнений первого
порядка.
План урока:
1. Объяснение нового материала.
2. Закрепление изученного материала.
3. Информация о домашнем задании.
Ход урока
1. Объяснение нового материала:
Мотивация: Решить уравнение: у'=2х.
Что содержит данное уравнение?
у'=2х.- дифференциальное уравнение (ДУ).
Дифференциальные уравнения (ДУ) обычно кажутся чем-то запредельным и трудным в освоении многим студентам, но на самом деле ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ – ЭТО ПРОСТО И ДАЖЕ УВЛЕКАТЕЛЬНО.
Теоретическая часть:
Определение 1:
Дифференциальные уравнения – это уравнения, содержащие искомые функции, их производные различных порядков и независимые переменные.
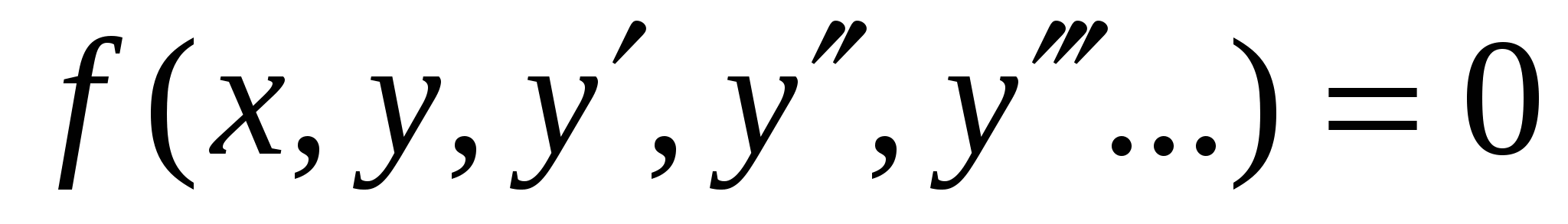
Определение 2:
Порядком дифференциального уравнения называется наивысший порядок, входящих в него производных.
Примеры:
ху'+у=0- дифференциальное уравнение первого прядка.
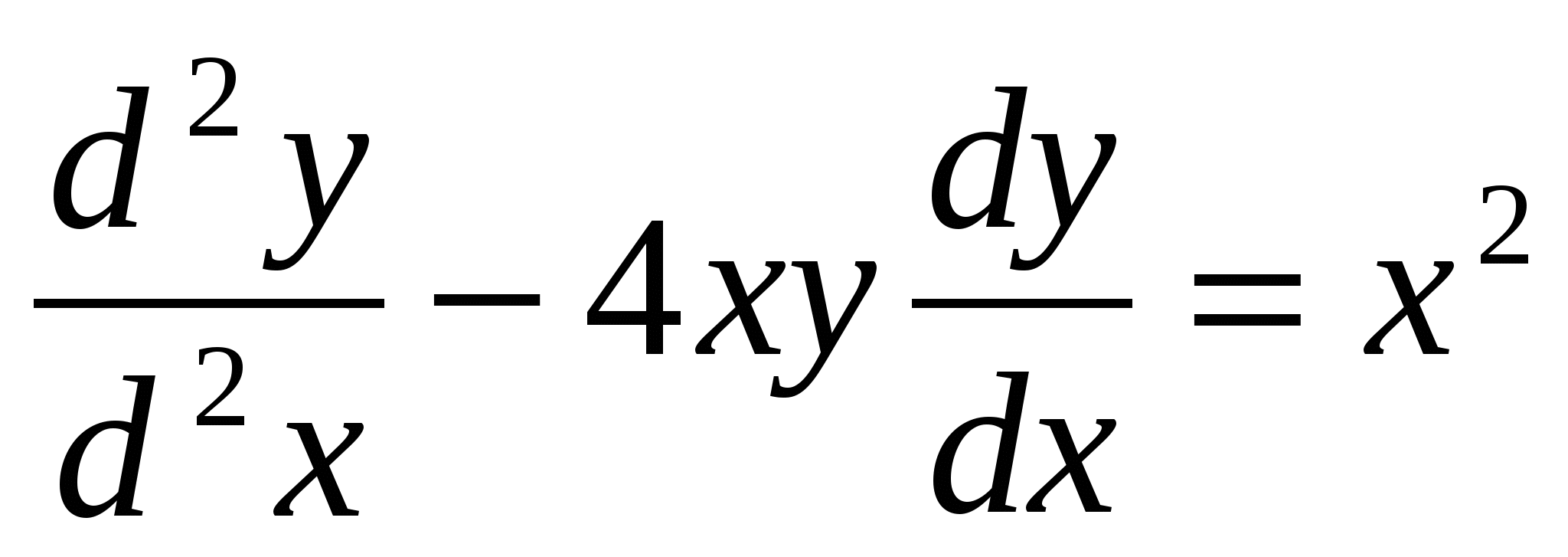 - дифференциальное уравнение 2-го порядка.
- дифференциальное уравнение 2-го порядка.
у'''-2у=х- дифференциальное уравнение третьего порядка.
Определение 3:
Решить дифференциальное уравнение – это значит, найти множество функций
y = f (x) + C, которые удовлетворяют данному уравнению.
Такое множество функций называется общим решением дифференциального уравнения.
Определение 4:
Дифференциальным уравнением 1-го порядка с одной неизвестной функцией называется соотношение F (x, у, у') = 0 между независимой переменной х, искомой функцией у и еѐ производной.
Дифференциальное уравнение первого порядка в общем случае содержит:
1) независимую переменную 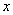 ;
;
2) зависимую переменную 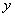 (функцию);
(функцию);
3) первую производную функции: 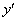 .
.
В некоторых уравнениях 1-го порядка может отсутствовать «икс» или «игрек», но это не существенно – важно чтобы в ДУ была первая производная 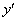 , и не было производных высших порядков –
, и не было производных высших порядков – 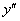 ,
, 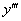 и т.д.
и т.д.
Определение 6
Частное решение дифференциального уравнения — это решение, не содержащее произвольных постоянных.
Определение 7: Частным решением ДУ называется решение, полученное из общего при различных числовых значениях произвольных постоянных.
Значения произвольных постоянных находятся при определенных начальных значениях аргумента и функции.
Определение 8: Задача, в которой требуется найти частное решение ДУ, удовлетворяющее начальному условию у(х0)=у0, называется задачей Коши.
(Огюстен Луи Коши(1789-1857)- французский математик).
Пример 1. у'=2х. С чего начать решение?
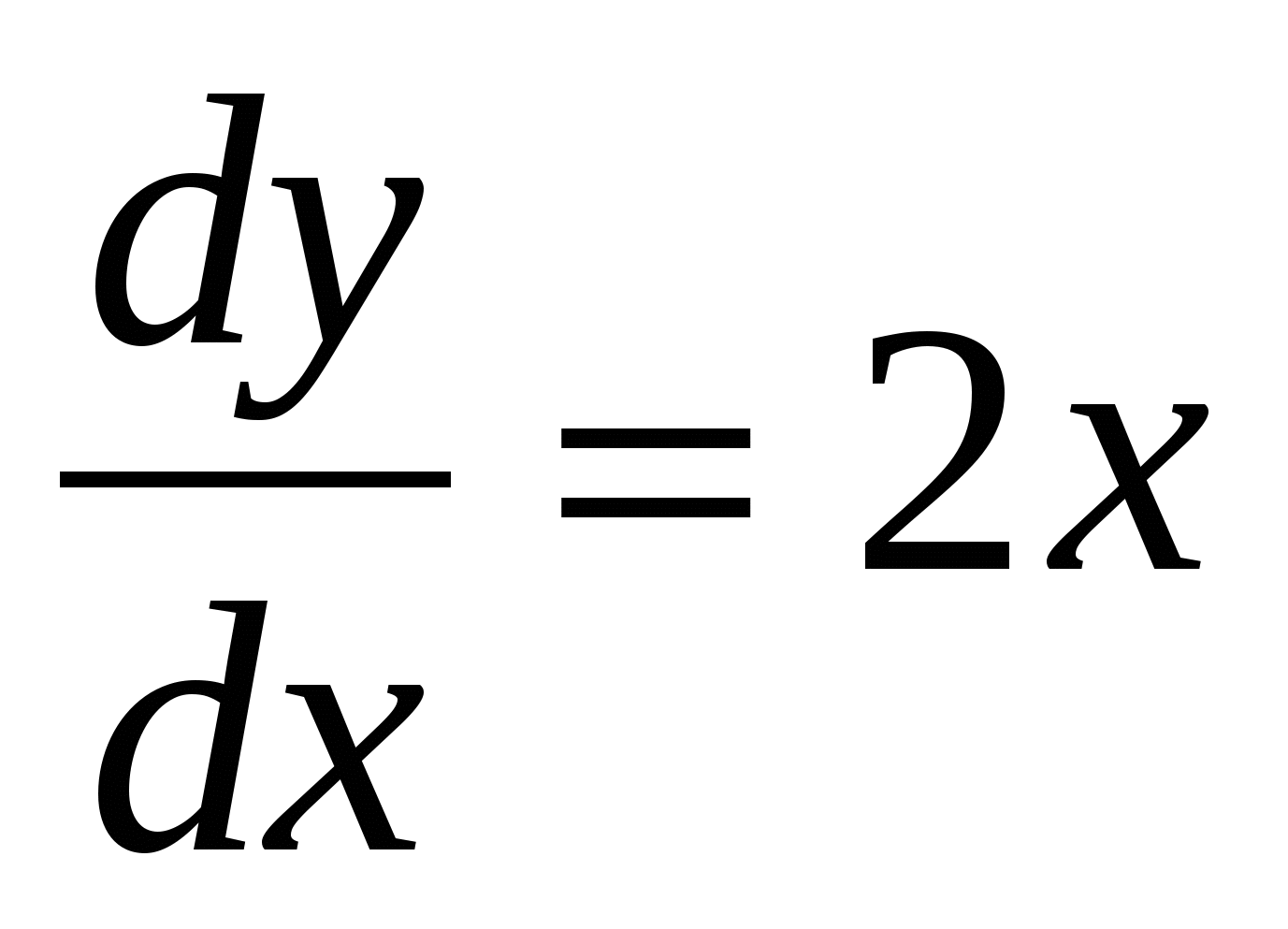 ,
,
На втором шагесмотрим, нельзя ли разделить переменные?
Разделим переменные
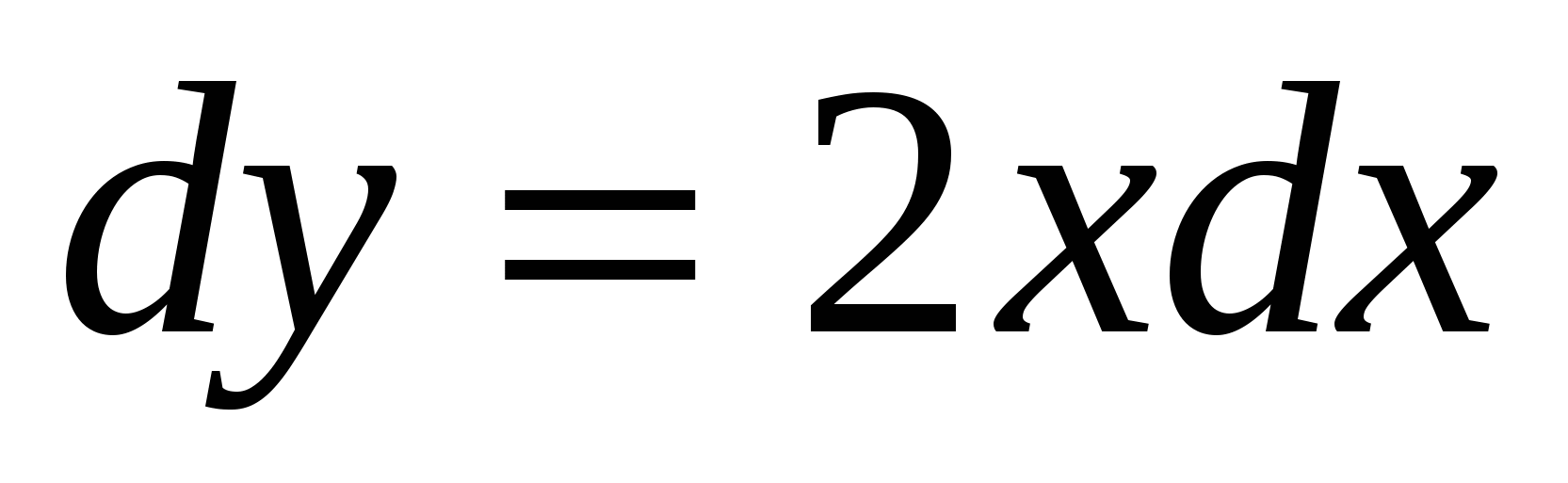
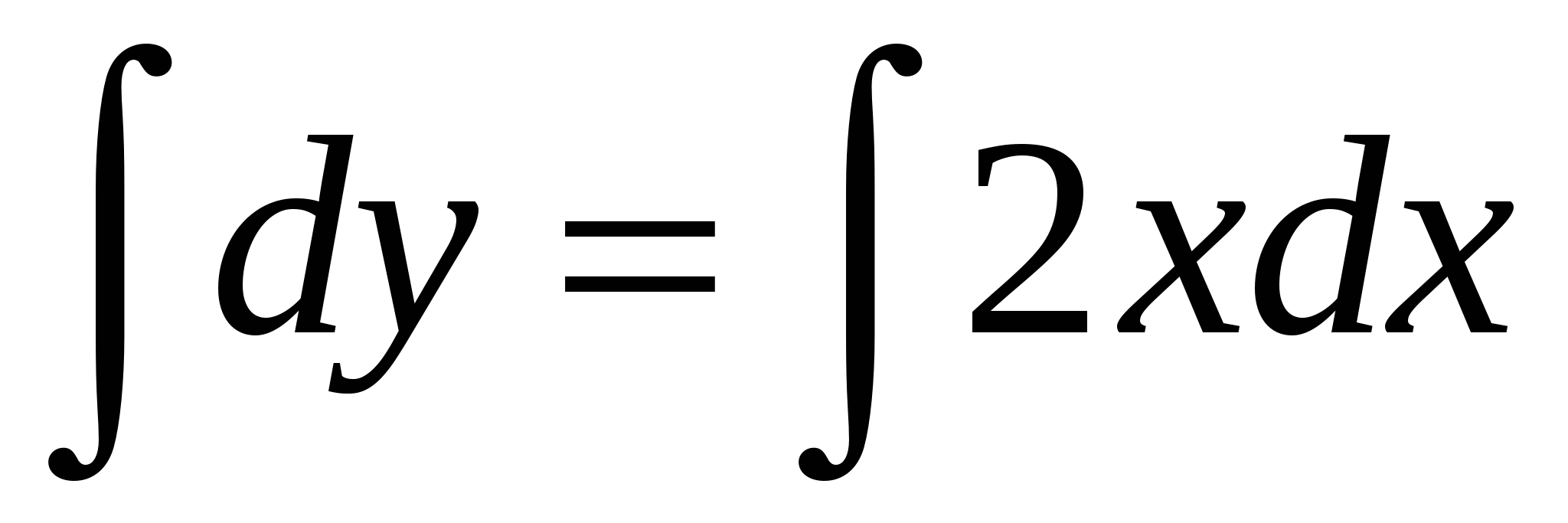 ,
,
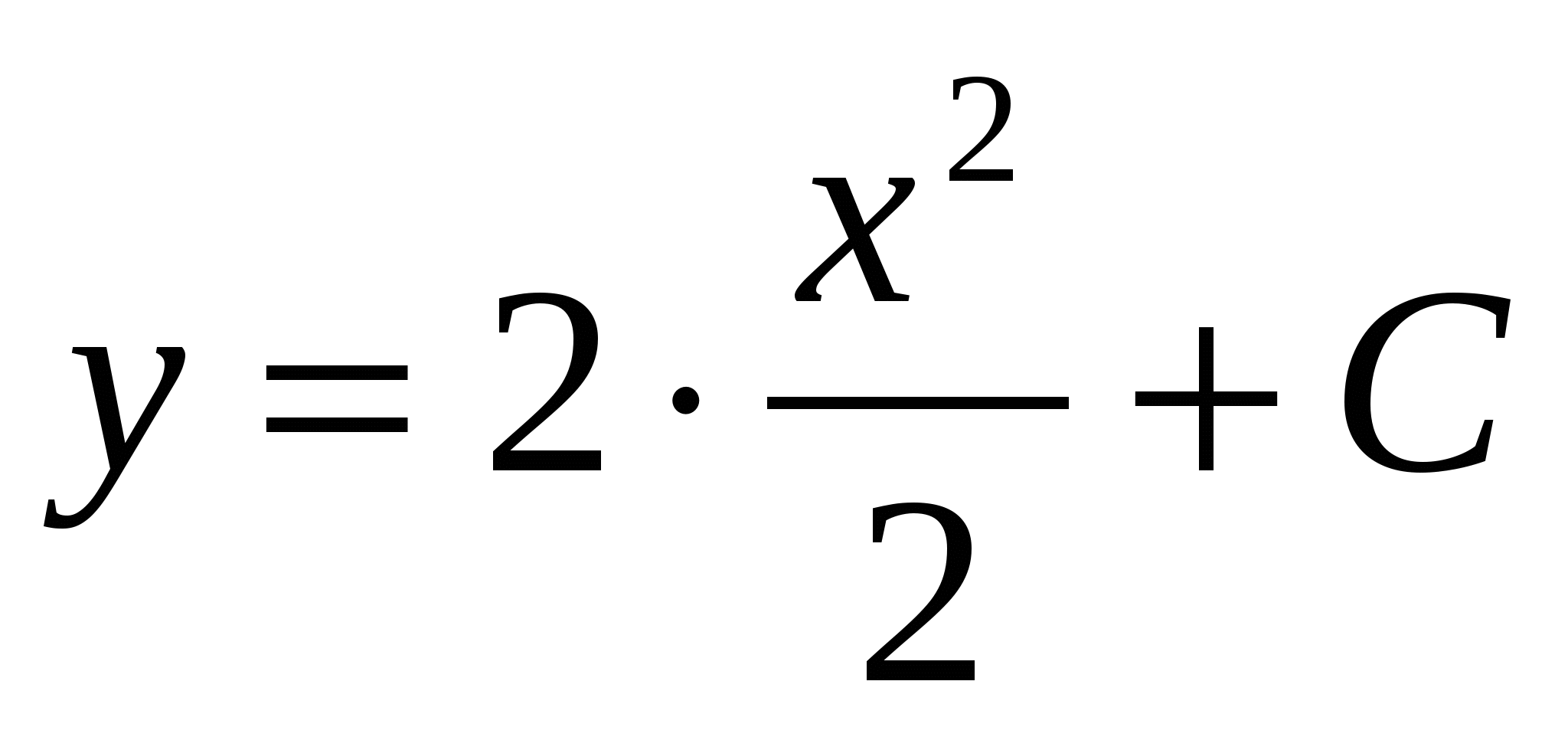
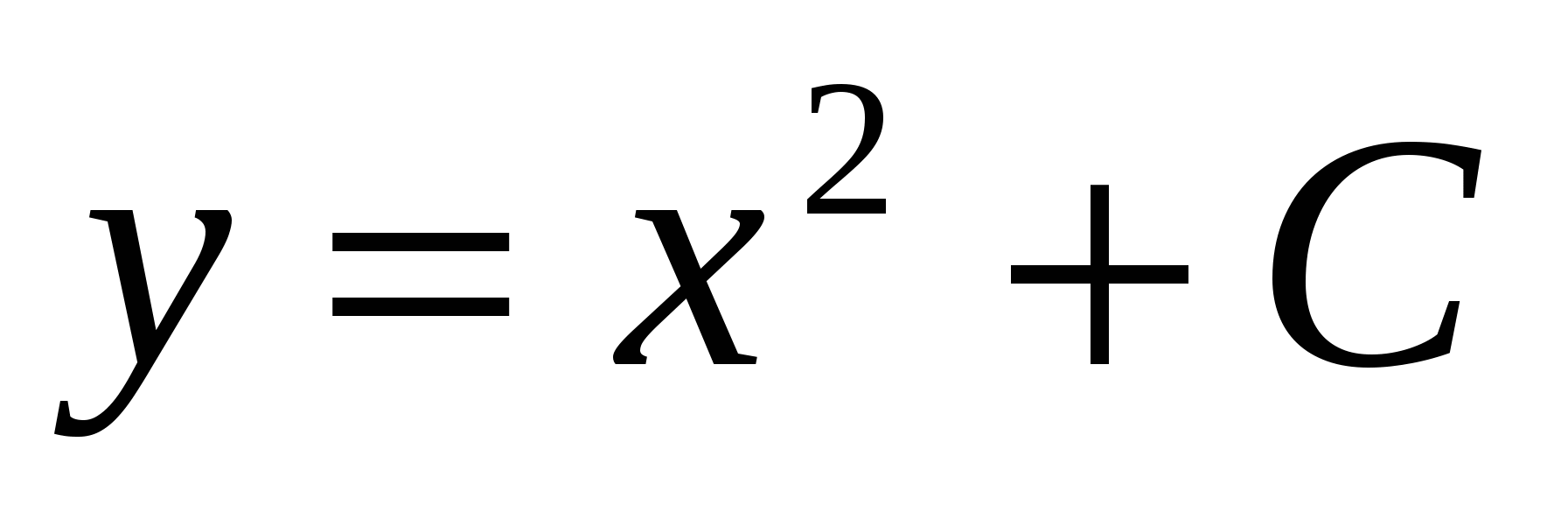 - общее решение
- общее решение
2) При х= 2, у=5, тогда
5= 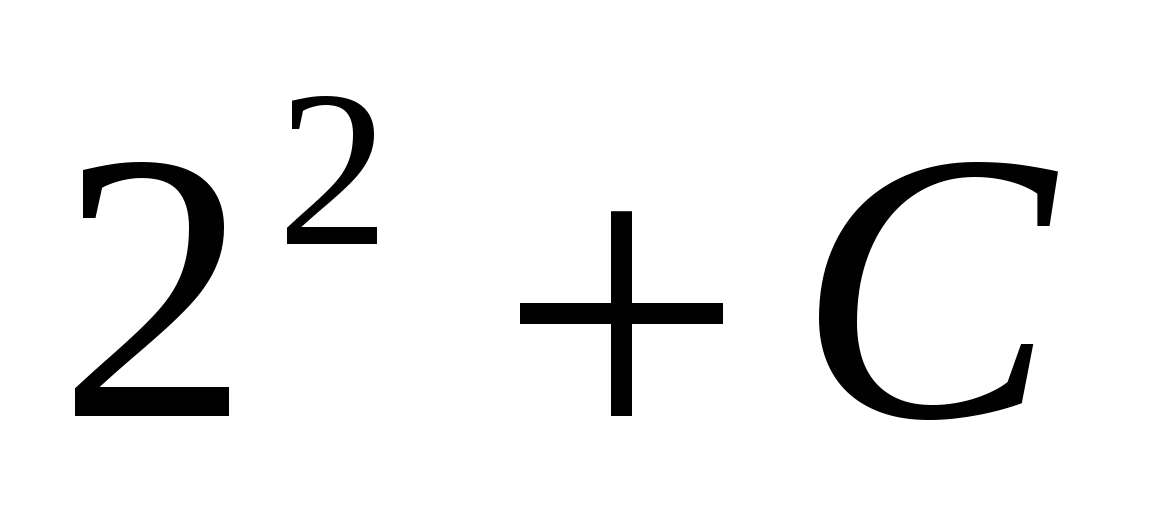 , 5= 4+с, получим
, 5= 4+с, получим
с= 1, следовательно,
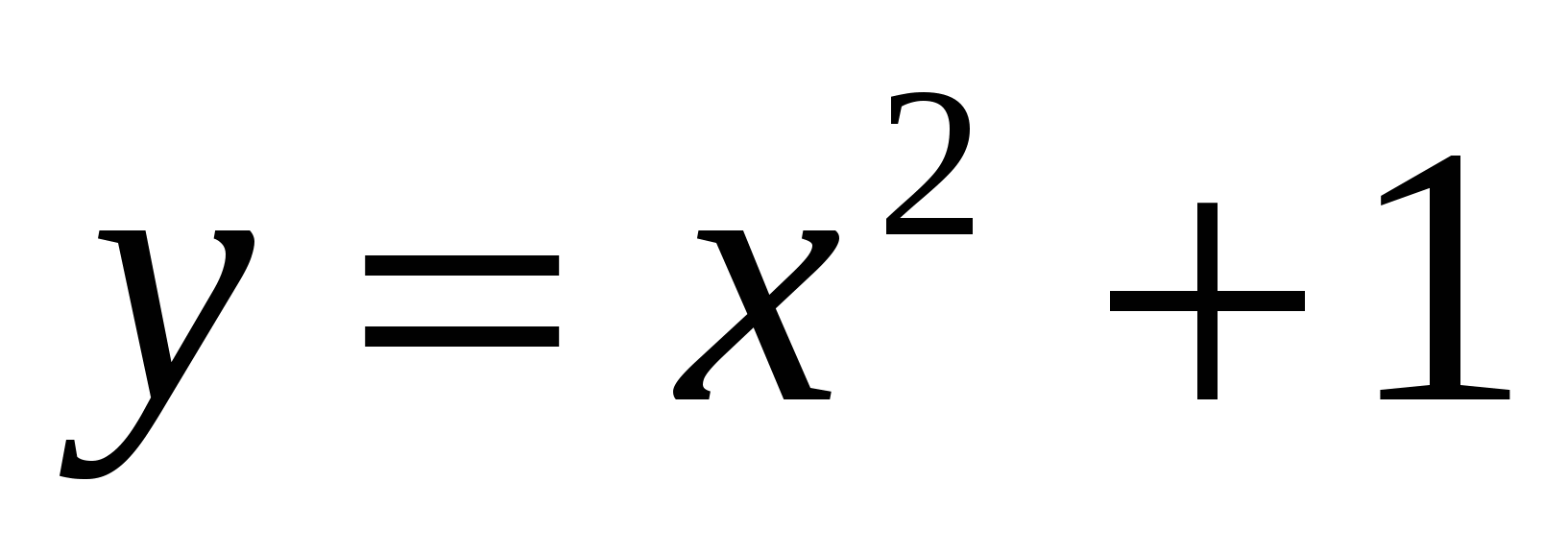 - частное решение.
- частное решение.
Мы сначала рассмотрим самые простые ДУ – это ДУ с разделяющимися переменными.
Определение 9: Дифференциальные уравнения f(y) dy = g(x) dx называют уравнениями с разделенными переменными
Определение 9-1: Линейное уравнение первого порядка – это уравнение вида:
Линейное уравнение первого порядка в стандартной записи имеет вид:
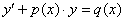
Определение 10: Если q(x) = 0, то уравнение называется однородным, если q(x) ≠ 0, то уравнение неоднородное
Для решения этого уравнения необходимо:
1. Переписать производную
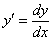
2.разделить переменные;
проинтегрировать обе части полученного равенства.
Пример2: Решить дифференциальное уравнение 
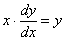
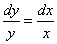
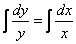
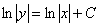
Единственное, у нас «игрек» не выражен через «икс», то есть решение представлено в неявном виде.
Определение 11
Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.
Давайте попытаемся получить общее решение.
Пожалуйста, запомните первый технический приём, он очень распространен и часто применяется в практических заданиях: если в правой части после интегрирования появляется логарифм, то константу во многих случаях (но далеко не всегда!) тоже целесообразно записать под логарифмом.
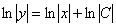 Используем свойство логарифмов
Используем свойство логарифмов 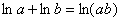
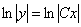
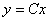 - представлена в явном виде
- представлена в явном виде
Пример 3:
1)
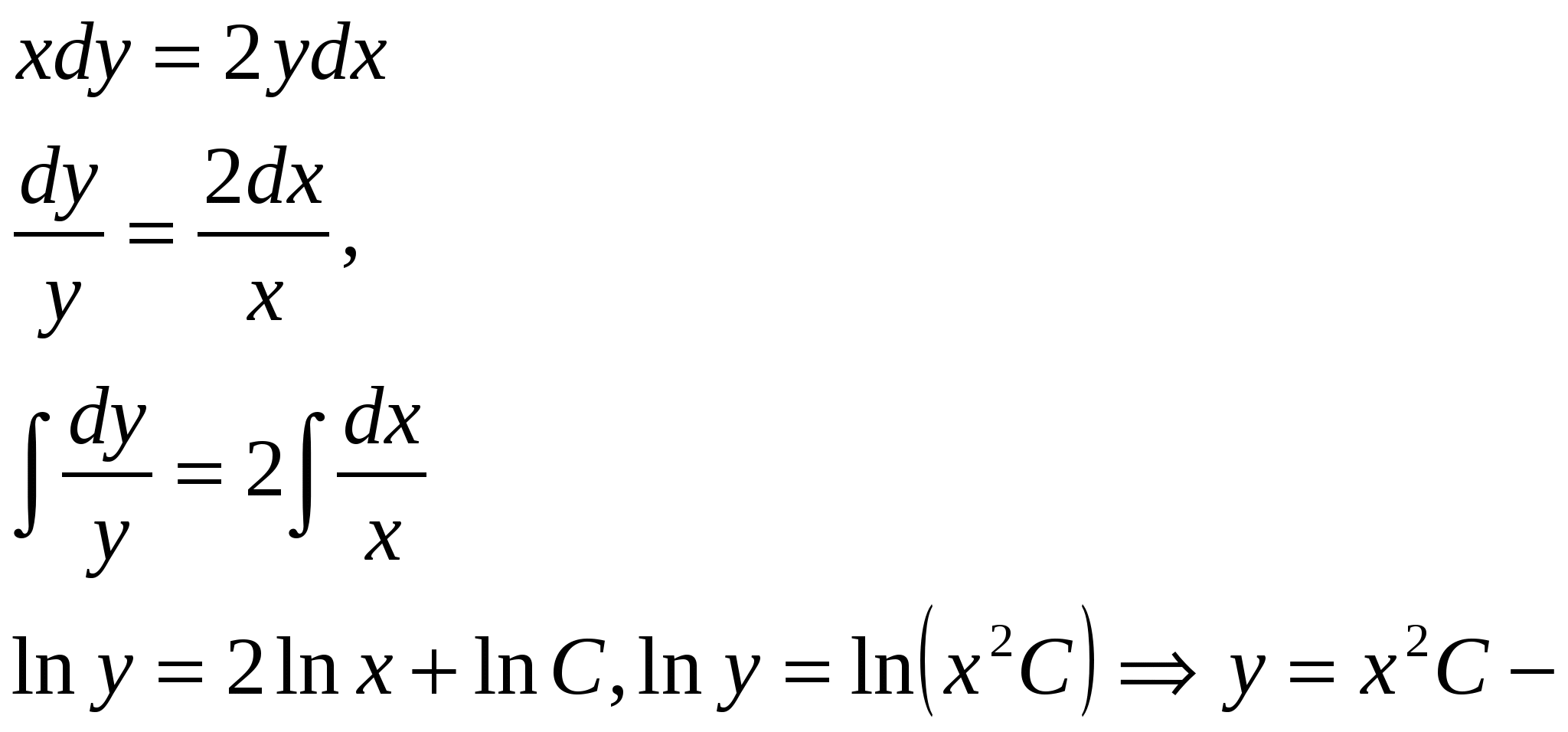
Общее решение.
2) 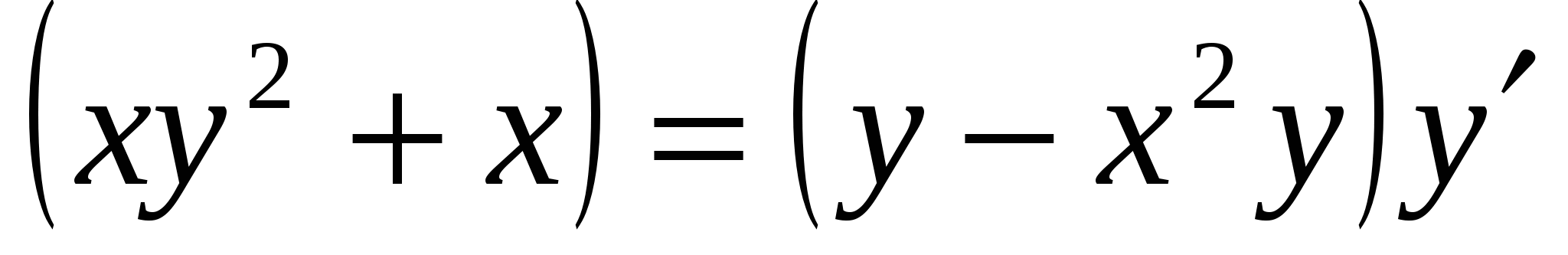 ,
,
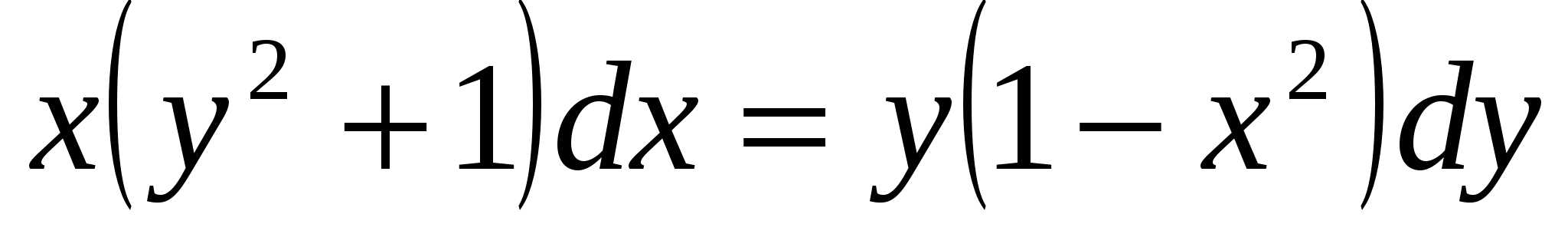
, 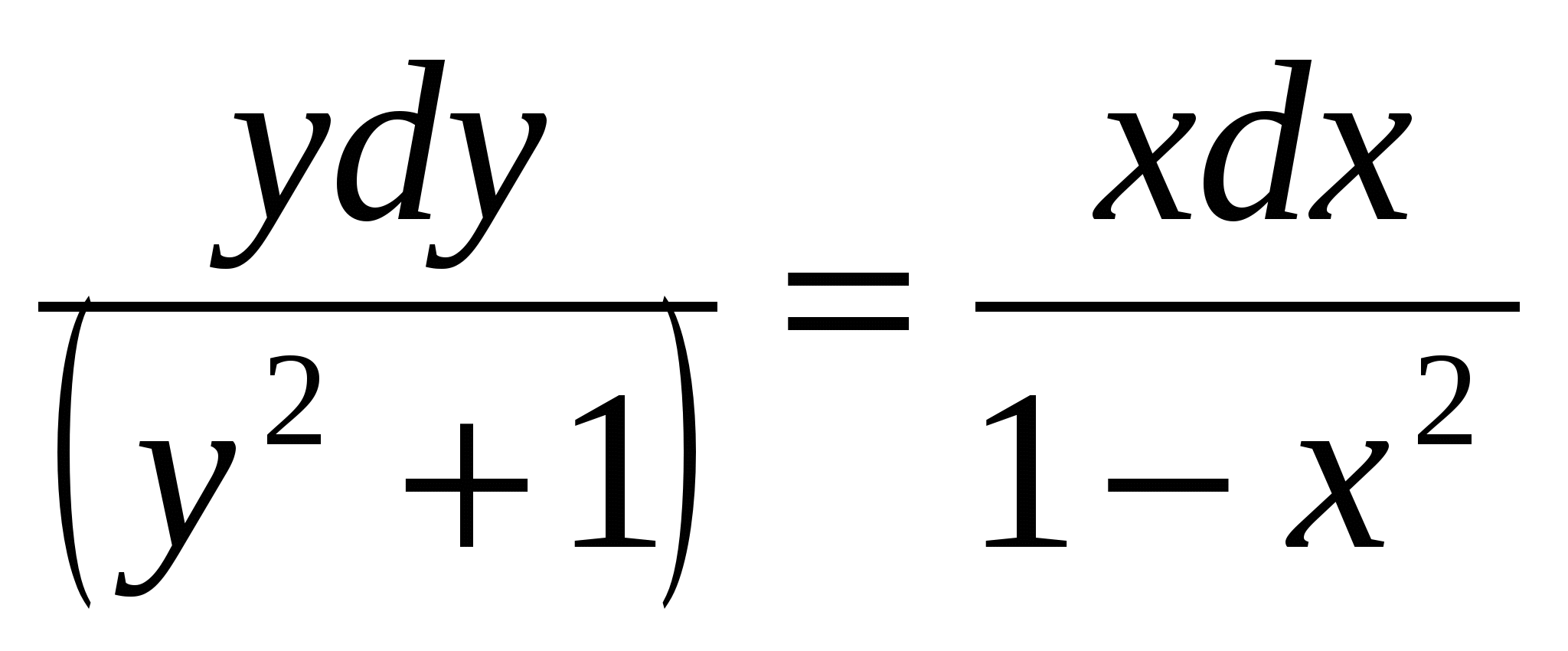
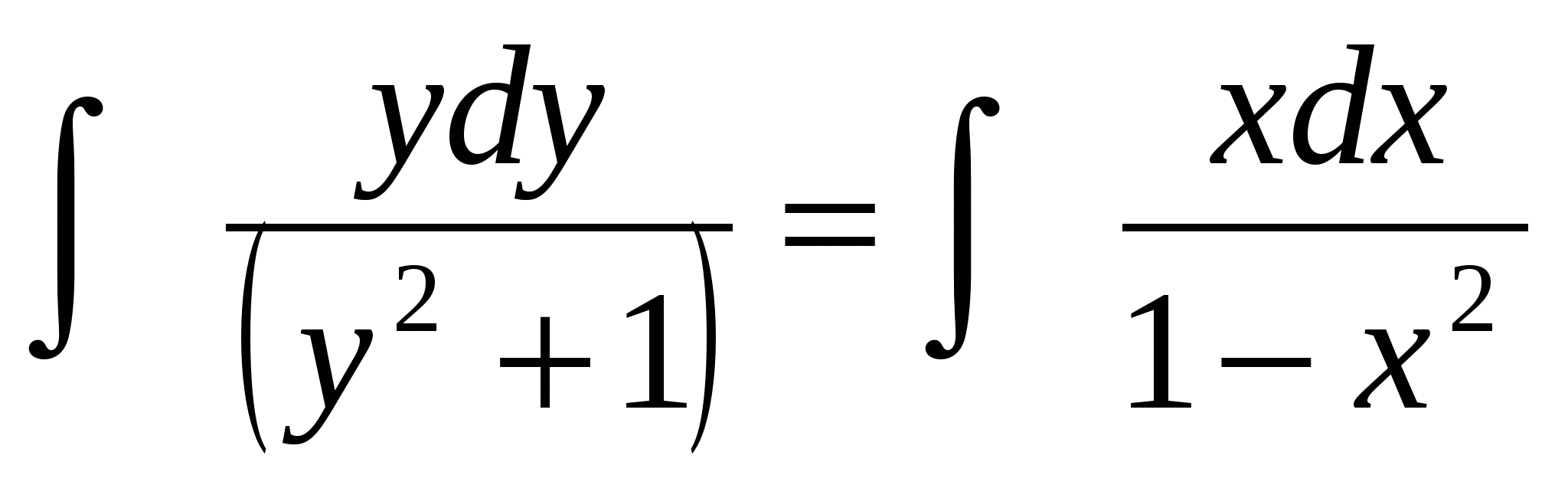 ,
,
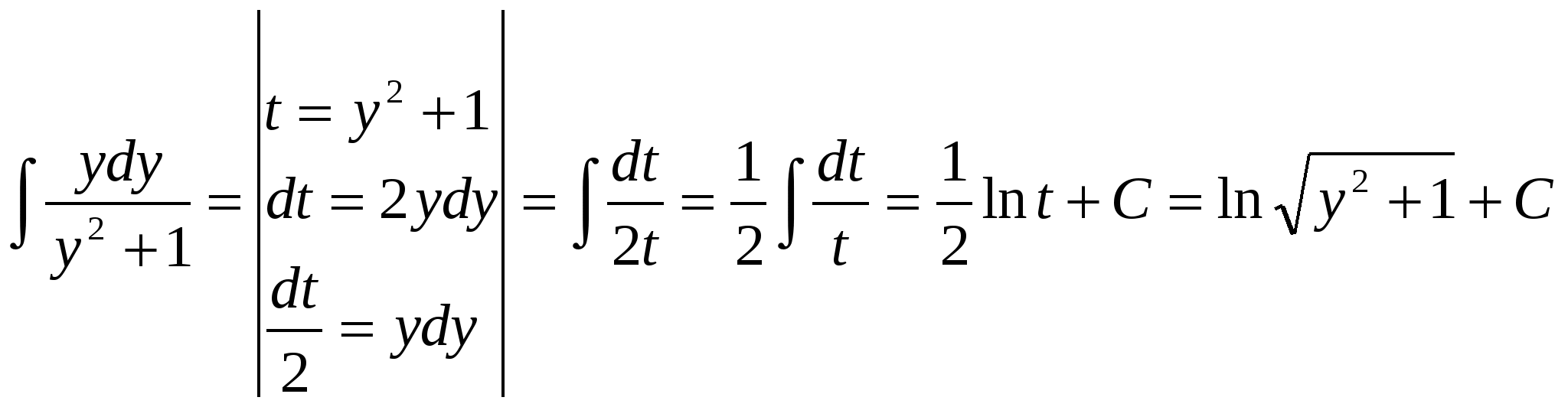

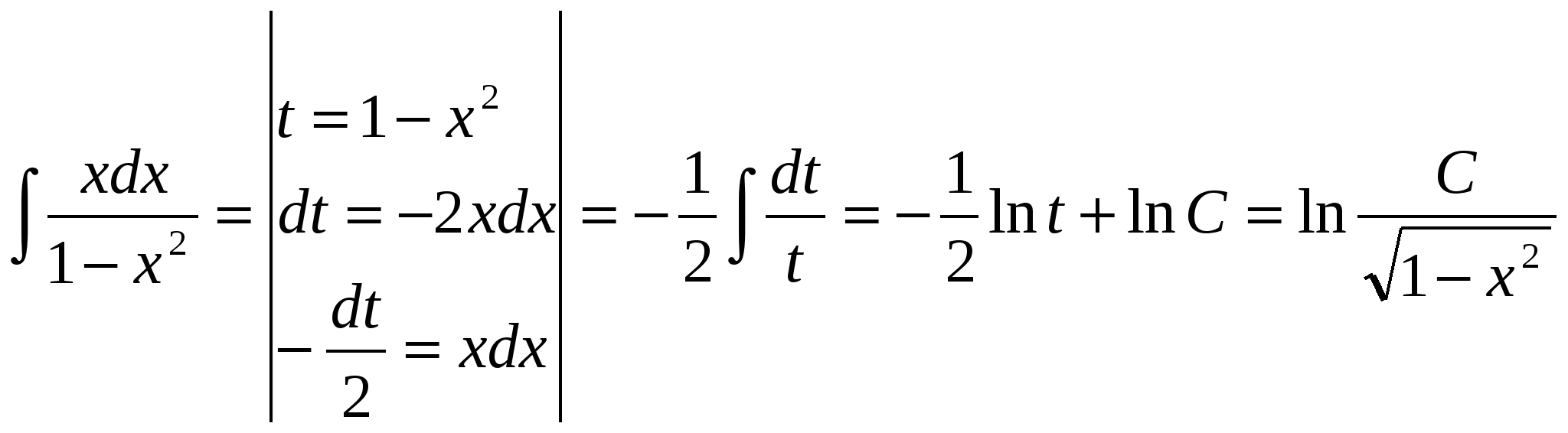 ,
,
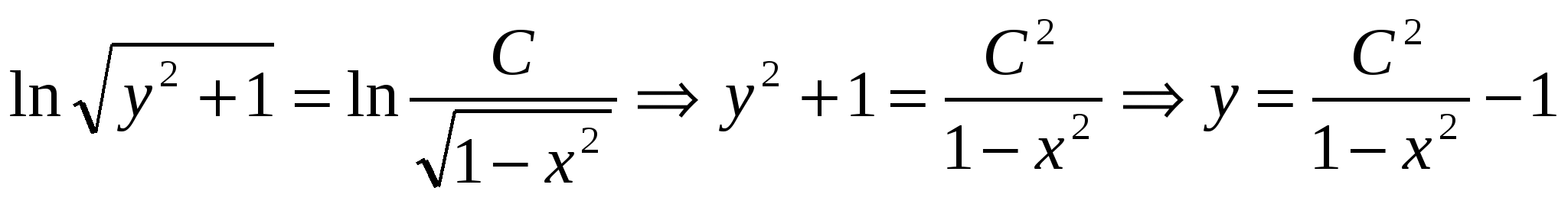 -общее решение
-общее решение
Найдем частное решение при начальных условиях: при х=2, у=-4.
Получим: -4+1=С2/(-3), тогда С2=9.
Частное решение имеет вид: 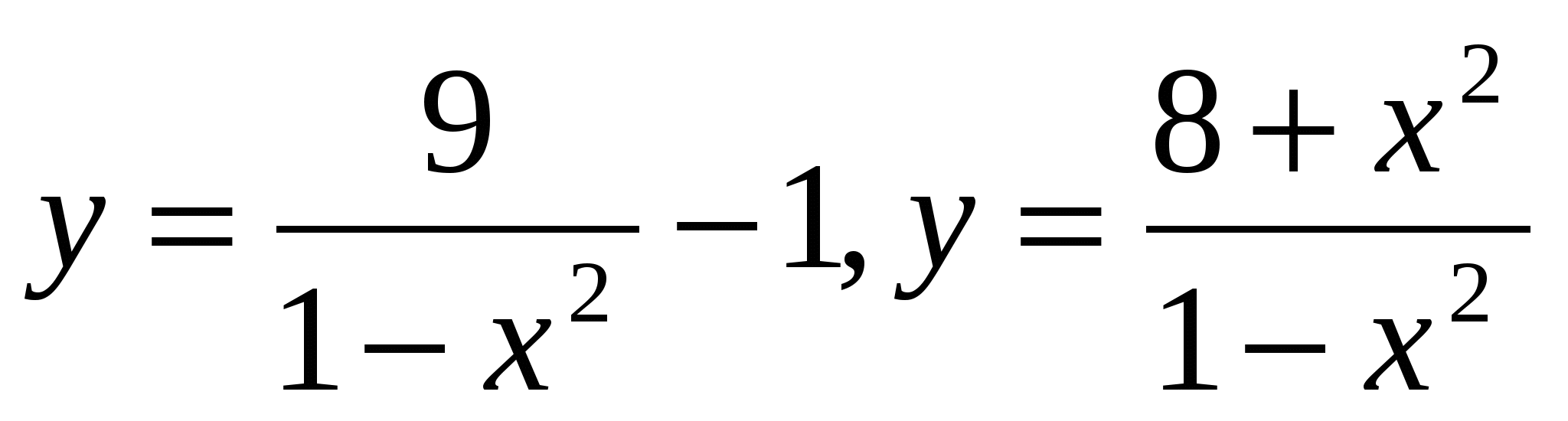 .
.
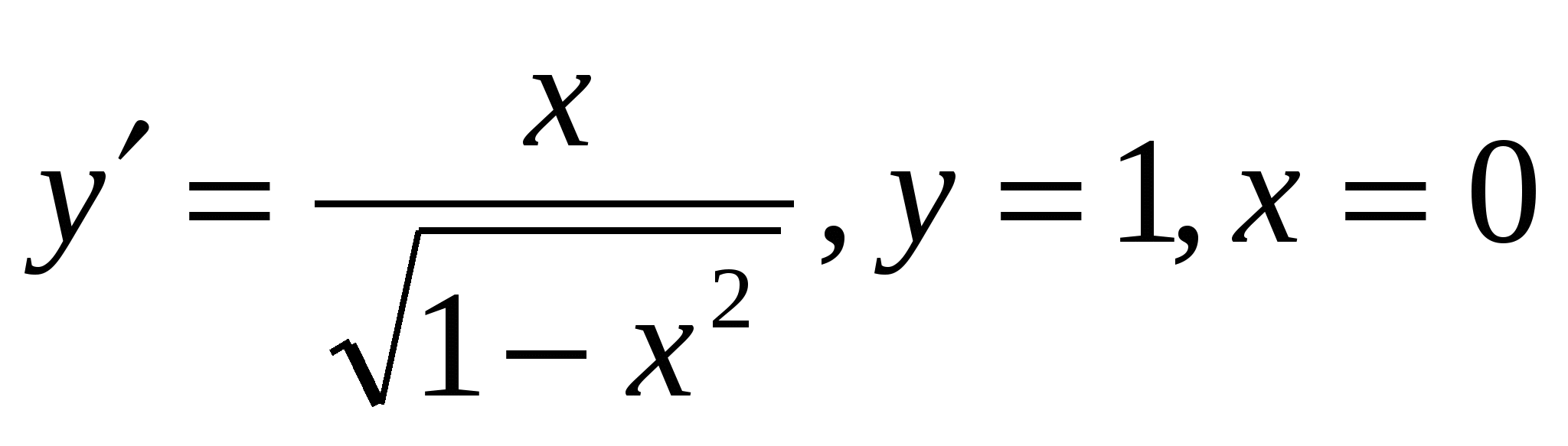
Пример 4. Найти общее решение дифференциального уравнения
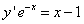 .
.
Это уравнение с разделяющимися переменными. Решение. Для разделения переменных поделим обе части уравнение на 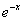 и получим
и получим
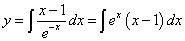 .
.
Чтобы найти y, требуется найти интеграл. Интегрируем по частям.
Пусть 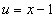 ,
, 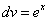 .
.
Тогда 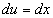 ,
, 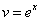 .
.
Находим общее решение уравнения:
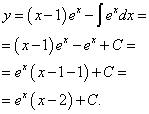
2.Закрепление:
Решить примеры.
у'=4х3.Найти общее решение.(ответ: у=х4+С)
1. 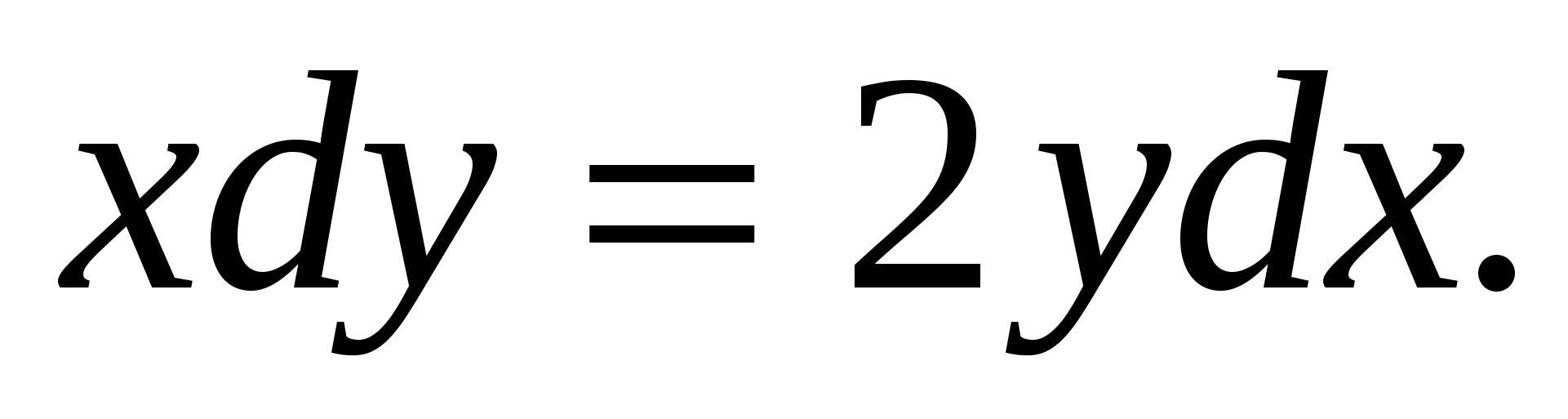 (ответ:
(ответ: 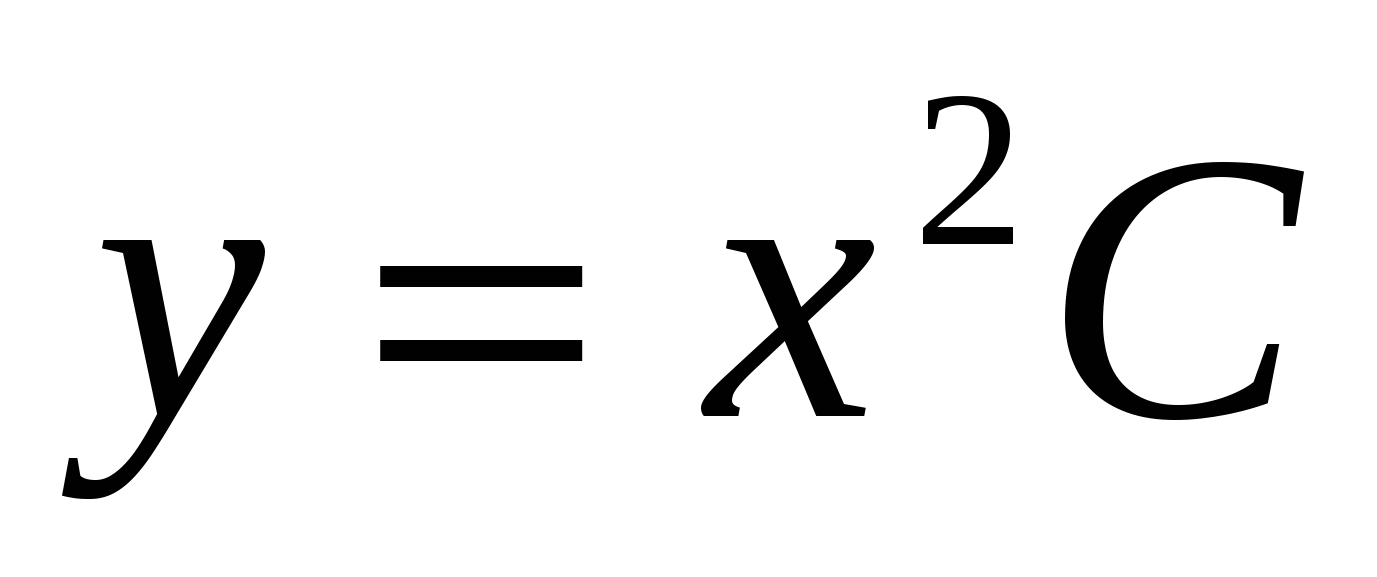 )
)
Найти частные решения ДУ:
3. 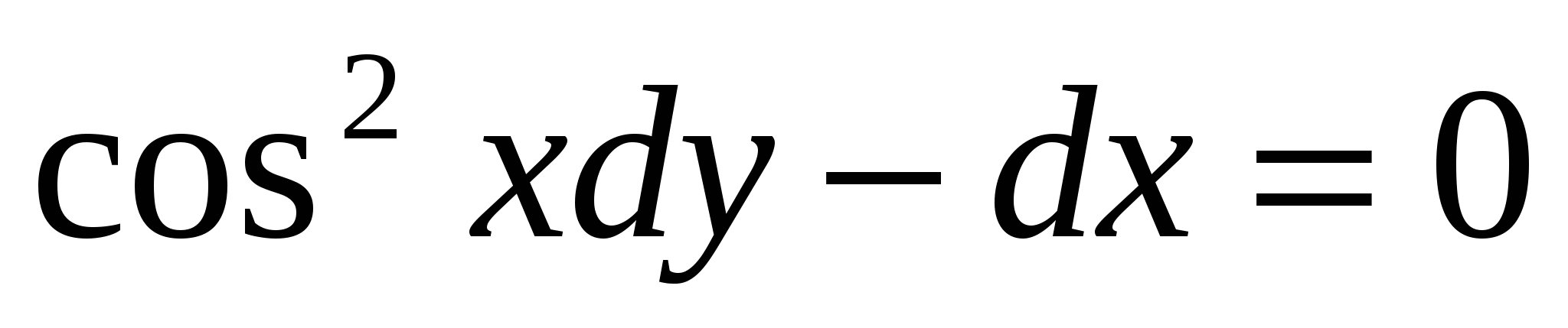 , при х=
, при х= 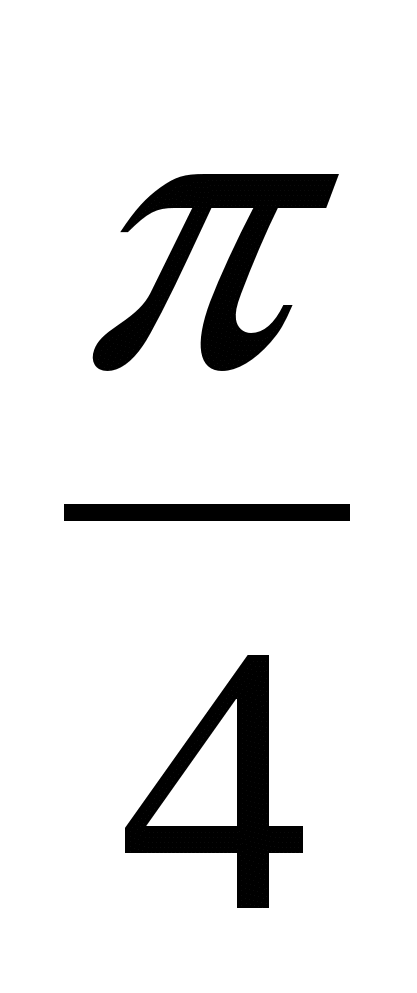 , у=3(ответ: y=tgx+2)
, у=3(ответ: y=tgx+2)
4. 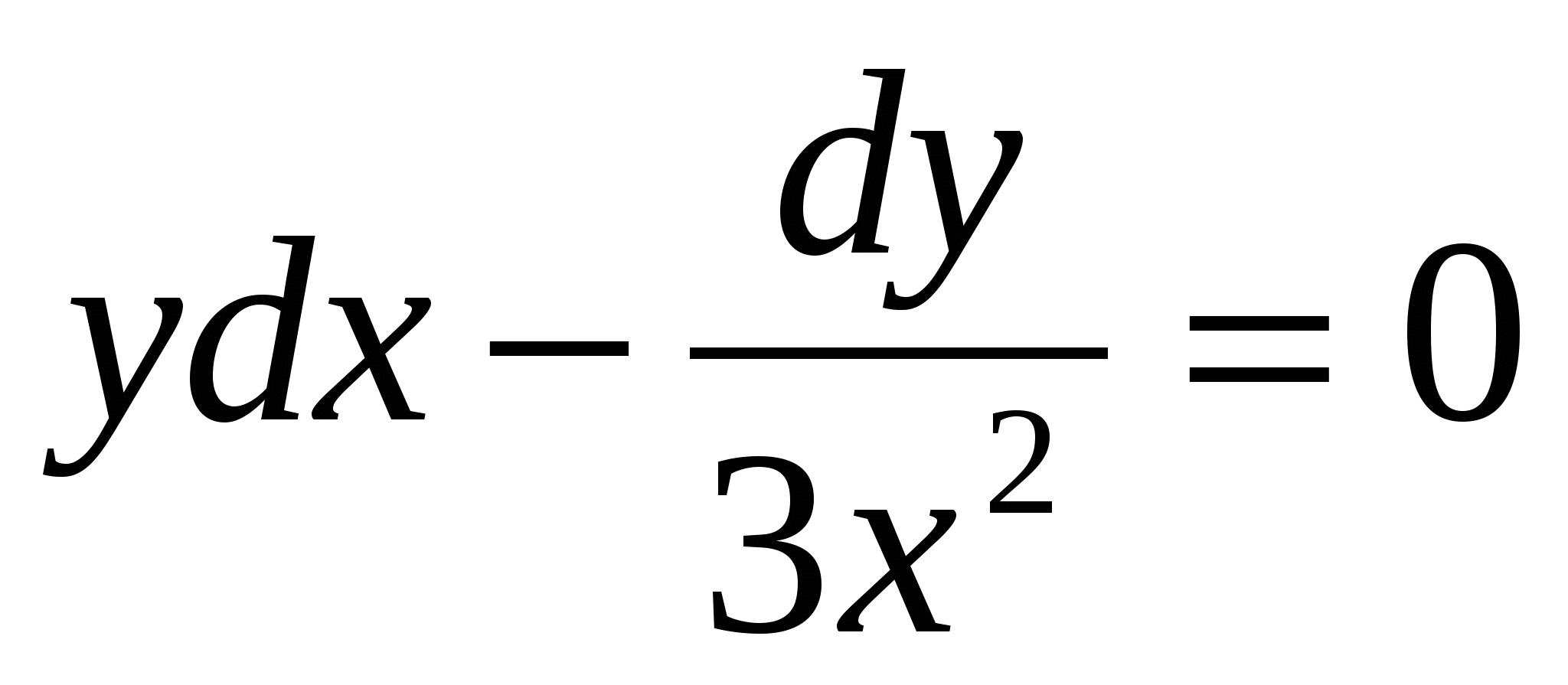 , при х=0, у=1 (ответ:
, при х=0, у=1 (ответ: 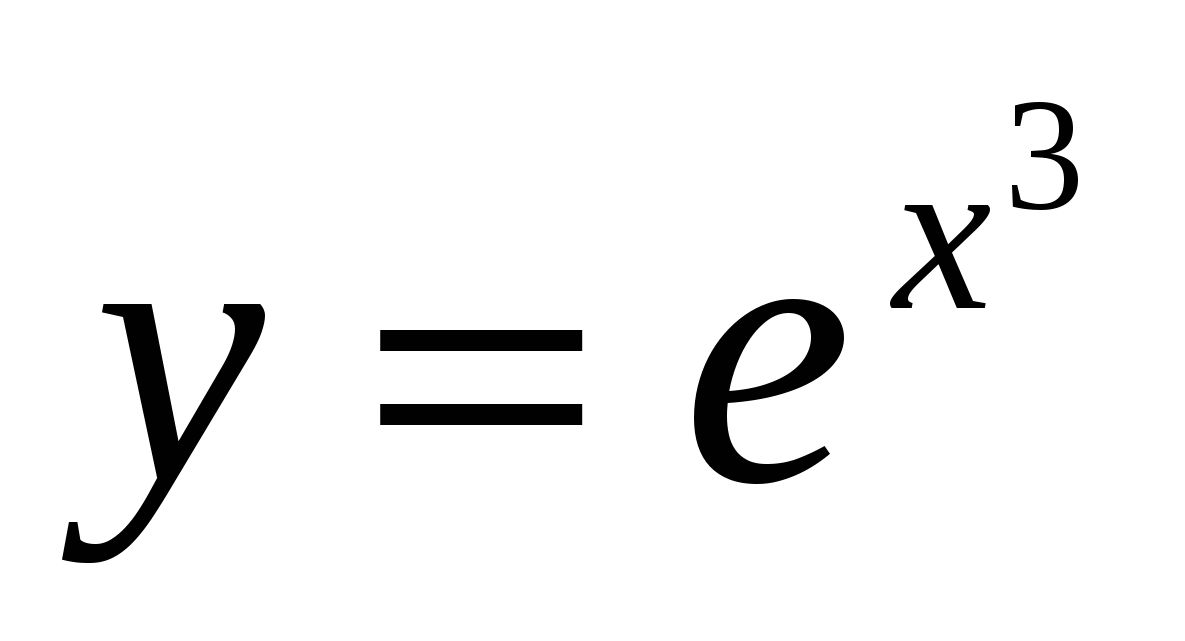 )
)
5. 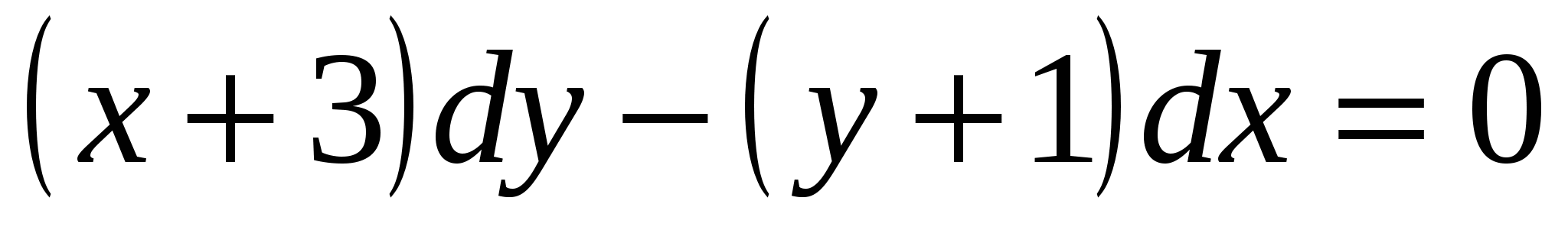 ,
, 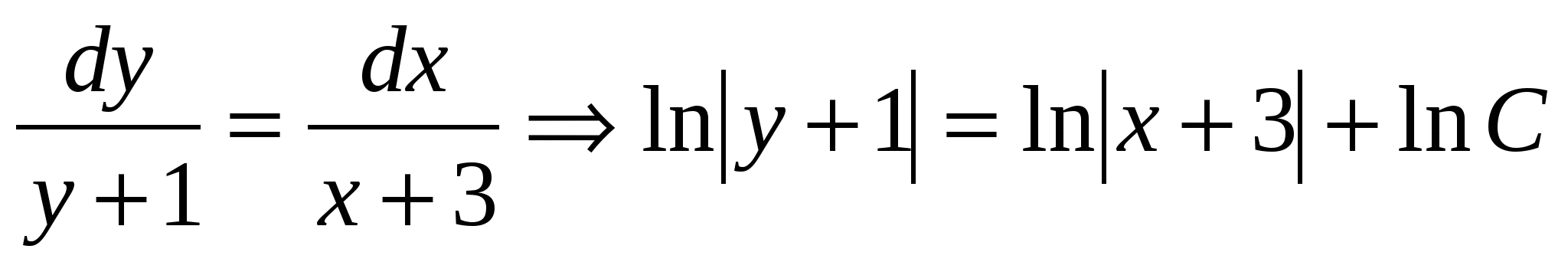 ,
,
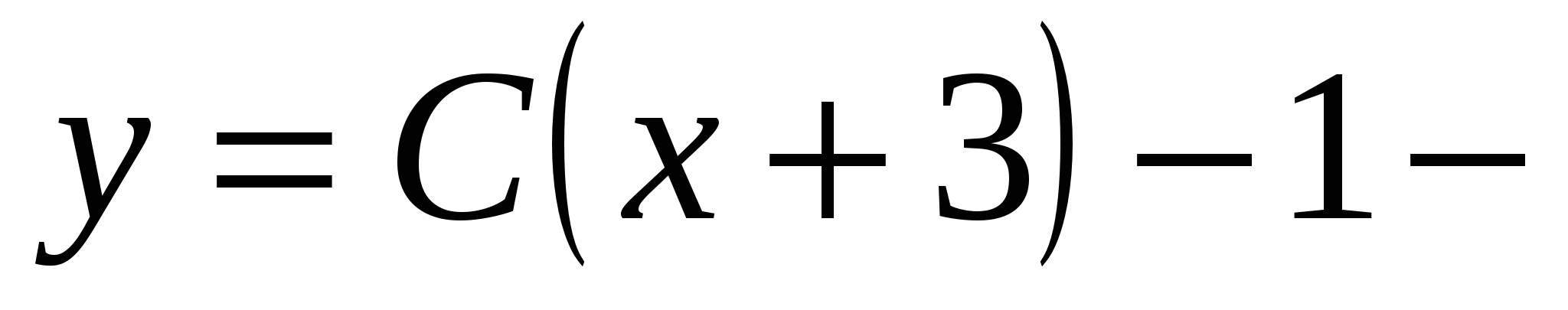 общее решение.
общее решение.
6. Найти частное решение ДУ 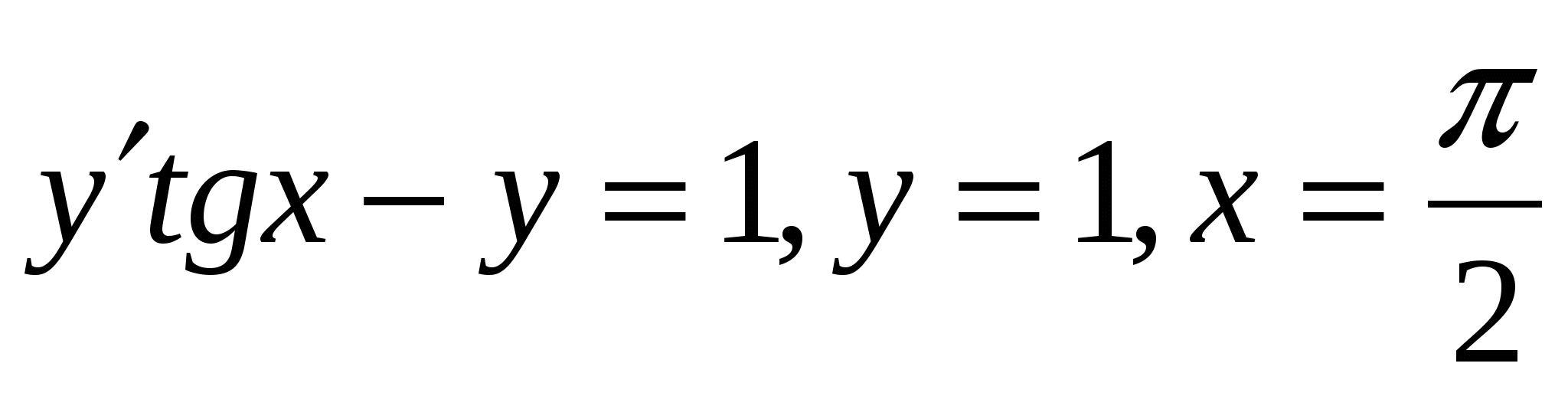 .
.
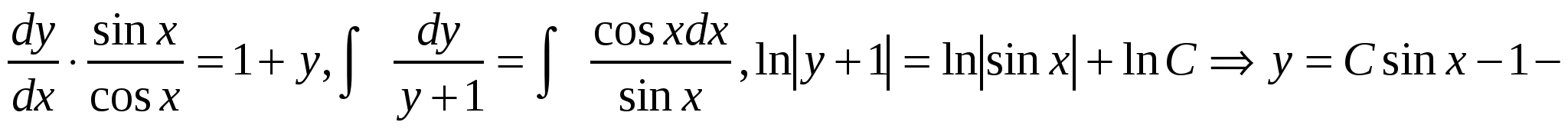 общее решение.
общее решение.
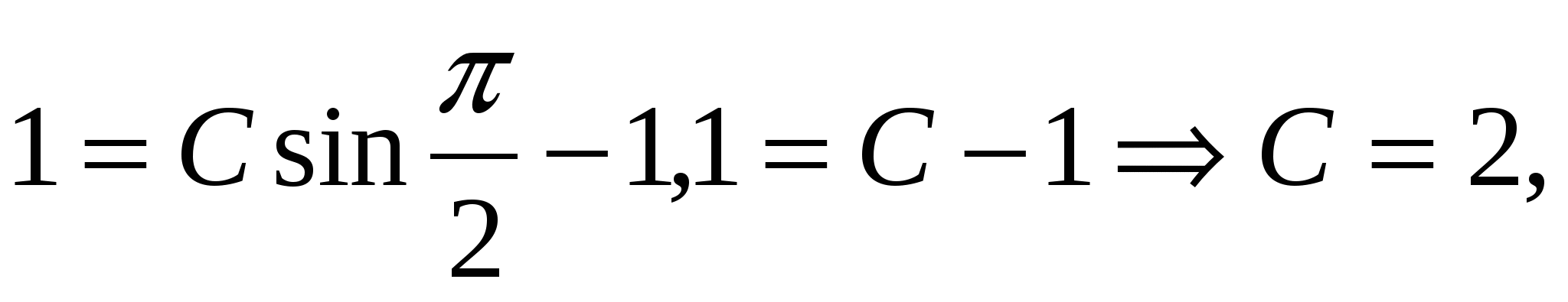 тогда у=2sinx-1- частное решение.
тогда у=2sinx-1- частное решение.
Дополнительно:
1. 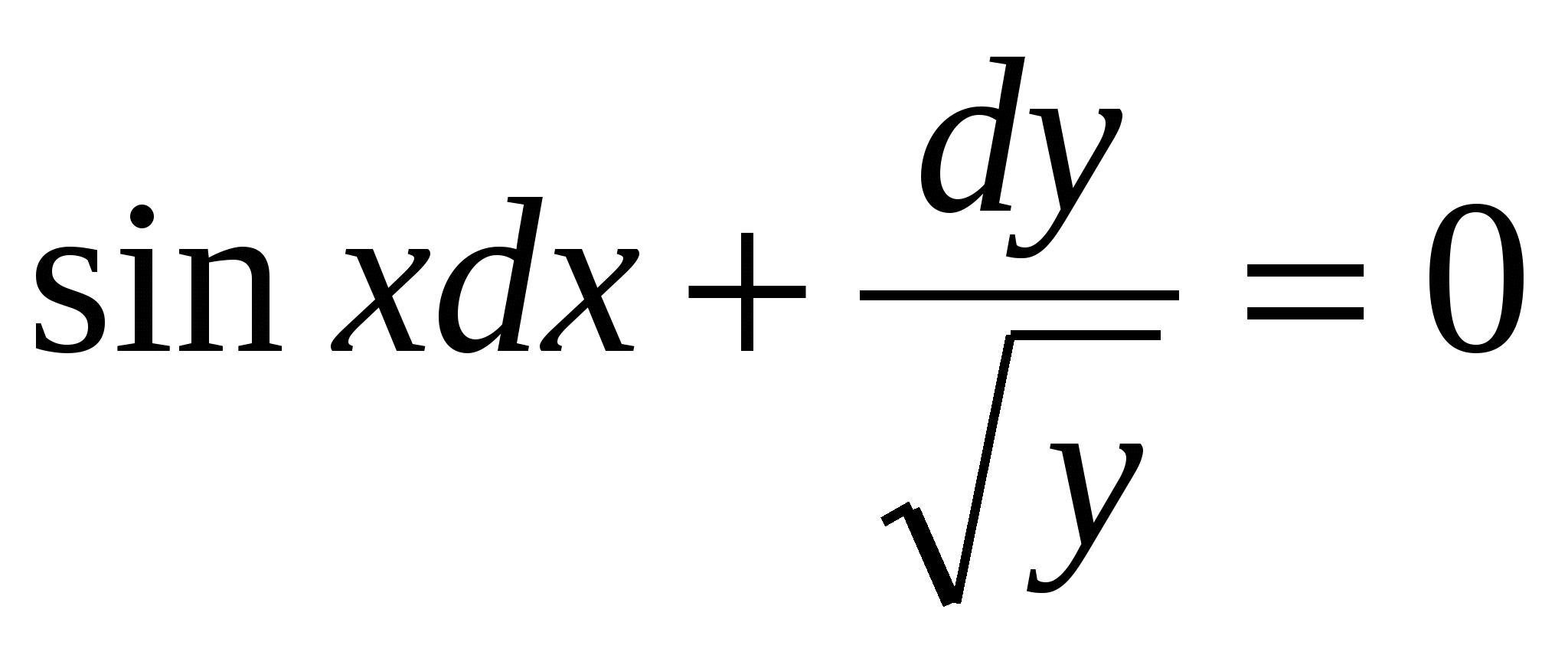 , при х=π, у=0. Ответ:
, при х=π, у=0. Ответ: 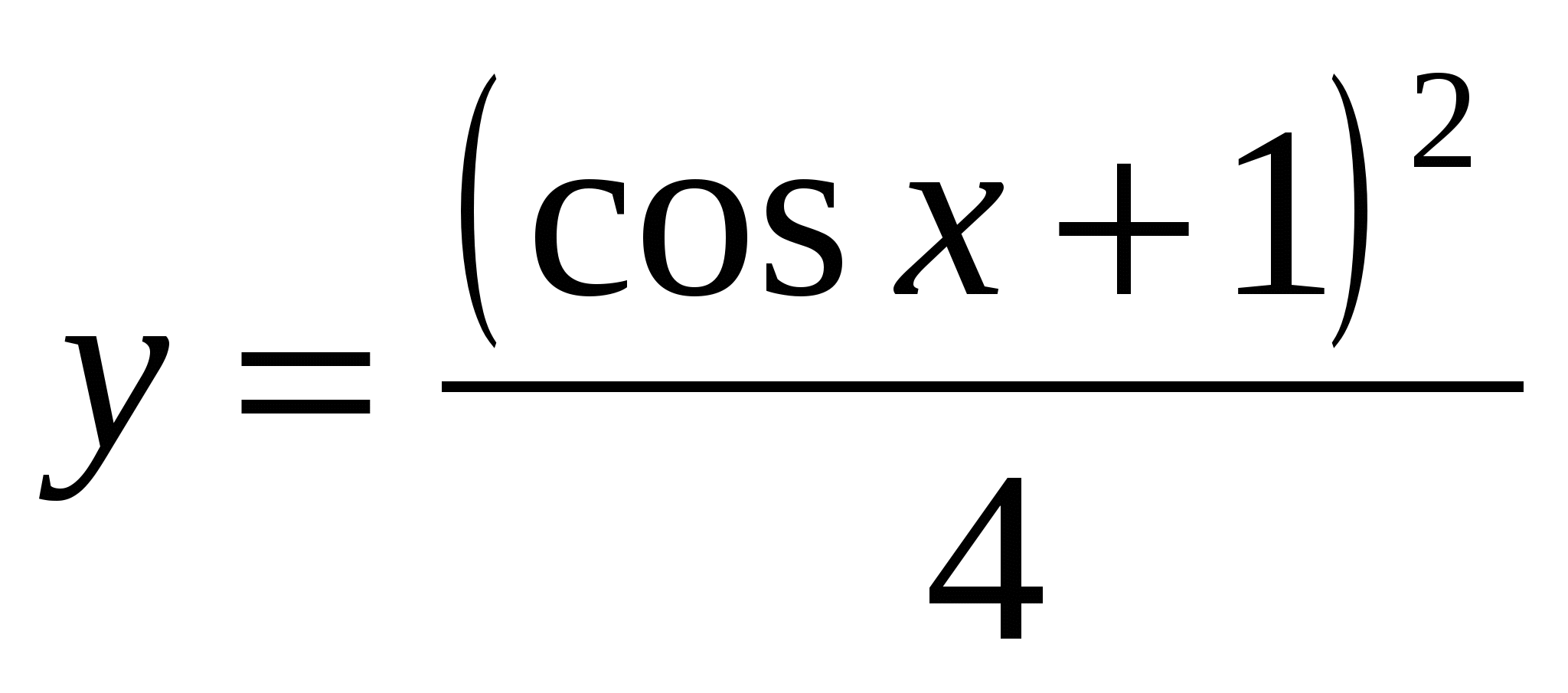
2. 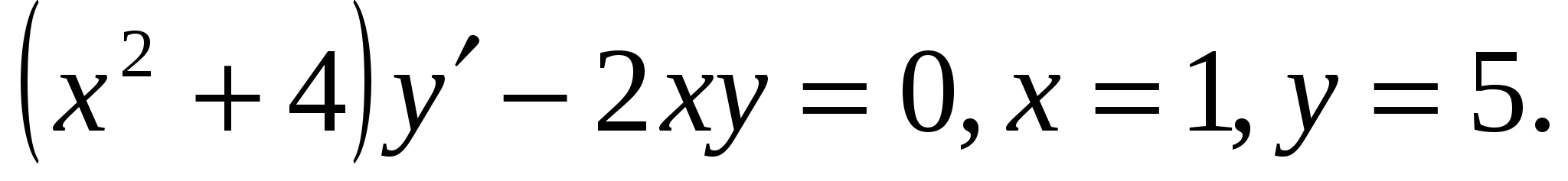 Ответ: у=х2+4
Ответ: у=х2+4
3. 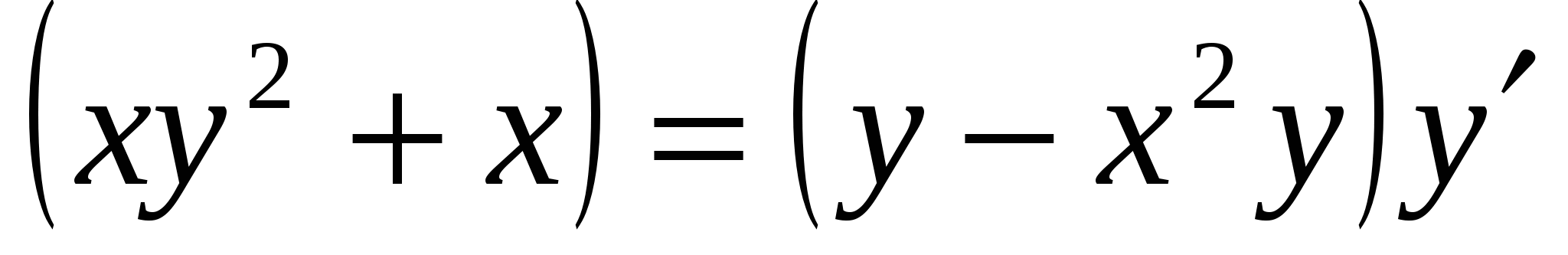 ,х=2,у=-4. ответ:
,х=2,у=-4. ответ: