Ряды с членами произвольного знака

Числовые ряды

Пусть дана числовая последовательность { u_n }, n =1,2,… u_n R. Выражение вида
u ₁+ u ₂+…+ u_n +…называют числовым рядом и обозначают

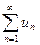, (1)

Числа u ₁, u ₂,…, u_n называют членами ряда (1), а u_n = f (n) – общим членом ряда (1).

Сумма n первых членов ряда S_n = u ₁+ u ₂+…+ u_n называется n -ой частичной суммой ряда (1).

Числовой ряд (1) называют сходящимся, если существует конечный предел последовательности его n -ых частичных сумм

(2)

Этот предел называют суммой ряда (1). Если конечный предел (2) не существует, то ряд (1) называют расходящимся.

Сходящиеся числовые ряды обладают следующими свойствами.

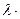1. Если ряд (1) сходится и имеет сумму S, то сходится и ряд вида , и имеет сумму S.

2. Если ряды 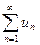и сходятся и имеют суммы соответственно S ₁ и S ₂, то сходится и ряд 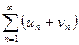и имеет сумму S ₁+ S ₂.

3. Отбрасывание или присоединение конечного числа членов числового ряда не влияет на его сходимость или расходимость. При этом ряд , полученный отбрасыванием первых n членов ряда, называют n -ым остатком ряда, S = S_n + r_n.

4. Для того, чтобы ряд (1) сходился, необходимо и достаточно, чтобы при 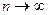остаток ряда стремился к нулю, т.е. .

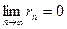Необходимое условие сходимости числового ряда определяет теорема: если ряд (1) является сходящимся, то предел его общего члена u_n при 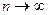равен нулю, т.е. 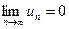. Обратное, вообще говоря, неверно.

Следствие. Если предел общего члена числового ряда (1) при 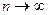не равен нулю, то ряд расходится.

Знакоположительные ряды

Числовой ряд (1) называют положительным, если для всех номеров n u_n >0.

Критерий сходимости положительных числовых рядов определяет теорема: положительный числовой ряд сходиться тогда и только тогда, когда последовательность его n -ых частичных сумм ограничена сверху.

Для исследования сходимости знакоположительных числовых рядов на практике применяют не критерий, а признаки их сходимости.

1 Признак сравнения

Пусть даны два положительных ряда 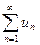и , удовлетворяющих условию для любого n =1,2,… Тогда из сходимости ряда следует сходимость ряда 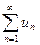, а из расходимости ряда 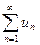следует расходимость ряда . При этом в качестве «эталонных» рядов часто используют следующие ряды:

- геометрический ряд 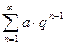, сходящийся при | q |<1 и расходящийся в противном случае;

- гармонический ряд 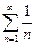– расходящийся;

- обобщенный гармонический ряд 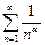– сходящийся при 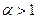и расходящийся при .

2 Предельный признак сравнения

Если для положительных рядов 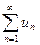и существует и конечен предел отношения их общих членов 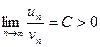, то эти ряды ведут себя одинаково.

3 Предельный признак Даламбера

Пусть для знакоположительного ряда 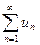существует предел отношения его n -го и (n +1)-го членов . Тогда при l <1 ряд сходится, при l >1 расходится, а случай l =1 является сомнительным и требует использования другого признака сходимости.

4 Предельный признак Коши

Пусть для знакоположительного ряда 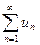существует предел 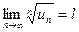. Тогда при l <1 ряд сходится, при l >1 расходится, а случай l =1 является сомнительным и требует использования другого признака сходимости.

Замечание Признак Коши является более чувствительным, чем признак Даламбера, т.к. если к ряду применим признак Даламбера, то к нему применим и признак Коши. Обратное неверно.

5 Интегральный признак сходимости

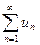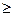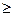Пусть дан знакоположительный ряд с невозрастающими членами u ₁ u ₂ … u_n 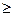…, и функция y = f (x), определенная, непрерывная и невозрастающая при x 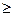1, причем f (1)= u ₁,
f (2)= u ₂,…, f (n)= u_n,,… Тогда для сходимости ряда 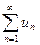необходимо и достаточно сходимости несобственного интеграла .

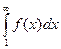Ряды с членами произвольного знака

Числовой ряд (1) 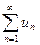называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов

. (3)

Числовой ряд (1) называется условно сходящимся, если числовой ряд 91) сходится, а числовой ряд (3) расходится.

Справедлива теорема: если ряд (1) сходится абсолютно, то он и просто сходится, т.е. из сходимости ряда (3) следует сходимость ряда (1).

Применение к сходящемуся ряду (3) признаков сходимости знакоположительных рядов позволяет установить сходимость ряда (1). При этом если ряд (3) расходится, то это не означает в общем случае расходимость ряда (1). Однако, если ряд (3) расходится по признакам Даламбера или Коши, то это означает, что нарушается необходимое условие сходимости числового ряда (1), т.е. , а значит, ряд (1) расходится.

Абсолютно и условно сходящиеся ряды обладают следующими свойствами.

1 Пусть , k =1,2,… – произвольная подпоследовательность последовательности 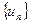, n =1,2,… Тогда из сходимости ряда 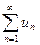следует сходимость ряда .

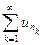2 Если числовой ряд (1) сходится условно, то ряды, составленные из его положительных и отрицательных членов, расходятся.

3 Сочетательное свойство рядов. Пусть ряд (1) сходится, тогда ряд, полученный группировкой его членов без изменения их порядка также сходится, причем его сумма совпадает с суммой исходного ряда.

4 Переместительное свойство (теорема Дирихле) для абсолютно сходящихся рядов. Если ряд (1) абсолютно сходится, то сходится и ряд, полученный перестановкой его членов, причем его сумма совпадает с суммой исходного ряда.

5 Теорема Римана для условно сходящихся рядов. Если числовой ряд (1) сходится условно, то перестановкой его членов можно получить

1) ряд, сходящийся к любому заданному числу;

2) расходящийся ряд;

3) колеблющийся ряд, т.е. ряд, сумма которого не существует.

Признаки сходимости произвольных числовых рядов целесообразно использовать для рядов, которые не являются абсолютно сходящимися. Их применяют к числовым рядам вида

, (4)

где { u_n } и { v_n }, n =1,2,… – числовые последовательности.

Последовательность { v_n }, n =1,2,… называют последовательностью с ограниченным изменением, если сходится ряд .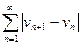

1 Первый признак Абеля. Если последовательность n -ых частичных сумм ряда 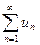ограничена, а последовательность { v_n }, n =1,2,… – последовательность с ограниченным изменением, то ряд (4) сходится.

2 Второй признак Абеля. Если числовой ряд 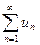сходится, и последовательность { v_n }, n =1,2,… – последовательность с ограниченным изменением, то ряд (4) сходится.

3 Признак Дирихле-Абеля. Если последовательность n -ых частичных сумм ряда 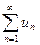ограничена, последовательность { v_n }, n =1,2,… является невозрастающей и , то ряд (4) сходится.

Числовой ряд (1) называют знакочередующимся, если любые два его соседних члена имеют противоположные знаки, т.е.

, u_n >0. (5)

4 Признак Лейбница сходимости знакочередующихся рядов. Если члены знакочередующегося ряда (5) по модулю монотонно убывая стремятся к нулю, то ряд (5) сходится.

Функциональные ряды

Если для некоторого фиксированного множества X каждому натуральному числу n ставится в соответствие по определенному закону некоторая функция f_n (x), заданная на множестве X, то последовательность функций f ₁(x), f ₂(x), …, f_n (x),… называют функциональной последовательностью. Функция 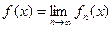называется предельной функцией функциональной последовательности { f_n (x)}, n =1,2,… Отдельные функции f ₁(x), f ₂(x), …, f_n (x),… называют членами или элементами функциональной последовательности, а множество X – ее областью определения.

Функциональным рядом называется выражение вида

u ₁(x)+ u ₂(x)+…+ u_n (x)+…= (1),

где { u_n (x)}, n =1,2,… – функциональная последовательность. Здесь u_n (x) – общий или n -ый член функционального ряда, множество X, на котором определены его члены, называют областью определения функционального ряда. В каждой конкретной точке области определения x ₀ X функциональный ряд (1) представляет собой числовой ряд.

Сумма n первых членов функционального ряда (1)

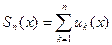(2)

называется его n -ой частичной суммой.

Функциональный ряд (1) называется сходящимся в точке x ₀ X, если существует конечный предел последовательности его n -ых частичных сумм в этой точке, т.е. .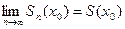

Областью сходимости функционального ряда (1) называется множество всех тех значений из области определения x X, при которых ряд (1) сходится. Суммой функционального ряда (1) будет функция 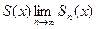для всех x X.