Равномерная сходимость функционального ряда

Говорят, что функциональная последовательность { f_n ( x )}, n =1,2,… сходится к функции f ( x ) равномерно на множестве X, если для любого сколь угодно малого положительного числа найдется номер члена последовательности, зависящий от 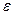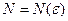, что для всех элементов последовательности с номерами и всех значений из области определения функциональной последовательности x X будет выполняться неравенство 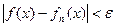. Равномерная сходимость обозначается как f_n 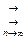(x) f (x)

Замечание В определении равномерной сходимости важно, что номер не зависит от x X. Кроме того, из сходимости функциональной последовательности на множестве X не следует ее равномерная сходимость на этом множестве.

Функциональный ряд (1) называется равномерно сходящимся на множестве X к своей сумме S (x), если последовательность его n -ых частичных сумм { S_n (x)}, n =1,2,…сходится равномерно на этом множестве к предельной функции S (x).

Критерий Коши равномерной сходимости функционального ряда формулируется следующим образом: для того чтобы функциональный ряд (1) сходился равномерно на множестве X необходимо и достаточно, чтобы для любого сколь угодно малого положительного числа нашелся такой номер члена ряда, зависящий от 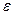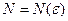, что для всех членов ряда с номерами 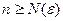, всех натуральных чисел 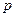и всех значений x X выполнялось неравенство .

Для исследования сходимости функциональных рядов на практике используют признаки их сходимости.

Говорят, что функциональная последовательность { f_n (x)}, n =1,2,… равномерно ограничена на множестве X, если существует такое действительное число A, что для всех номеров n и всех значений x 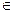X справедливо неравенство | f_n (x)|< A.

1 Признак Дирихле-Абеля. Функциональный ряд равномерно сходится на множестве X, если функциональная последовательность { v_n (x)}, n =1,2,… является невозрастающей на этом множестве и равномерно сходится к нулю, т.е. v ₁(x) ≥v ₂(x) ≥ … ≥v_n (x) ≥ … и v_n (x) 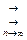0, а ряд имеет равномерно ограниченную на X последовательность n -ых частичных сумм.

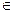2 Признак Вейерштрасса. Если функциональный ряд (1) определен на множестве X, и существует сходящийся числовой ряд такой, что для всех x X и любого номера n справедливо неравенство | u_n (x)|≤ c_n, то функциональный ряд (1) равномерно сходится на X. Иначе: функциональный ряд (1) равномерно сходится на множестве X, если его можно мажорировать на этом множестве сходящимся числовым рядом.

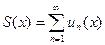3 Признак Дини. Если члены u_n (x) сходящегося на множестве X функционального ряда (1) непрерывны на этом множестве и монотонно не возрастают или не убывают в каждой точке x X, а его сумма непрерывна на множестве X, то функциональный ряд (1) равномерно сходится на X.

Равномерно сходящиеся функциональные ряды обладают следующими свойствами.

1 Достаточное условие непрерывности суммы функционального ряда. Если члены функционального ряда (1) u_n (x) со всеми номерами непрерывны в точке x ₀ 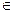X и функциональный ряд (1) равномерно сходится на X, то его сумма непрерывна в точке x ₀.

2 Предельный переход под знаком функционального ряда. Пусть функциональный ряд (1) равномерно сходится на множестве X к сумме S (x), и существует конечный предел в точке a X для любого его члена u_n (x), равный b_n, т.е. 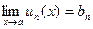. Тогда справедливо следующее соотношение: .

3 Интегрирование суммы функционального ряда. Если члены функционального ряда (1) непрерывны на отрезке [ a; b ], а сам ряд сходится равномерно на [ a; b ], то сумма (1) есть непрерывная функция, и .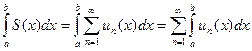

4 Дифференцирование функционального ряда. Если члены функционального ряда (1) непрерывны и дифференцируемы на множестве X, сам ряд (1) сходится на этом множестве, а ряд, составленный их производных его членов равномерно сходится на X, то сумма (1) есть дифференцируемая функция на X, и .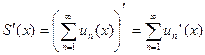

Степенные ряды

Функциональный ряд вида

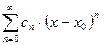() (3)

с общим членом u_n = c_n · xⁿ (u_n = c_n ·(x –x ₀ )ⁿ) называют степенным рядом.

Множество значений x, при которых ряд (3) сходится, называют областью сходимости степенного ряда.

Структура области сходимости степенного ряда (3) устанавливается теоремой Абеля. Если степенной ряд (3) сходится в точке x = a, то он сходится, и притом абсолютно, во всех точках x, удовлетворяющих условию | x |<| a |. Если степенной ряд (3) расходится в точке x = b, то он расходится во всех точках x, удовлетворяющих условию | x |>| b |.

Таким образом, областью сходимости степенного ряда (3) может быть единственная точка x =0, интервал (–| a |; | a |) или вся числовая прямая (–∞; +∞).

Для определения границ интервала сходимости используется теорема Коши-Адамара. Если областью сходимости степенного ряда (3) является промежуток, отличный от (–∞; +∞), то существует действительное число R такое, что для любого действительного числа x, удовлетворяющего неравенству | x |< R ряд (3) сходится, а для любого действительного числа x, удовлетворяющего неравенству | x |> R ряд (3) расходится. Число R называется радиусом сходимости степенного ряда (3).

Радиус сходимости степенного ряда может быть найден по признаку Даламбера как 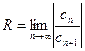либо по признаку Коши как 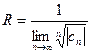. Интервал (– R; + R) называется интервалом сходимости степенного ряда (3). На концах интервала сходимости ряд (3) может быть как сходящимся, так и расходящимся.

Замечание Для степенного ряда 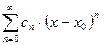интервал сходимости имеет вид (– R + х ₀; + R + х ₀).

Степенные ряды обладают следующими свойствами.

1 Равномерная сходимость степенного ряда. Пусть r Î(0; R), где R – радиус сходимости степенного ряда (3). Тогда этот ряд равномерно сходится на отрезке [– r; r ].

2 Непрерывность суммы степенного ряда. На любом отрезке [ a; b ] из интервала сходимости степенного ряда (– R; + R) его сумма есть функция непрерывная.

3 Интегрируемость суммы степенного ряда. На любом отрезке [ a; b ], содержащемся в интервале сходимости степенного ряда (– R; + R), его сумма есть функция интегрируемая, причем .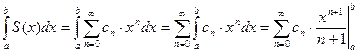

4 Дифференцируемость суммы степенного ряда. Сумма степенного ряда (3) есть функция, дифференцируемая в каждой точке области сходимости, причем .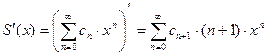

5 Неизменность радиуса сходимости при интегрировании и дифференцировании. Радиус сходимости степенного ряда (3) не меняется при почленном дифференцировании и интегрировании и совпадает с радиусом сходимости исходного ряда.