Матрицы и определители
М а т р и ц ы
Определение 2.1. Матрицей размера m  n над полем Р называется прямоугольная таблица, состоящая из m строк и n столбцов, следующего вида:
n над полем Р называется прямоугольная таблица, состоящая из m строк и n столбцов, следующего вида:
 , где aij
, где aij  P, i =
P, i =  , j =
, j =  .
.
Матрицы также можно обозначать следующим образом:
А =(aij), i=  , j=
, j=  , или
, или
А =|| aij ||, i=  , j=
, j=  .
.
Определение 2.2. Квадратной матрицей n-го порядка над полем P называется матрица размера n  n над полем P.
n над полем P.
Пусть A – квадратная матрица n -го порядка над полем P. Тогда в матрице А выделяют две диагонали: главную и побочную:



главная побочная
Строки матрицы А называют вектор-строками и обозначают следующим образом:
Аi – i -я вектор-строка матрицы А, т.е. Аi =(ai1, ai1, …,ain) = 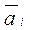 .
.
Столбцы матрицы А называют вектор-столбцами и обозначают следующим образом:
Аj – j -й вектор-столбец матрицы А, т.е. Аj =  =
=  .
. 
Определение 2.3. Две матрицы А и В размера m  n над полем P называются равными и обозначаются А=В, если в А и В элементы, стоящие на соответствующих местах, равны, т.е. aij=bij, i=
n над полем P называются равными и обозначаются А=В, если в А и В элементы, стоящие на соответствующих местах, равны, т.е. aij=bij, i=  , j=
, j=  .
.
Определение 2.4. Матрица над полем P называется нулевой и обозначается θ, если все ее элементы равны нулю, т.е.  =
=  .
.
Определение 2.5. Матрица n -го порядка над полем P называется единичной и обозначается En, если в ней на главной диагонали находятся единицы, а на остальных местах – нули, т.е.
En =  .
.
 Операции над матрицами
Операции над матрицами
1) Сложение матриц.
Определение 2.6. Пусть A =(aij), B =(bij) - матрицы размера m  n над полем Р. Матрица С=(cij) размера m
n над полем Р. Матрица С=(cij) размера m  n над полем Р называется суммой матриц А и В и обозначается С=А+В, если cij=aij+bij, i =
n над полем Р называется суммой матриц А и В и обозначается С=А+В, если cij=aij+bij, i =  , j =
, j =  .
.
Другими словами, сложение матриц одинакового размера сводится к сложению их элементов, стоящих на соответствующих местах.
2) Умножение матрицы на скаляр.
Определение 2.7. Пусть A =(aij) – матрица размера m  n над полем P,
n над полем P,  P. Матрица С =(сij) размера m
P. Матрица С =(сij) размера m  n над полем P называется произведением матрицы А на элемент
n над полем P называется произведением матрицы А на элемент  и обозначается С=
и обозначается С=  .А, если сij=
.А, если сij=  .aij, j=
.aij, j=  , i=
, i=  .
.
Другими словами, чтобы умножить матрицу А над полем Р на элемент α∈Р, необходимо каждый элемент матрицы А умножить на α.
3) Умножение матриц.
Определение 2.8. Пусть A =(aij) – матрица размера m  n над полем P, B =(bij) - матрица размера n
n над полем P, B =(bij) - матрица размера n  k над полем P. Матрица С =(сij) размера m
k над полем P. Матрица С =(сij) размера m  k над полем P называется произведением матриц А и В и обозначается С=A∙B, если элемент сij равен скалярному произведению i- й вектор-строки матрицы А на j -й вектор-столбец матрицы B, т.е.
k над полем P называется произведением матриц А и В и обозначается С=A∙B, если элемент сij равен скалярному произведению i- й вектор-строки матрицы А на j -й вектор-столбец матрицы B, т.е.
сij=Ai∙B j =(ai1,...,ain)∙  = ai1b1j+…+ainbnj =
= ai1b1j+…+ainbnj =  , i=
, i=  , j=
, j=  .
.
4) Транспонирование матрицы.
Определение 2.9. Пусть A - матрица размера m  n над полем P. Транспонированием матрицы А называется операция замены в матрице А i -й строки на i -й столбец, i=
n над полем P. Транспонированием матрицы А называется операция замены в матрице А i -й строки на i -й столбец, i=  . Матрица, полученная в результате транспонирования матрицы A, называется матрицей, транспонированной к матрице A, и обозначается tA.
. Матрица, полученная в результате транспонирования матрицы A, называется матрицей, транспонированной к матрице A, и обозначается tA.
Обратимые матрицы. Матричные уравнения.
Определение 2.10. Матрица А n -го порядка над полем Р называется обратимой, если существует такая матрица В над полем Р, что АВ=ВА=Еn. Матрица В называется матрицей, обратной для матрицы А, и обозначается А-1.
Простейшие матричные уравнения имеют вид:
1) A∙X=B, 2) X∙A=B, 3) A∙X∙B=C, где А, В, С – некоторые матрицы.
Если матрица А-1 существует, то
в случае 1): X=A-1 ∙B,
в случае 2): X=B∙A-1,
в случае 3): X∙B=A-1 ∙C.
При этом, если матрица B-1 существует, то в случае 3) X=A-1 ∙C∙B-1.
П е р е с т а н о в к и n - й с т е п е н и
Определение 2.11. Пусть М= { 1,2,…,n }. Перестановкой на множестве М или перестановкой n-й степени называется множество М с заданным расположением его элементов, и обозначается I=(i1i2…in), где i1,i2,..,in – попарно различные элементы из М.
Например, пусть М= { 1,2,3 }. Тогда перестановки на М имеют вид: I1=(132), I2=(231), I3=(123) и т.д.
Определение 2.12. Инверсией или беспорядком перестановки I называется любая пара символов перестановки I, в которой символ, стоящий левее, больше символа, стоящего правее.
Например, в перестановке I2=(231) две инверсии: 31 и 21.
Через  (I) обозначается число всех инверсий перестановки I.
(I) обозначается число всех инверсий перестановки I.
Пример 2.1. Пусть I=(312465). Тогда перестановка I имеет три инверсии 31, 32, 65, т.е.  (I)=3.
(I)=3.
Определение 2.13. Перестановка I называется чётной, если  (I) – чётное число, в противном случае перестановка I называется нечётной.
(I) – чётное число, в противном случае перестановка I называется нечётной.
В примере 2.1 перестановка I – нечётная.
Через Sn обозначается множество всех перестановок n -ой степени.
Утверждение 2.1. | Sn |=n!.
О п р е д е л и т е л и
Пусть А = 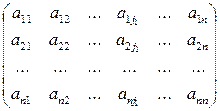 - матрица n -го порядка над полем Р.
- матрица n -го порядка над полем Р.
Из элементов матрицы А будем составлять всевозможные произведения, состоящие из n множителей, любые два различных из которых находятся в разных строках и разных столбцах. Таким, например, является произведение элементов, стоящих на главной диагонали: a11a22…ann. Все такие произведения можно получить по следующему правилу: выберем для произведения из первой строки матрицы А некоторый элемент  , затем вычеркнем первую строку и j1 -й столбец, и в полученной подматрице из первой строки выбираем некоторый элемент
, затем вычеркнем первую строку и j1 -й столбец, и в полученной подматрице из первой строки выбираем некоторый элемент  и т.д. Через конечное число шагов получим произведение вида:
и т.д. Через конечное число шагов получим произведение вида: 
 …
…  .
.
Так как j1,j2,…,jn – попарно различные элементы из множества М= { 1,2,…,n }, то вторые индексы в записанном произведении образуют перестановку I=(j1j2…jn).
Рассмотрим выражение вида: (-1)  (I)∙
(I)∙ 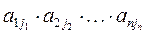 (1), где I=(j1j2…jn).
(1), где I=(j1j2…jn).
Выражений вида (1) можно образовать столько, сколько существует перестановок, составленных из вторых индексов, т.е., ввиду утверждения 2.1, их будет n!.
Определение 2.14. Пусть А =  - матрица n- го порядка над полем Р. Определителем матрицы А (или, коротко, определителем n-го порядка) называется элемент поля Р, равный
- матрица n- го порядка над полем Р. Определителем матрицы А (или, коротко, определителем n-го порядка) называется элемент поля Р, равный
 .
.
Для определителя n- го порядка используются следующие обозначения: 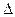 =
=  ,
,  =| A |,
=| A |,  =| aij |, i =
=| aij |, i =  , j =
, j =  ,
,  = detA (
= detA ( - читается «дельта »).
- читается «дельта »).
1) Пусть Δ – определитель 2-го порядка, т.е.
Δ = 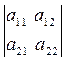 =
=  .
.
Отметим, что  = 2! = 2; M =
= 2! = 2; M = 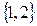 .
.
Так как I 1 = (12), то 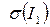 = 0
= 0 
 ,
,
I 2 = (21), то  = 1
= 1 
 , и значит,
, и значит,
Δ = 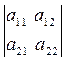 =
=  .
.
Таким образом, определитель 2-го порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.
2) Пусть Δ - определитель 3-го порядка:
Δ = 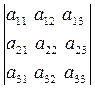 =
=  .
.
Отметим, что | S 3|= 3! = 6; M =  . Тогда
. Тогда
I 1 = (123)  = 0
= 0  ;
;
I 2 = (213)  = 1
= 1  ;
;
I 3 = (312)  = 2
= 2  ;
;
I 4 = (321)  = 3
= 3  ;
;
I 5 = (132) 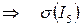 = 1
= 1  ;
;
I 6 = (231)  = 2
= 2  .
.
Следовательно,
Δ=  =
= 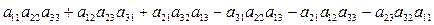 .
.
Таким образом, определитель 3-го порядка равен сумме шести слагаемых, три из которых со знаком +:
- произведение элементов на главной диагонали,
- произведение элементов на диагонали, параллельной главной, умноженное на элемент, стоящий в противоположном углу,
- произведение элементов второй диагонали, параллельной главной, умноженное на элемент, стоящий в противоположном углу;
Остальные три слагаемых получают аналогично, только рассуждения проводят для побочной диагонали.
Записанное правило называют правилом Саррюса.
Определение 2.15. Пусть Δ = 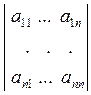 . Если в определителе Δ сгруппировать все слагаемые, содержащие элемент
. Если в определителе Δ сгруппировать все слагаемые, содержащие элемент  , и сгруппировав, вынести элемент
, и сгруппировав, вынести элемент  за скобки, то выражение, полученное в скобках, обозначается Aij и называется алгебраическим дополнением к элементу
за скобки, то выражение, полученное в скобках, обозначается Aij и называется алгебраическим дополнением к элементу  в определителе Δ, i =
в определителе Δ, i =  , j =
, j =  .
.






 Так как все элементы i -той строки определителя Δ входят в одно и только одно из слагаемых, то Δ= ai1Ai1+ ai2Ai2+ … + ainAin (1).
Так как все элементы i -той строки определителя Δ входят в одно и только одно из слагаемых, то Δ= ai1Ai1+ ai2Ai2+ … + ainAin (1).
Равенство (1) называется разложением определителя Δ по i-той строке.
 Аналогично: Δ= a1jA1j+ a2jA2j+ … + anjAnj (2) - разложение определителя Δ по j-тому столбцу, j =
Аналогично: Δ= a1jA1j+ a2jA2j+ … + anjAnj (2) - разложение определителя Δ по j-тому столбцу, j =  .
.
Строки и столбцы определителя Δ называются его рядами. Таким образом, (1) и (2) – разложения Δ по ряду.
Определение 2.16. Если в определителе Δ = 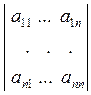 вычеркнуть i -тую строку и j -тый столбец, то на их пересечении получится элемент aij, а остальные элементы образуют определитель (n-1) -го порядка, который обозначается Mij и называется минором к элементу aij в определителе Δ, i =
вычеркнуть i -тую строку и j -тый столбец, то на их пересечении получится элемент aij, а остальные элементы образуют определитель (n-1) -го порядка, который обозначается Mij и называется минором к элементу aij в определителе Δ, i =  , j =
, j =  .
.
Например:
Пусть Δ =  . Тогда, например, M23 =
. Тогда, например, M23 =  .
.


 Теорема 2.1. Пусть Δ - определитель n-го порядка над полем P, Aij и Mij – алгебраическое дополнение и минор к элементу aij в Δ соответственно. Тогда
Теорема 2.1. Пусть Δ - определитель n-го порядка над полем P, Aij и Mij – алгебраическое дополнение и минор к элементу aij в Δ соответственно. Тогда
Aij=(-1)i+ j ∙Mij, i =  , j =
, j =  .
.
 |
Теорема 2.2. Квадратная матрица А является обратимой тогда и только тогда, когда |A| ≠ 0.
Теорема 2.3. Пусть A=  - матрица n-го порядка над полем P,
- матрица n-го порядка над полем P,  =
= 
 0. Тогда
0. Тогда
А  =
= 
 ∙
∙ 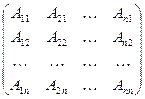 ,
,
где Аij - алгебраическое дополнение к элементу аij в матрице А, i=  , j=
, j=  .
.
Системы линейных алгебраических уравнений
Определение 2.17. Система линейных уравнений вида
(1)  , где
, где 

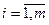
 ,
,  поле, называется системой m линейных уравнений с n неизвестными
поле, называется системой m линейных уравнений с n неизвестными  над полем Р,
над полем Р,  - коэффициенты при неизвестных,
- коэффициенты при неизвестных,  - свободные члены системы (1),
- свободные члены системы (1), 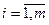 ,
,  .
.
Определение 2.18. Упорядоченная n -ка (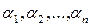 ), где
), где 
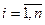 , называется решением системы линейных уравнений (1), если при замене переменной
, называется решением системы линейных уравнений (1), если при замене переменной  на
на  каждое уравнение системы (1) превращается в верное числовое равенство.
каждое уравнение системы (1) превращается в верное числовое равенство.
Определение 2.19. Система линейных уравнений (1) называется совместной, если она имеет хотя бы одно решение. В противном случае система (1) называется несовместной.
Определение 2.20. Система линейных уравнений (1) называется определенной, если она имеет единственное решение. В противном случае система (1) называется неопределенной.
Определение 2.21. Система линейных уравнений над полем Р называется однородной, если все ее свободные члены равны нулю. В противном случае система называется неоднородной.
Однородная система линейных уравнений всегда совместна, так как всегда имеет решение  .
.
Однородная система вида  называется однородной системой, ассоциированной с системой (1).
называется однородной системой, ассоциированной с системой (1).
Для каждой системы линейных уравнений можно ввести в рассмотрение две матрицы - основную и расширенную.
Определение 2.22. Основной матрицей системы линейных уравнений (1) называется матрица, составленная из коэффициентов при неизвестных, т.е. матрица следующего вида:  .
.
Определение 2.23. Расширенной матрицей системы линейных уравнений (1) называется матрица  , полученная из матрицы
, полученная из матрицы  путем присоединения к ней столбца свободных членов:
путем присоединения к ней столбца свободных членов:
 .
.
Определение 2.24. Элементарными преобразованиями системы линейных уравнений называются следующие:
1) умножение обеих частей некоторого уравнения системы на элемент  ;
;
2) прибавление к обеим частям одного уравнения системы соответствующих частей другого уравнения, умноженных на элемент  ;
;
3) добавление или отбрасывание уравнения вида  .
.
Определение 2.25. Элементарными преобразованиями матрицы называются следующие:
1) умножение всех элементов некоторой строки матрицы на элемент  ;
;
2) прибавление к элементам некоторой строки матрицы соответствующих элементов другой строки, умноженных на  ;
;
3) добавление или отбрасывание нулевой строки.
Определение 2.26. Две системы линейных уравнений над полем Р относительно переменных  называются равносильными, если их множества решений совпадают.
называются равносильными, если их множества решений совпадают.
Теорема 2.4. Если одна система линейных уравнений получена из другой с помощью элементарных преобразований, то такие системы равносильны.
Теорема 2.5 (правило Крамера).
Пусть (1)  - система n линейных уравнений с n неизвестными над полем P, А=
- система n линейных уравнений с n неизвестными над полем P, А=  - основная матрица системы (1),
- основная матрица системы (1),  =
=  . Если
. Если  , то система (1) имеет единственное решение:
, то система (1) имеет единственное решение:  ,
,  , …,
, …,  ,
,
где  - определитель, полученный из
- определитель, полученный из  заменой i-го столбца на столбец свободных членов, i=
заменой i-го столбца на столбец свободных членов, i=  , т.е.
, т.е.
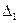 =
=  , …,
, …, 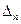 =
=  .
.
Теорема 2.6 (теорема Кронекера-Капелли).
Пусть (1)  - неоднородная система линейных уравнений над полем P, A и
- неоднородная система линейных уравнений над полем P, A и  - соответственно основная и расширенная матрицы системы (1). Система (1) является совместной тогда и только тогда, когда r(A)=r(
- соответственно основная и расширенная матрицы системы (1). Система (1) является совместной тогда и только тогда, когда r(A)=r(  ), причём, если r=n (где r=r(A)), то система (1) определена, а если r<n, то система (1) неопределена.
), причём, если r=n (где r=r(A)), то система (1) определена, а если r<n, то система (1) неопределена.
Замечание 2.1. Рангомматрицы A называется ранг r(A) её системы векторов-строк (см. определение 2.32). Рангматрицыравен числу ненулевых строк в матрице после приведения ее к ступенчатому виду.