1. Составить расширенную матрицу 
системы линейных уравнений (1) и с помощью элементарных преобразований привести к ступенчатому виду.
2. Провести исследование:
а) если 
, то система (1) несовместна;
б) если 
, то система (1) совместна. При этом,
если r=n, то система (1) определена,
если r<n, то система (1) неопределена.
3. Найти решение системы уравнений, которая соответствует полученной ступенчатой матрице.
Задание 1. Вычислить А+В, А-В, n∙А, tB, А∙В, В∙А:
, 
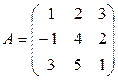, n =5.
Решение:
Пусть 
, 
. Тогда,
ввиду определений 2.6 и 2.7 (см. стр.35): 
;
; 
. По определению 2.9, 
. Согласно определению 2.8, 
∙ 
=
= 
;
=
= 
.
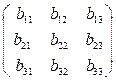Таким образом, получаем
,
,
, 
,
∙ 
=
= 
,
=
= 
.
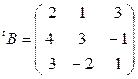Ответ: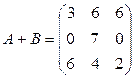 
, 
, 
,
, 
, 
.
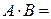
Задание 2. Вычислить определитель матрицы А из задания 1 двумя способами: а) по правилу Саррюса; б) разложением по ряду.
Решение:
а) Согласно правилу Саррюса (см. стр. 40), определитель 3-го порядка равен сумме шести слагаемых: 
• • • • • •
• • • • • •
• • • • • •
Таким образом,
б) Вычислим определитель матрицы А с помощью разложения определителя по ряду. Согласно формуле (1) (см. стр. 40), разложение определителя матрицы А по i- й строке имеет вид:
Согласно формуле (2) (стр. 40), разложение определителя матрицы А по j- му столбцу имеет вид:
Отметим, что Aij – алгебраическое дополнение к элементу аij в определителе 
(см. стр. 40, определение 2.15). По теореме 2.1 (стр. 41) Aij вычисляют по формуле Aij=(-1)i+ j ∙Mij, где Mij – минор к элементу аij в определителе 
(см. стр. 41, определение 2.16), i = 
, j = .
Вычислим определитель матрицы А, например, с помощью разложения по 3-й строке:
Отметим, что 
(см. стр. 39).
Ответ: =-43.
Задание 3. Для матрицы В из задания 1 найти обратную матрицу
В-1 двумя способами: а) с помощью элементарных преобразований;
б) с помощью алгебраических дополнений.
Решение:
Предварительно установим, является ли матрица В обратимой. Ввиду теоремы 2.2 (см. стр. 41), достаточно найти определитель матрицы В:
Так как 
, то, согласно теореме 2.2, матрица В-1 существует.
а) Вычислим матрицу В-1 с помощью элементарных преобразований. Для этого запишем расширенную матрицу вида 
и с помощью элементарных преобразований (см. стр. 43, определение 2.25) приведем подматрицу В в ней к единичной матрице En. Тогда в правой части полученной расширенной матрицы будет находиться матрица В-1:
∼ …∼ 
.
Таким образом,
∼ 
∼ 
∼
∼ 
∼
∼ 
∼ 
∼
∼ 
. Отсюда следует, что В-1 = 
, т.е.
В-1 = 
.
б) Вычислим матрицу В-1 с помощью алгебраических дополнений. Согласно теореме 2.3 (стр. 41), В 
= 
∙ 
,
где Аij - алгебраическое дополнение к элементу аij в матрице В, i= 
, j= . Таким образом, ввиду теоремы 2.1,
Тогда В-1 = 
= 
.
Ответ: В-1 = 
.
Задание 4. Решить систему линейных уравнений двумя способами: а) по правилу Крамера; б) матричным способом:
(1).
Решение:
а) Решим систему (1) по правилу Крамера (см. стр. 44, теорема 2.5). Для этого выпишем основную матрицу системы (1) (см. стр. 43, определение 2.22) и вычислим ее определитель:
; 
Согласно теореме 2.5, система (1) имеет единственное решение:
, 
, 
(2),
где 
- определитель, полученный из 
заменой i -го столбца на столбец свободных членов, i = . Найдем 
, 
, 
:
Тогда, ввиду (2), получаем 
, 
, 
.
б) Решим систему линейных уравнений (1) матричным способом. Для этого составим матричное уравнение А∙Х=В (3), где А – основная матрица системы (см. пункт а)); В – матрица, состоящая из столбца свободных членов, т.е. 
; 
. Система линейных уравнений (1) и матричное уравнение (3) являются равносильными. Действительно, А∙Х=В ⇔
∙ 
= 
⇔ 
= ⇔ 
.
Решим уравнение (3). Для этого вычислим матрицу А-1 (см. решение задания 3):
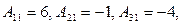
Тогда А-1 = 
, и значит,
.
Следовательно, 
, 
, 
.
Ответ: (2,-1,-3).
Задание 5. Решить систему линейных уравнений методом Гаусса:
. (1)
Решение:
Воспользуемся алгоритмом решения систем линейных уравнений методом Гаусса (см. стр. 45). Для этого составим расширенную матрицу 
системы (1) и приведем ее с помощью элементарных преобразований к ступенчатому виду:
∿
∿ 
∿
∿ 
.
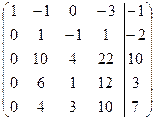Отсюда следует, что ранг расширенной матрицы системы (1) равен 3 (число ненулевых строк в матрице после приведения ее к ступенчатому виду) и равен рангу основной матрицы системы (матрицы из коэффициентов при неизвестных). Поэтому, согласно теореме Кронекера-Капелли (см. стр 44, теорема 2.6), система (1) является совместной. Так как ранг расширенной матрицы не равен числу неизвестных, то система (1) является неопределенной. Запишем систему линейных уравнений, соответствующую ступенчатой матрице:
(2) 
.
Отметим, что, согласно теореме 2.4 (см. стр. 44), системы (1) и (2) являются равносильными, т.е. множества их решений совпадают. В системе (2) неизвестные 
являются главными, а 
- свободная неизвестная. Найдем общее решение системы (2), а значит, и системы (1):
,
т.е. общее решение системы (1) имеет вид
ℝ.
Придавая 
произвольные значения, можно получить частные решения системы (1). Например, 
или 
.