Введение
Прикрепим карандаш к границе круга и прокатим его внутри другого круга, большего диаметра. Кривую, которую нарисовал карандаш, называют гипоциклоидой (рис.1).

рис.1
Актуальность выбранной темы. В литературе мы нашли чертежи нескольких гипоциклоид для случая, когда отношение диаметров большого и маленького кругов равно целому числу. Мы заинтересовались этой темой и решили с помощью собственных чертежей изучить, какие бывают гипоциклоиды.
Цель: исследовать, какие бывают гипоциклоиды в зависимости от соотношения длин большой и маленькой окружности.
Задачи:
¾ Изучить соответствующую литературу, посвященную данной проблематике;
¾ Построить графическую интерактивную модель гипоциклоиды GeoGebra
¾ Исследовать зависимость формы гипоциклоиды от отношения радиусов неподвижной и катящейся окружностей;
¾ Исследовать смыкаемость гипоциклоиды.
Объект исследования: гипоциклоиды
Предмет исследования: свойства гипоциклоиды
Актуальность: В 13 веке гипоциклоиды начал изучать математик и астроном Мухаммед Насирэддин ат-Туси (Азербайджан). Начало систематического изучения гипоциклоид было положено в 1525 г. знаменитым немецким художником Альбрехтом Дюрером. В научной литературе приводятся примеры нескольких гипоциклоид для случая, когда отношение диаметров большого и маленького кругов равно целому числу. Из чего следует, что область гипоциклоид недостаточно изучена.
Глава 1.
Для исследования мы построили интерактивную модель в программе GeoGebra. Чтобы это сделать, нам потребовалось ввести три параметра: R –радиус большой окружности, r – радиус катящейся окружности,  - градусная мера, показывающая, на сколько по большой окружности прокатилась маленькая. Задали коэффициент отношения радиусов двух окружностей k. Построили окружность с центром в точке O и радиусом R. Задали поворот точки T, фиксированной на окружности (O; R). Затем, построили вспомогательную окружность с центром в точке T и радиусом r. Нашли точку пересечения радиуса окружности (O;R) со вспомогательной окружностью – точка C. Строим окружность с центром в этой точке через уже имеющуюся точку T. Задаем точку P и ее поворот по окружности малого радиуса. Вводим параметрическое уравнение кривой
- градусная мера, показывающая, на сколько по большой окружности прокатилась маленькая. Задали коэффициент отношения радиусов двух окружностей k. Построили окружность с центром в точке O и радиусом R. Задали поворот точки T, фиксированной на окружности (O; R). Затем, построили вспомогательную окружность с центром в точке T и радиусом r. Нашли точку пересечения радиуса окружности (O;R) со вспомогательной окружностью – точка C. Строим окружность с центром в этой точке через уже имеющуюся точку T. Задаем точку P и ее поворот по окружности малого радиуса. Вводим параметрическое уравнение кривой
 .
.
Кривая образуется при движении окружности малого радиуса по внутренней области окружности большого радиуса. След оставляет точка P.
Отношение длин большой и маленькой окружности равно целому числу.
Отношение равно 4. За один оборот маленький круг прокатывается по одной четверти большого круга.
За 4 оборота маленький круг полностью прокатывается по большому кругу и точка, зафиксированная на окружности возвращается в начальное положение. Получаем гипоциклоиду следующего вида (см.рис.2). Такая гипоциклоида в математике называется астроида.

рис.2
Если же, отношение равно 3, маленький круг сделал вокруг себя три оборота, прокатился по большому кругу один раз. Полученная кривая называется дельтоидой. (рис.3)

рис.3
Также продемонстрируем кривые, полученные при k= 5, k=6. (см. рис. 4,5)
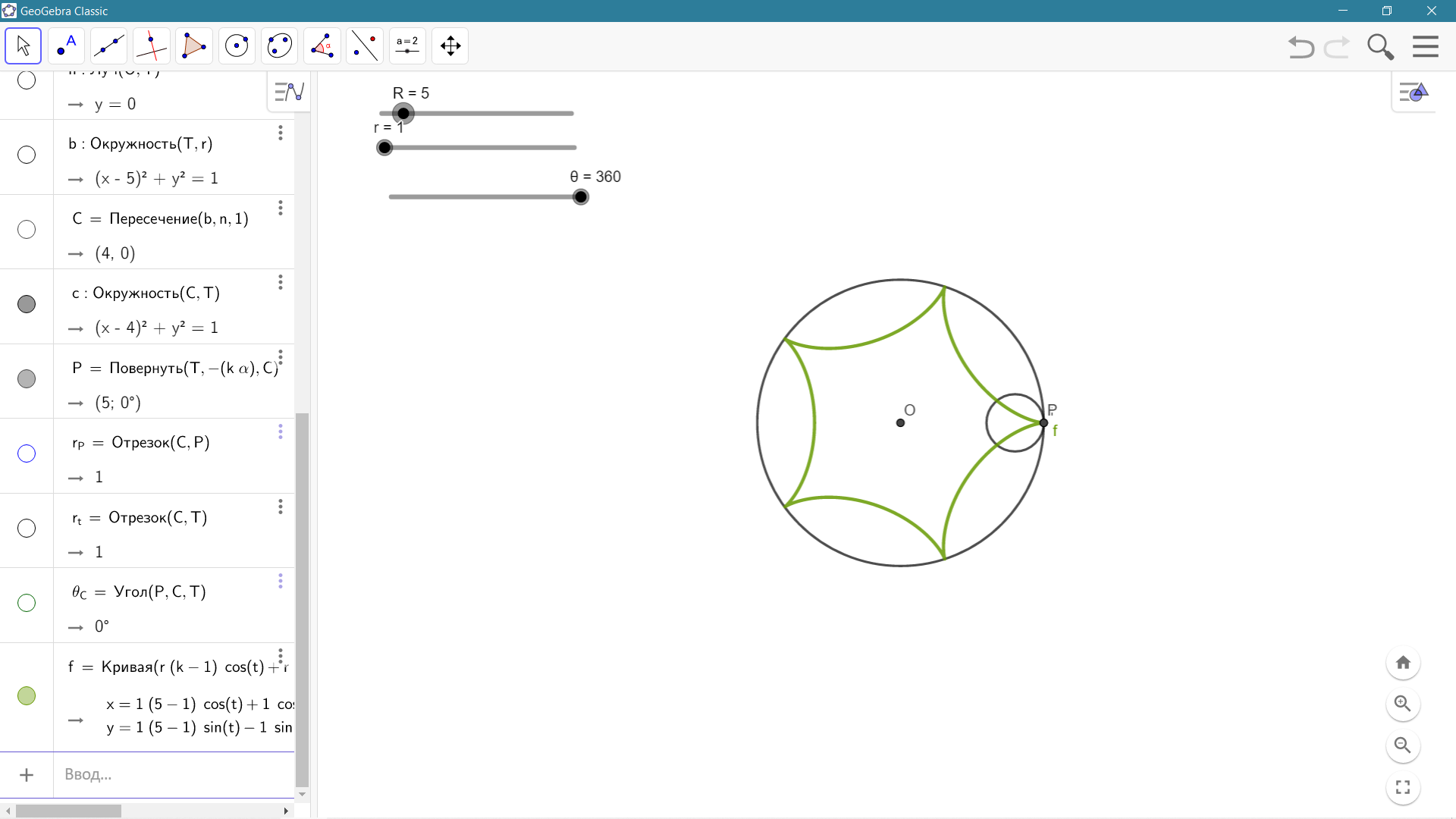
рис.4

рис.5
Отношение равно k. Пусть длина маленькой окружности равна c см. Тогда длина большой окружности равна ck см. Прокатываем маленький круг по большому кругу. За один оборот он прокатится по дуге длиной c см, за k оборотов он прокатится по дуге длиной ck см. И так как это равно длине большой окружности, то карандаш вернется в исходную точку.
Сделаем вывод: если отношение диаметров равно k, то гипоциклоида будет состоять из k дуг.