Отношение равно 5:2.
Окружность малого радиуса начала движение из точки А и сделал три оборота, точка P не вернулась в исходную точку, а остановился в точке В, которая лежит за точкой А. То есть малая окружность пошла на второй оборот по большой окружности. (рис.6)
рис.6
Далее она сделал четвертый и пятый обороты вокруг себя, после этого карандаш вернулся в исходную точку А: (рис.7)
рис.7
Итак, для того чтобы вернуться в начальную точку, малая окружность сделала 5 оборотов вокруг себя, прокатившись 2 раза по большой окружности.
Далее мы задали значения длин окружностей 60 см и 22 см и стали катать. У нас получилась такая гипоциклоида (рис.8):
рис.8
Окружность малого радиуса «прокатилась» по большой окружности несколько раз, а кривая все не смыкалась. Тогда мы решили выполнить расчеты, чтобы ответить на вопросы:
1) Сколько надо сделать оборотов окружности малого радиуса, чтобы гипоциклоида сомкнулась?
2) Сколько раз малая окружность прокатится по большой окружности?
Гипотеза: при любых целых значениях длин большой и малой окружности точка P вернется в исходное положение, и гипоциклоида сомкнется.
Расчеты: Зададим произвольные значения длин окружностей: например, 40 см и 12 см. Изобразим путь, по которому прокатывается малая окружность в виде прямой («распрямим» большую окружность). За один оборот окружность малого радиуса прокатывается на 12 см. За три оборота – на 36 см (точка P немного не доходит до точки A-исходного положения), дальше окружность начинает делать четвертый оборот и перекатывается за точку А. (рис.9)
рис.9
Для того чтобы проследить за её движением, отложим длину большого круга на прямой несколько раз. (рис.10)
рис.10
Итак, окружность малого радиуса перекатилась за точку А и продолжила движение на второй оборот по большой окружности, а затем на третий оборот. После этого точка P попадает в исходную точку А, из которой начала. Весь путь, по которому прокатилась малая окружность, равен 120 см. Это наименьшее натуральное число, которое делится на 40 и на 12. То есть наименьшее общее кратное чисел 12 и 40.
120:12=10, значит вокруг себя окружность малого радиуса сделала 10 оборотов;
120:40=3, значит по большой окружности прокатилась 3 раза.
Обобщим полученный результат: пусть длина большой окружности равна L см, длина малой равна l см. За один оборот малая окружность прокатывается на l см, за два оборота на 2 l см и т.д. Для того чтобы точка P вернулась в исходное положение, надо чтобы длина пути, по которому прокатывается окружность, делилась на l и на L. (рис. 11)
Таким образом, надо найти наименьшее натуральное число, которое делится на l и на L, то есть наименьшее общее кратное l и L.
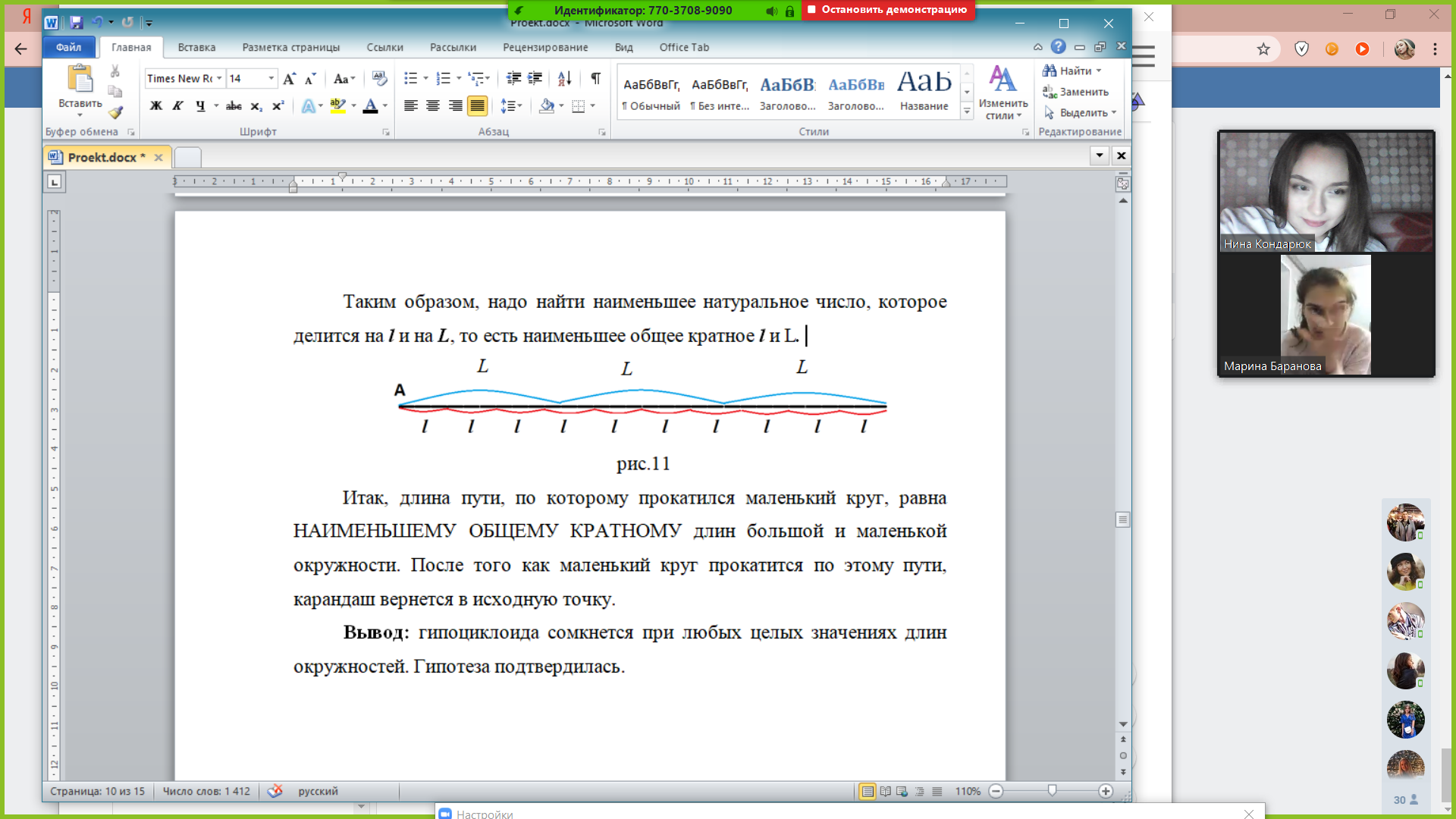
рис.11
Итак, длина пути, по которому прокатилась окружность малого радиуса, равна наименьшему общему кратному длин большой и малой окружности. После того как малая окружность пройдет по этому пути, точка P вернется в исходное положение.
Вывод: гипоциклоида сомкнется при любых целых значениях длин окружностей. Гипотеза подтвердилась.
Глава 2
Исследуем, как изменяется форма гипоциклоиды в зависимости от диаметра малой окружности.
Внутри большой окружности с диаметром 20 см мы перемещали окружности разного диаметра. На чертеже показаны гипоциклоиды, для следующих значений диаметра окружности малого радиуса: 4см, 5 см, 6,5 см. Как видим, при меньших значениях кривая имеет более вогнутую форму, с увеличением диаметра круга, кривая становится пологой.(рис.12)
рис.12
Стоит отметить, когда диаметр маленького круга ровно в 2 раза меньше диаметра большого круга: точка P начертила диаметр. (рис.13)
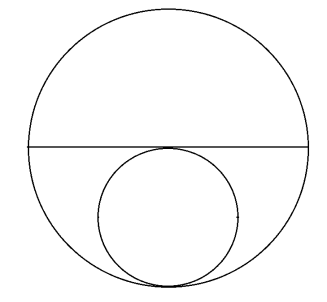
рис.13
Далее увеличим диаметр малой окружности. Гипоциклоида выгибается в другую сторону. (рис.14)
рис.14
Приведены чертежи для значений диаметра: 12; 15; 18 см. (рис.15)
рис.15
В результате получаем, что если внутри окружности диаметром 20 см прокатится окружность диаметром 15 см и 5 см, то гипоциклоиды получатся одинаковыми.
Гипотеза: гипоциклоиды получились одинаковыми, потому что сумма диаметров 15+5 равна диаметру круга, внутри которого движется малая окружность.
Подтверждение гипотезы: Рассмотрим движение окружности, диаметр которой равен 15 см.(рис.16) Она начала движение из точки А, прошла по дуге АВ (большей) и остановилась в точке В. Длина большой дуги АВ равна 
.
рис.16
Рассмотрим движение окружности диаметром 5 см.(рис.17) Остановимся в точке М.
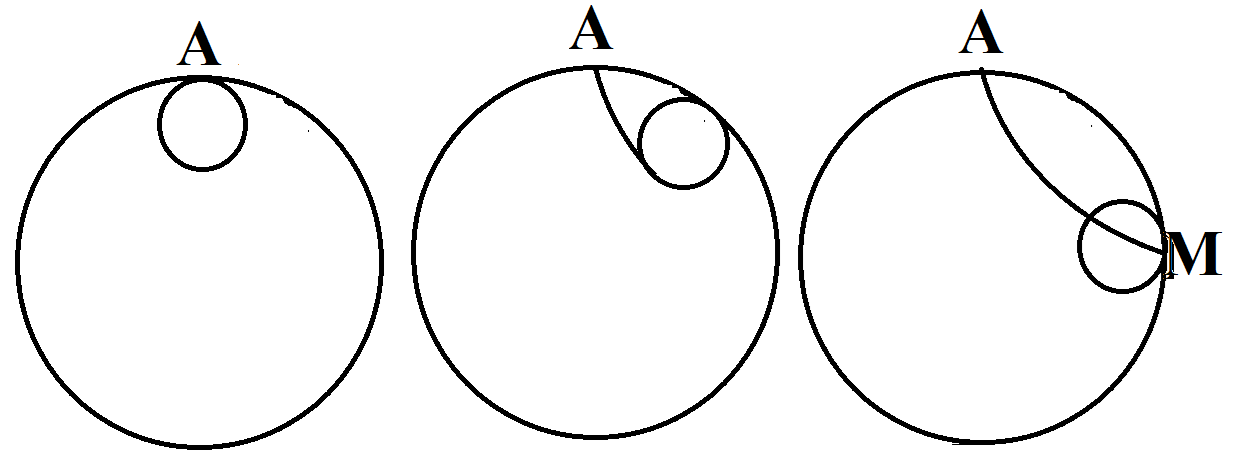
рис.17
Длина дуги АМ равна 
.
Сумма длин дуг равна 
. Также и длина большей окружности равна 
. То есть, сумма длин дуг АМ и АВ равна длине окружности, внутри которой происходит движение.Поэтому точки М и В совпадают.
Заключение.
С помощью интерактивной модели и расчетов мы исследовали, сколько дуг может иметь гипоциклоида, какую она имеет форму, и через сколько оборотов окружности малого радиуса она сомкнется.
Исходя из исследования, можно сделать следующие выводы:
1. Показано, что если отношение длин окружностей L:l равно целому числу, то гипоциклоида будет состоять из (L:l) дуг.
2. Показано, что для любых целых значений L и l гипоциклоида сомкнется.
3. Исследовано, как изменяется форма гипоциклоиды при различных значениях диаметра окружности малого радиуса.
4. Если диаметр окружности малого радиуса меньше, чем половина диаметра окружности большого радиуса, то гипоциклоида имеет вогнутую форму.
5. Если диаметр окружности малого радиуса равен половине диаметра окружности большого радиуса, то гипоциклоида имеет форму прямой.
6. Если диаметр окружности малого радиуса больше половины диаметра окружности большого радиуса, то гипоциклоида имеет вогнутую форму симметрично относительно диаметра.