Дифференциальные уравнения движения точки в векторной форме и в проекциях на декартовы и естественные оси координат.
Две основные задачи динамики материальной точки
Две основные задачи динамики материальной точки
Используя дифференциальные уравнения движения материальной точки (1.5), (1.10), (1.12) и (1.14), можно решить две основные задачи динамики точки, которые формулируют следующим образом.
Первая задача. Определить силы, действующие на точку, если известны масса точки и закон ее движения.
Решение этой задачи заключается, в основном, в определении ускорения точки по заданным уравнениям ее движения, т.е. в их дифференцировании.
Можно предложить такую последовательность решения задачи:
1) выбрать систему координат, в которой удобно решать данную задачу (декартовую или естественную);
2) изобразить в выбранной системе координат материальную точку в текущем положении;
3) приложить к точке активные силы и реакции связей;
4) записать основное уравнение динамики в проекциях на оси выбранной системы координат;
5) найти проекции ускорения точки на оси выбранной системы координат путем дифференцирования уравнений ее движения;
6) определить искомые параметры с помощью системы составленных уравнений.
Вторая задача. Определить закон движения точки, если заданы масса точки и действующие на нее силы.
Решение этой задачи требует интегрирования дифференциальных уравнений движения точки.
Методика решения второй задачи на примере декартовой системы координат состоит в следующем. Чтобы определить уравнения движения точки 
, необходимо дважды проинтегрировать систему трех дифференциальных уравнений 2-го порядка. В результате получим уравнения движения точки, содержащие, кроме времени, шесть произвольных постоянных. Уравнения движения точки и проекции ее скорости на оси координат имеют вид:
где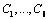 
– это так называемые постоянные интегрирования, которые находят из начальных условий. Начальные условия – значение скорости (проекций скорости) и положения (координат) точки в момент времени, обычно принимаемый равным нулю, которые должны быть предварительно заданы:
(1.16)
После определения постоянных интегрирования уравнения действительного движения точки окончательно получим в виде:
(1.17)
Решение второй задачи динамики можно выполнить в такой последовательности:
1) выбрать систему координат (декартовую или естественную), в которой удобно решать данную задачу;
2) изобразить в выбранной системе координат материальную точку в текущем положении;
3) приложить к точке активные силы и реакции отброшенных связей (если точка несвободна);
4) записать основное уравнение динамики в проекциях на оси выбранной системы координат;
5) проинтегрировать полученную систему дифференциальных уравнений и найти их общие решения;
6) определить, использую заданные начальные условия, постоянные интегрирования;
7) подставить постоянные интегрирования в общие решения и получить действительные уравнения движения точки.
4. Механической системой называют совокупность тел, выделенных из окружающего мира для последующего механического исследования.
5.Внешние силы - это такие силы, которые действуют только на поверхность предмета, но не проникают внутрь его. К этим силам относятся все силы, развиваемые материальным объектом.
Внутренние силы - это такие силы, которые действуют сразу на все атомы передвигаемого предмета независимо от того, где они находятся: на поверхности или в середине предмета. К этим силам относятся силы инерции и силы поля: гравитационного, электрического, магнитного. И происходит это потому, что поле и носитель инерции физвакуум свободно проникают внутрь любого тела.