Поляризация света.
Поперечность световой волны.
Попробуем, исходя из уравнений Максвелла, определить некоторые соотношения между векторами 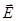 и
и 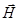 в плоской монохроматической волне, распространяющейся вдоль оси
в плоской монохроматической волне, распространяющейся вдоль оси 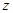 . В такой волне
. В такой волне 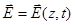 ,
,  . Из (1.3) следует:
. Из (1.3) следует:
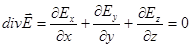
Но так как 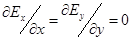 , то и
, то и 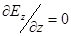 , то есть компонента
, то есть компонента 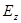 есть константа по координате
есть константа по координате 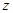 .
.
С другой стороны
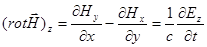 .
.
Рассуждая аналогично, приходим к выводу, что 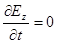 . Таким образом,
. Таким образом, 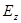 есть константа, ни от
есть константа, ни от 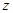 ,ни от
,ни от 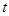 не зависящая. В быстропеременных полях (свет!) ее полагают нулевой. Проделав аналогичные выкладки для
не зависящая. В быстропеременных полях (свет!) ее полагают нулевой. Проделав аналогичные выкладки для 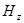 , имеем окончательно для плоской гармонической волны, бегущей вдоль оси
, имеем окончательно для плоской гармонической волны, бегущей вдоль оси 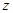 ,
, 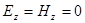 , а ненулевыми будут
, а ненулевыми будут 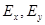 и
и 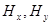 .
.
Далее из уравнений (1.1), (1.2) следует:
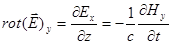
(2.1)
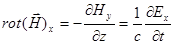 .
.
Аналогично для пары компонент  и
и 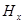 получим:
получим:
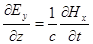 ;
; 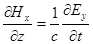 (2.2)
(2.2)
Выражения (2.1) и (2.2) описывают две независимые плоские волны, распространяющихся вдоль оси 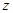 . Одна из них описывается взаимно – ортогональными компонентами
. Одна из них описывается взаимно – ортогональными компонентами 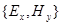 , другая -
, другая -  .
.
Плоские гармонические волны.
Рассмотрим более подробно случай 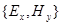 для плоской монохроматической волны. В этом случае:
для плоской монохроматической волны. В этом случае:
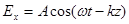 ,
, 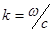 (2.3)
(2.3)
Используя (2.1)-(2.3) легко показать, что:
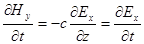 ,
, 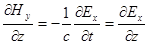 .
.
А это значит, что компоненты 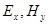 могут отличаться только на константу, которую, как и ранее, полагаем равной 0. Поэтому можно записать:
могут отличаться только на константу, которую, как и ранее, полагаем равной 0. Поэтому можно записать:
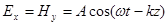 (2.4).
(2.4).
Соответствующая бегущая плоская гармоническая волна изображена на рис.2.1:
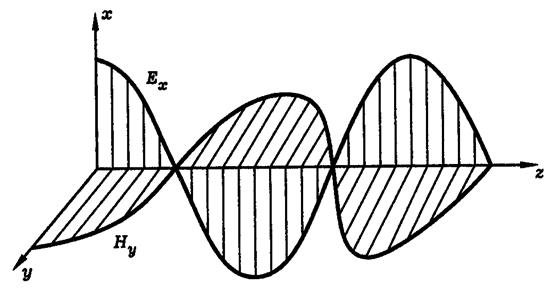
Рис.2.1. Плоская гармоническая волна 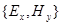
Для пары  получится
получится
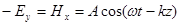 (2.5)
(2.5)
Состояния поляризации плоской монохроматической волны. Эллиптическая, круговая, линейная поляризации.
Только что рассмотренные волны вида 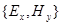 ,
,  называются плоско/линейно поляризованными, так как в фиксированной точке
называются плоско/линейно поляризованными, так как в фиксированной точке  конец вектора
конец вектора 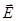 движется вдоль прямой. Введем также понятие плоскости поляризации – плоскости, в которой лежат вектора
движется вдоль прямой. Введем также понятие плоскости поляризации – плоскости, в которой лежат вектора 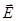 и орт
и орт 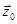 , характеризующий направление распространения волны.
, характеризующий направление распространения волны.
Такая «несправедливость» в выделении вектора 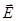 обусловлена тем, что при взаимодействии световой волны с веществом/ зарядом описывается выражением
обусловлена тем, что при взаимодействии световой волны с веществом/ зарядом описывается выражением 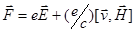 , из которого следует, что при нерелятивистских скоростях
, из которого следует, что при нерелятивистских скоростях 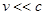 влияние магнитного поля намного меньше, чем электрического. Экспериментально это подтверждается опытами Винера.
влияние магнитного поля намного меньше, чем электрического. Экспериментально это подтверждается опытами Винера.
В силу принципа суперпозиции решением волнового уравнения в общем случае будет волна, у которой обе компоненты  и
и  отличны от нуля, то есть волна вида:
отличны от нуля, то есть волна вида:
 (2.6)
(2.6)
Положим компоненты поля 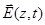 гармоническими:
гармоническими:
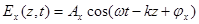 ,
, 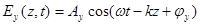
 (2.7)
(2.7)
задача состоит в ом, чтобы найти выражение, описывающее траекторию конца вектора 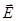 в плоскости
в плоскости  . Для этого в (2.7) исключим зависимость от времени, для чего введем обозначение
. Для этого в (2.7) исключим зависимость от времени, для чего введем обозначение 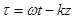 и преобразуем
и преобразуем 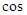 - функции суммы углов:
- функции суммы углов:
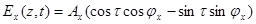
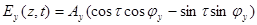
Откуда
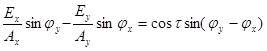

Возводя в квадрат и складывая, получим окончательно:
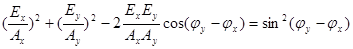 (2.8)
(2.8)
Последнее выражение описывает эллипс, показанный на рис.2.2.
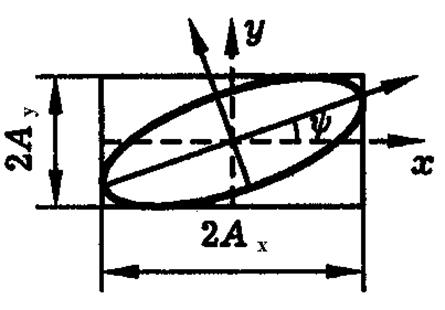
Рис.2.2 Эллипс поляризации.
Это означает, что конец вектора 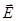 в плоскости
в плоскости  движется по эллипсу. Поэтому в общем случае плоская монохроматическая волна является эллиптически поляризованной.
движется по эллипсу. Поэтому в общем случае плоская монохроматическая волна является эллиптически поляризованной.
Конец вектора 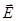 может вращаться как по, так и против часовой стрелки. Если для наблюдателя, смотрящего навстречу пучку, вектор
может вращаться как по, так и против часовой стрелки. Если для наблюдателя, смотрящего навстречу пучку, вектор 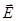 вращается по/ против часовой стрелке/ стрелки, то говорят о правой/ левой поляризации. Можно показать, что направление вращения определяется разностью фаз
вращается по/ против часовой стрелке/ стрелки, то говорят о правой/ левой поляризации. Можно показать, что направление вращения определяется разностью фаз 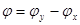 . Если
. Если 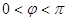 , то имеет место правая поляризация, а если
, то имеет место правая поляризация, а если  , то левая. Теперь разберем частные случаи в (2.8).
, то левая. Теперь разберем частные случаи в (2.8).
Линейная поляризация. Если 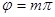 , где
, где 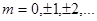 , то эллипс вырождается в прямую, описываемую уравнением
, то эллипс вырождается в прямую, описываемую уравнением
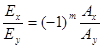
Для  и
и 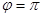 соответствующая картинка показана на рис.2.3.
соответствующая картинка показана на рис.2.3.

Рис.2.3. Линейная поляризация световой волны.
Круговая поляризация. Если 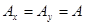 и
и 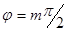 , где
, где  , то получим окружность:
, то получим окружность:
 ,
,
причем различаются правая и левая циркулярные поляризации. (См. рис.2.4).

Рис.2.4. Поляризованная по левому и правому кругу световые волны.
Можно показать, что сумма право и лево поляризованной волн одинаковой амплитуды дают линейную поляризацию.