В общем случае параметры эллиптической поляризации полностью описываются тройкой параметров  или же выражающимися через них полуосями эллипса
или же выражающимися через них полуосями эллипса  и наклоном большой оси к оси абсцисс
и наклоном большой оси к оси абсцисс  :
:  .
.
Можно также характеризовать состояние поляризации электромагнитной волны с помощью так называемых параметров Стокса, определенных следующими формулами:
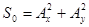
 (2.9)
(2.9)
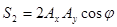

Так как  , то независимыми являются только три из четырех параметров. Если ввести вспомогательный угол
, то независимыми являются только три из четырех параметров. Если ввести вспомогательный угол  , определяемый выражением
, определяемый выражением  (знак + соответствует правой, а – левой поляризации), то можно получить следующее выражение для параметров Стокса:
(знак + соответствует правой, а – левой поляризации), то можно получить следующее выражение для параметров Стокса:
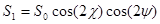
 (2.10)
(2.10)

На основе формул (2.9, 2.10) можно характеризовать поляризацию световой волны наглядным геометрическим способом. При этом параметры Стокса  интерпретируются, как декартовы координаты точки, лежащей на поверхности сферы радиуса
интерпретируются, как декартовы координаты точки, лежащей на поверхности сферы радиуса  . Углы
. Углы 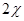 и
и  имеют смысл сферических угловых координат этой точки. (См. рис.2.5):
имеют смысл сферических угловых координат этой точки. (См. рис.2.5):
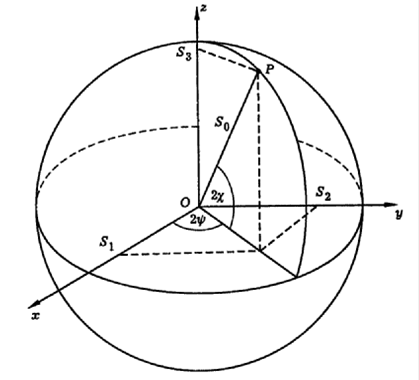
Рис.2.5. Сфера Пуанкаре.
Комплексное представление световой волны. Произвольная плоская монохроматическая волна.
Используя формулу Эйлера
 (2.11)
(2.11)
можно плоскую гармоническую волну

представить в виде:
 (2.12)
(2.12)
Здесь к.с. обозначает комплексное сопряжение, а величины  и
и  получили название комплексных амплитуд.
получили название комплексных амплитуд.
Для линейно - поляризованной волны имеем:
 , (2.13)
, (2.13)
где  - комплексная амплитуда,
- комплексная амплитуда,  - орт в направлении поляризации (вектор поляризации).
- орт в направлении поляризации (вектор поляризации).
Такая запись волнового поля сейчас широко используется в оптике, так как автоматически верно учитывает все члены, появляющиеся в нелинейных взаимодействиях и удобна в случае, когда используют преобразование Фурье.
Пусть плоская монохроматическая волна бежит в произвольном направлении, определяемом ортом  . Это означает, что волновые фронты, имеющие вид плоскостей, ортогональны этому орту (см. рис.2.6).
. Это означает, что волновые фронты, имеющие вид плоскостей, ортогональны этому орту (см. рис.2.6).
Введем новый вектор, именуемый волновым:  (2.14)
(2.14)
Согласно последнему выражению, этот вектор указывает направление распространения волны, а его модуль равен волновому числу 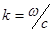 .
.

Рис.2.6. Плоская волна, бегущая в направлении орта  .
.
Если теперь обозначить через  расстояние, пройденное волной вдоль
расстояние, пройденное волной вдоль  , а через
, а через  - радиус-вектор произвольной точки волнового фронта, то из рисунка следует, что
- радиус-вектор произвольной точки волнового фронта, то из рисунка следует, что  и
и
 .
.
Теперь в принятых обозначениях можно записать для поля плоской линейно - поляризованной монохроматической волны
 (2.15)
(2.15)
В аналогичной форме представимо и магнитное поле волны:
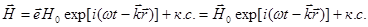 (2.16)
(2.16)
Внимание! В целом ряде монографий/ учебников принята запись  . При этом полагается, что реально берется только действительная часть данного выражения так же, как это принято в электротехнике. Такая запись вполне пригодна в линейной оптике.
. При этом полагается, что реально берется только действительная часть данного выражения так же, как это принято в электротехнике. Такая запись вполне пригодна в линейной оптике.
Используя введенные обозначения, получим для плоской монохроматической волны, распространяющейся в произвольном направлении, соотношения, связывающие вектора  .
.
Введем векторный дифференциальный оператор
 (2.17)
(2.17)
Тогда уравнения Максвелла в вакууме примут вид:
 ,
,  (2.18)
(2.18)
 ,
, 
Рассмотрим действие операторов дифференцирования по координате и по времени на множитель  :
:
 , где
, где 

Поэтому для вектора 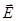 получим (для
получим (для 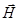 выражения полностью аналогичны):
выражения полностью аналогичны):

 (2.19)
(2.19)

С учетом этих выражений уравнения Максвелла (2.18) примут следующий вид:
 ,
, 
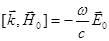 ,
, 
Заменяя  в соответствии с (2.14), получим наиболее простую запись:
в соответствии с (2.14), получим наиболее простую запись:
 ,
,  (2.20)
(2.20)
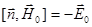

Теперь комбинируя (2.15), (2.16), (2.20), получим векторные формулы, определяющие структуру произвольной плоской монохроматической волны:
 ,
, 
 ,
, 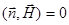 (2.21)
(2.21)
Равенство 0 соответствующих скалярных произведений выражают свойство поперечности световой волны в свободном пространстве: т.е. вектора 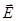 и
и 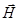 перпендикулярны направлению распространения.
перпендикулярны направлению распространения.
Соответствующие векторные произведения показывают, что вектора  ,
, 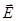 ,
, 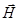 образуют правую тройку так, как это показано на рис.2.7.
образуют правую тройку так, как это показано на рис.2.7.

Рис.2.7 Структура поля плоской монохроматичной световой волны.
Немонохроматический свет. Естественная поляризация.
Как уже говорилось, излучение реальных нелазерных источников весьма непохоже на регулярные, например плоские, волны. Для света, излучаемого такими источниками характерны хаотические колебания вектора 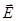 в плоскости волнового фронта. При этом все возможные направления этих колебаний равновероятны. Поэтому говорят о неполяризованном/ естественно поляризованном свете.
в плоскости волнового фронта. При этом все возможные направления этих колебаний равновероятны. Поэтому говорят о неполяризованном/ естественно поляризованном свете.
Поле такой волны (плоской, немонохроматической) может быть представлено в виде:
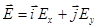

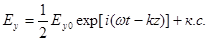
Здесь комплексные амплитуды  и
и  надо рассматривать, как случайные функции времени.
надо рассматривать, как случайные функции времени.
Введем понятие матрицы когерентности световой волны:
 (2.22)
(2.22)
Здесь символ  означает усреднение по времени. Матрица полностью характеризует состояние поляризации плоской немонохроматичной волны. Элементы этой матрица могут быть измерены экспериментально.
означает усреднение по времени. Матрица полностью характеризует состояние поляризации плоской немонохроматичной волны. Элементы этой матрица могут быть измерены экспериментально.
Экспериментальные методы измерения поляризации.
Для измерения состояния поляризации светового пучка используются приборы, именуемые поляризаторами/ анализаторами. Реально они могут использовать различные физические принципы для своего функционирования, но суть их состоит в том, что такое устройство пропускает свет без потерь только при условии, что падающая волна – линейно поляризована и вектор 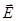 лежит в некоторой выделенной плоскости, именуемой плоскостью пропускания поляризатора. При повороте вокруг оси, совпадающей с направлением распространения света, на
лежит в некоторой выделенной плоскости, именуемой плоскостью пропускания поляризатора. При повороте вокруг оси, совпадающей с направлением распространения света, на  поляризатор полностью блокирует падающее на него излучение. Таким образом, экспериментально определить то, что свет линейно поляризован, можно при помощи единственного прибора.
поляризатор полностью блокирует падающее на него излучение. Таким образом, экспериментально определить то, что свет линейно поляризован, можно при помощи единственного прибора.
Ситуация усложняется в случае, если свет поляризован эллиптически/ неполяризован. Здесь приходится использовать компенсаторы, то есть приборы, преобразующие эллиптически поляризованный свет в линейно поляризованный по заданному закону. Подробно на вопросе измерения параметров поляризации остановимся в соответствующем месте нашего курса.