Если считать, что магнетизм обусловлен северными и южными магнитными массами (представления, господствовавшие до 20-ых годов 19 века), то характер взаимодействия этих масс в точности повторяет закон взаимодействия точечных зарядов в электростатике (сила взаимодействия электрических и магнитных зарядов направлена по полю). Однако, ситуация изменяется кардинальным образом, если считать, что магнитное поле создается проводниками с током: если поместить проводник с током в магнитное поле, то сила, действующая на проводник направлена не по полю, а перпендикулярно ему.
Для определения величины силы, действующей на проводник с током со стороны магнитного поля, следует поместить прямоугольный контур с током в однородное магнитное поле, откуда
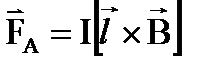
Направление силы Ампера определяется по правилу буравчика: силовые линии поля входят в ладонь, четыре пальца показывают направление тока. Тогда отогнутый большой палец укажет направление силы.
Выражение для силы Ампера в дифференциальной форме
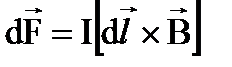
Закон Био-Савара-Лапласа. Лаплас, анализируя результаты экспериментов Био и Савара, предложил способ отыскания величины индукции магнитного поля, создаваемого отрезками проводников с током произвольной конфигурации: для определения величины В необходимо разбить проводник на малые, элементарные участки d 
и затем найти векторную сумму элементарных индукций d 
, создаваемых всеми участками проводника.
Id 
|
|
d 
|
| + |
|
Индукция магнитного поля в
центре кругового тока 
| + |
| r0 |
| α1 |
| α2 |
|
|
Индукция магнитного поля,
создаваемая прямым 
Проводником с током
Магнитное взаимодействие параллельных токов.
| F |
| I1 |
| I2 |
| I1 |
F- сила, действующая на единицу длины одного проводника, со стороны магнитного поля, создаваемого всем другим проводником.
.
Из этого выражения следует определение единицы измерения силы тока:
Один ампер - это сила постоянного тока, текущего по каждому из двух параллельных, бесконечно длинных проводников бесконечно малого кругового сечения в вакууме на расстоянии 1 метр, и создающая силу взаимодействия между ними 2×10−7 Н на каждый метр длины проводника.
Теорема о циркуляции вектора В.
Циркуляция вектора В магнитного поля, создаваемого прямым проводником с током I, по окружности радиуса R
Оказывается, что этот результат справедлив и для случая проводника с током и замкнутого контура интегрирования произвольных форм.
Используя принцип суперпозиции: Циркуляция вектора магнитной индукции равна алгебраической сумме токов, охватываемых контуром интегрирования, умноженной на μ0.
Поле бесконечно длинного
Соленоида
где n- число витков, приходящееся
на единицу длины соленоида
Поле тороида
где N- общее число витков
Магнитное поле, создаваемое движущимся зарядом. Следуя историческому развитию теории магнетизма, найдем выражение для индукции магнитного поля, создаваемого движущимся зарядом, опираясь на закон Био-Савара-Лапласа – выражение для индукции магнитного поля, создаваемого элементом тока I d 