Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:
Физический смысл потенциальной энергии деформированного тела
Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Задачи
1. Какую работу совершает сила тяжести, действующая на дождевую каплю массой 20 мг, при ее падении с высоты 2 км?
Дано:
m = 20 мг = 20· 10-6 кг
h = 2 км = 2 ·103 м
Найти: Ат
Решение:
Работа сила тяжести находится по формуле: А= – (Ер2 – Ер1),т.к. потенциальная энергия тела, находящегося на поверхности земли равна нулюЕр2 = 0, то выражение можно записать:: А= – Ер1 = m∙g·h = 20· 10-6 · 2 ·103 · 9,8 = 0.39 Дж.
2. Какую работу совершает человек при поднятии груза массой 2 кг на высоту 1 м с ускорением 3 м/с2?
Решение:
Работа при перемещении груза на высоту h равна: A = F · h (1)
Сила, с которой необходимо тянуть вверх груз заданной массы определяется согласно 2-му закону Ньютона: ma = F - m g
F = m (a + g)
Подставляем в формулу (1): А = m h (a + g) = 2· 1 ·(3 + 9,8) = 26 Дж.
Кинетическая энергия
Для начала рассмотрим простой случай движения, при котором сила, действующая на тело, и скорость тела направлены вдоль одной и той же прямой (см. рис. 2).
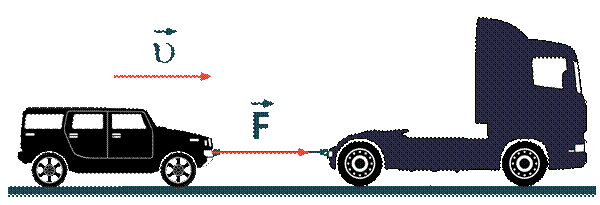
Рис. 2. Пример, при котором сила и скорость тела направлены вдоль прямой
С одной стороны, действующая на тело сила сообщает ему ускорение, то есть изменяет его скорость, с другой стороны, эта сила совершает над телом некоторую работу, поскольку тело под этой силой совершает некоторое перемещение. Следовательно, между изменением скорости тела и работой силы должна существовать связь.
Для проведения расчетов направим координатную ось в ту сторону, куда направлены скорость и сила, тогда проекции силы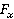 
, ускорения 
, перемещения 
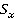и скорости 
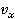будут равны просто модулям этих векторов (см. рис. 3):
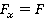
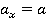
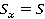
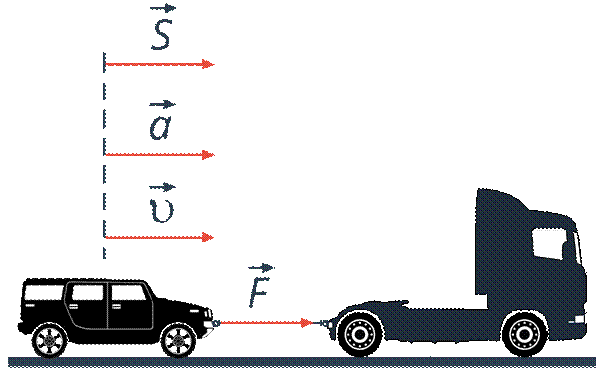
Рис. 3. Направление оси Ох, а также других величин
В этом случае формула для работы силы будет иметь простой вид:
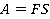
Второй закон Ньютона, записанный на языке проекций, будет иметь стандартный вид:
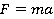
Если движение носит равноускоренный характер, то есть сила не зависит от времени и координат, то работу с учетом приведенных формул можно представить в виде:
,
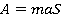где S – модуль перемещения. Для того чтобы связать изменение скорости с работой силы, вспомним кинематику, а точнее формулу, связывающую модуль перемещения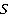 
с ускорением 
и скоростями тела в начальный и конечный моменты времени (формула с исключенным временем):
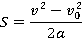
Подставив это выражение в формулу для работы, получим:
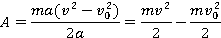
Эта формула связывает квадрат скорости с работой силы. Обратим внимание на величины, которые стоят в правой части этого равенства. И уменьшаемое, и вычитаемое представляют собой половину произведения массы тела на квадрат его скорости, причем в уменьшаемое входит квадрат конечной скорости, в вычитаемое – квадрат начальной скорости тела.
Величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
Теорема об изменении кинетической энергии
Последнее равенство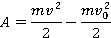 
говорит о том, что работа силы, действующей на тело, равна разности между кинетической энергией в конечный момент времени и кинетической энергии в начальный момент времени. Сформулируем последнее утверждение более строго: работа силы или равнодействующей всех сил равна изменению кинетической энергии тела:
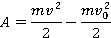
Данное выражение называется теоремой об изменении кинетической энергии. Проанализируем эту теорему. Когда сила, действующая на тело, направлена в сторону движения тела и, следовательно, совершает положительную работу (см. рис. 4), то конечная кинетическая энергия больше, чем начальная кинетическая энергия:
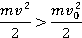
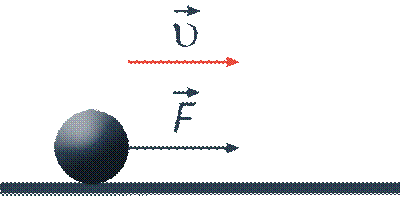
Рис. 4. Сила направлена в сторону движения тела
Этот результат означает, что в данном случае кинетическая энергия тела увеличивается. Это вполне логичный вывод, поскольку сила сонаправлена со скоростью, то модуль скорости должен увеличиваться. Также совершенно очевидно, что в противоположном случае, когда сила направлена в противоположную сторону скорости, то кинетическая энергия тела должна уменьшаться (см. рис. 5).
Рис. 5. Сила противонаправлена скорости
Сделаем еще два небольших вывода из теоремы:
1. Кинетическая энергия измеряется в джоулях 
.
2. Мы вывели данную теорему, основываясь всего лишь на втором законе Ньютона, это означает, что сама по себе теорема об изменении кинетической энергии является иначе сформулированным вторым законом Ньютона.
Это позволяет нам утверждать, что она справедлива в случае действия сил, которые мы знаем. То есть мы ее можем применять в случае действия силы упругости, силы тяжести, силы трения…
Вернемся к вопросу о том, каким же образом введенная нами физическая величина позволяет упростить нам решение механических заданий. Здесь сделаем одно очень важное замечание: несмотря на то что мы доказали выше приведенную теорему в предположении о равноускоренном характере движения тела, ее формулировка остается справедлива и в том случае, когда равнодействующая всех сил не является постоянной величиной. Вернемся к нашей модельной задачи. Для расчета скорости тела на вершине горки у нас теперь нет необходимости знать величины сил тяжести и реакции опоры в каждой точке траектории (см. рис. 6).
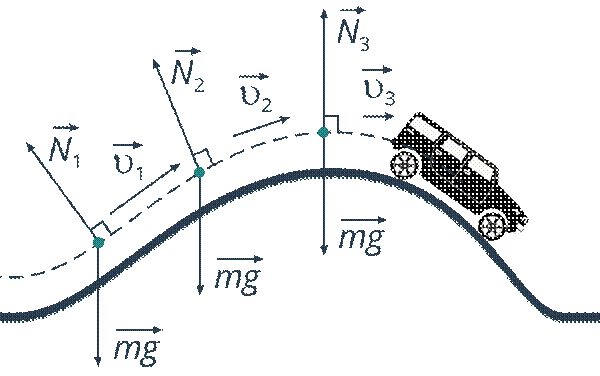
Рис. 6. Действие сил в каждой точке траектории
Нам достаточно вычислять работу сил, приложенных к телу, и знать скорость тела до попадания на горку. Владея значениями этих величин и применив теорему об изменении кинетической энергии, мы сразу получим скорость в верхней точке траектории тела (см. рис. 7).
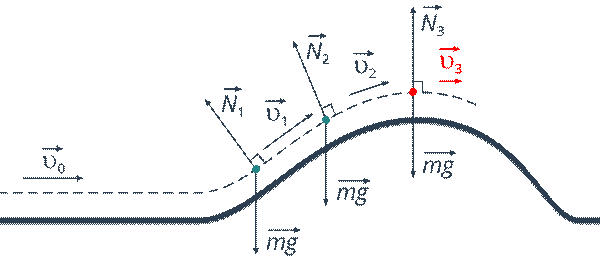
Рис. 7. Скорость тела в верхней точке
Если разбить траекторию движения на маленькие участки, то легко заметить, что, поскольку сила реакции опоры в любой точке перпендикулярно поверхности, ее работа на каждом малом перемещении будет равна 0 (см. рис. 8), а, следовательно, будет равна 0 на всей траектории движения:
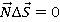
Рис. 8. Траектория, разбитая на маленькие части
Остается сила тяжести, которую мы научимся вычислять на следующих уроках.
Сделаем еще два замечания относительно кинетической энергии.
1. Если мы действуем на тело с некоторой силой и совершаем при этом механическую работу, то кинетическая энергия данного тела обязательно изменится, при этом, во-первых, для тел разной массы мы можем добиться одного и того же изменения кинетической энергии, если совершим над ними одинаковую работу.
2. Одной и той же работы или одного и того же изменения кинетической энергии мы можем добиться либо действуя на тело большой силой на маленьком перемещении, либо действуя с маленькой силой на большом перемещении тела.
Замечание второе. До сих пор мы говорили только об изменении кинетической энергии, а какой же смысл у кинетической энергии самой по себе? Представим следующую ситуацию: у нас имеется изначально покоившееся тело, то есть начальная скорость 
равна 0. Нам необходимо при помощи некоторой силы разогнать данное тело до скорости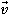 
, при этом понятно, что сила должна совершить некоторую механическую работу. Чему же равна эта работа?
Согласно теореме об изменении кинетической энергии работа равна разности конечной и начальной кинетических энергий, при этом начальная кинетическая энергия равна 0, поскольку начальная скорость равна 0, и тогда:
Следовательно, кинетическая энергия тела массой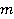 
, движущегося со скоростью 
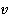, равна работе, которую нужно совершить, чтобы сообщить телу эту скорость. Точно такую по модулю, но противоположную по знаку работу нужно совершить, чтобы остановить тело, которое изначально двигалось со скоростью 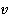. Далее из теоремы об изменении кинетической энергии следует, что данная физическая величина характеризует лишь движущиеся тела, при этом изменение кинетической энергии равно работе равнодействующей сил, действующих на тело.