На рис. 2 показан замечательный процесс многоэтапного замораживания, который происходит в изотермических условиях в течение времени (10 с) для сантиметровых пузырьков. Первоначальный режим замораживания представлял собой восходящий фронт замораживания, аналогичный восходящему замораживанию сидячих капель, но более дендритный по внешнему виду. Непосредственно при контакте с ледяной подложкой пузырь показал восходящий поток со скоростью v ≈ 10 мм с −1, исходящий из фронта раннего замерзания (рис. 2а, б и дополнительные рис. 3 и 4). В течение миллисекунд этот поток дестабилизировался в перья с радиусом R p ~ 1 мм. После типичного времениОО{\ cal {O}} {\ cal {O}}ОО (1 с), кристаллы льда диаметром около 100 мкм внезапно стали видимыми и были вовлечены в восходящий поток жидкости. Сотни этих увлеченных ледяных кристаллов драматически закручивались вокруг пузыря, который мы называем «эффектом снежного шара». Через несколько секунд перья рассеялись и вымерли, когда кристаллы льда стали больше. Наконец, пузырь полностью замерз в течение (10 с) не только с восходящего фронта замораживания, но и особенно с плавающих ледяных кристаллов, когда они росли и сцеплялись вместе.
Рис. 2
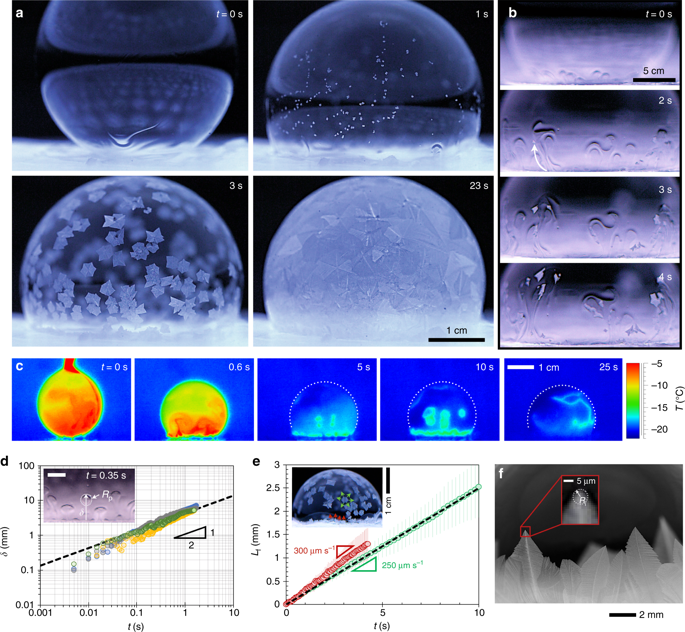
Замораживание пузырьков в охлажденных и изотермических условиях. Замораживание пузырька 10 мл осажденного на ледяной диск (Дополнительный рис. 3) в прогулке в морозильной камере охлаждают до T ∞ = -18,5 ± 0,5 ° С при относительной влажности 60 ± = 5%. b Фронт замораживания вызвал поток Марангони, который оторвал и увлек некоторые растущие частицы льда. c Промежуточные термографические изображения, где пунктирные дуги проясняют интерфейс пузырька и воздуха. Части жидкости пузырька принимали температуру морозильной камеры вскоре после осаждения, в то время как фронты замораживания были теплее (то есть около температуры плавления) из-за выделения скрытой теплоты. Коэффициент излучения льда был откалиброван при ε = 0,98. Нулевой момент времени соответствует первому контакту пузырька с ледяной подложкой, где его верх все еще прилипает к пипетке (первые кадры a - c). d Смещение (δ) четырех тепловых шлейфов (разных цветов) измеряли во времени, когда T w ≈ T ∞ = −19,6 ° C. На вставке видно, что радиус шлейфов был порядка R p ~ 1 мм. Шкала представляет 2 мм. e Скорость роста фронтов замерзания, исходящих от субстрата (красные точки данных, v i ≈ 300 мкм с -1) или от кристаллов льда, взвешенных в жидкой пленке (зеленый, v i ≈ 250 мкм с -1), когда T ∞ = −18,4 ± 1,7 ° C. Столбики ошибок представляют собой стандартное отклонение от среднего значения трех испытаний. f Радиус льда, R i, был оценен по верхушке кристаллов льда, растущих из подложки
Возможные механизмы: Механизм вертикальных шлейфов, возникающих при контакте пузыря с ледяной поверхностью, далеко не очевиден. Можно предусмотреть по меньшей мере четыре типа потоков: поток Марангони из-за неоднородных концентраций поверхностно-активного вещества, поток из-за неоднородной кривизны поверхности (предельная регенерация), плавучий поток из-за тепловых эффектов или тепловой поток Марангони, вызванный скрытой теплотой плавления. Первые два механизма потока не требуют температурного градиента и поэтому могут быть оценены с использованием пузырьков, нанесенных на сухой субстрат в условиях комнатной температуры (рис. 3а). Распределение поверхностно-активного вещества вдоль границы раздела можно изолировать, рассматривая объемную подвесную каплю, подвешенную на воздухе, где для достижения стационарного поверхностного натяжения требовалось около 40 минут (дополнительная рис. 1). Однако следует помнить, что наши мыльные пузыри имеют толщину всего около 1 мкм. Для таких тонких пленок, имеющих большое отношение площади поверхности к объему, диффузия поверхностно-активного вещества к свободной поверхности должна быть намного быстрее 32. Например, соотношение диффузионных временных масштабов между подвесной каплей и пузырем равно ~ 10 6, так что устойчиво Поверхностное натяжение состояния должно быть достигнуто в течение примерно 1 мс для пузырька. Напротив, мы наблюдали, что пузырьки комнатной температуры на сухих субстратах генерировали шлейфы в течение очень длительного промежутка времени (10 мин) (дополнительная рис. 5р2д г о р/е20рdроп2/е02{\ cal {O}}ОО), исключая асимметричные концентрации ПАВ в качестве вероятного механизма. Кроме того, поверхностное натяжение, измеренное с подвесной каплей, изменялось только во времени, а не в пространстве, поскольку измеренная кривизна указывала на одно значение поверхностного натяжения в любой данный момент времени (дополнительная рис. 1).
Рис. 3

Контрастные механизмы для плюмов в незамерзающих и замерзающих пузырьках. a Для пузырька, осажденного на сухой подложке комнатной температуры, шлейфы непрерывно генерировались в течение ~ 10-минутного срока службы пузырька из-за незначительной регенерации. b Для пузырька, осажденного на ледяной холодной стадии (T w = -20 ° C), восходящий фронт замораживания (красные стрелки) подавлял предельную регенерацию, но позволял короткий (~ 1 с) поток из-за замерзания Марангони. В любом случае здесь условия окружающей среды были T ∞ ≈ 25 ° C с относительной влажностью RH ≈ 19%.
Второй механизм предельной регенерации, предложенный Мисселсом, Шинодой и Франкелем 33, впервые является чисто геометрическим и обязан своим происхождением жидкому мениску у основания пузыря. Разница давлений Лапласа между пузырем и мениском создает долгоживущие перья 10, 34. Это согласуется с нашим контрольным случаем пузырьков комнатной температуры, в котором шлейфы поддерживались в течение большей части срока службы пузырька (рис. 3а и дополнительная рис. 5а).). Хотя мы можем поэтому приписать плюмы в пузырьках комнатной температуры к предельной регенерации, это не обязательно объясняет плюмы в замерзающих пузырьках. В случае замерзания жидкий мениск будет затвердевать снизу вверх замораживающим фронтом в течение примерно 0,1 с (дополнительная рис. 4d), что остановит предельную регенерацию. Принимая во внимание, что отмечалось, что перья сохраняются в течение нескольких секунд для замерзающих пузырьков, мы должны вместо этого рассмотреть тепловые механизмы плавучести или потока Марангони из-за скрытой теплоты, выделяющейся с фронта замораживания.
Предыдущая работа показала, что плавучие тепловые перья могут образовываться в вертикальных мыльных пленках, где перья были в основном инерционными 35. Инерция в нашей системе пренебрежимо мала, так как число Рейнольдса равно Re = ρV 2 / (ηV / e 0) = ρVe 0 / η, где η ≈ 2 × 10 -3 Па с - вязкость воды 36 при −6,5 ° C., Для типичных значений V ~ 10 мм с -1, измеренных путем наблюдения начальной скорости восходящего факела (рис. 2d), получаем Re ~ 0,01. Поэтому плавучий поток в наших мыльных пузырях должен был бы уравновесить градиент давления Δρg с градиентом вязкого напряжения. Для типичного значения Δ ρ ~ 1 кг м -3 это приводит к плавучим потокам скорости нм с -1. Это в отличие от рис. 2d, где скорость не постоянна во времени и примерно на шесть порядков быстрее (V ~ 10 мм с -1).ηВ/е20ηВ/е02V _ {\ mathrm {B}} \ sim \ Delta \ rho ge_0 ^ 2 {\ mathrm {/}} \ eta \ sim 10ВВ~ Д р ге20/ η∼ 10ВВ~Δρграмме02/η~10
Это оставляет нам окончательную возможность возникновения потока Марангони, вызванного скрытым теплом, выделяемым при замерзании. Мы будем называть этот процесс «заморозкой марангони». Нагрев, вызванный замерзанием, вызывает градиент поверхностного натяжения, γ / δ, где δ - масштаб длины градиента температуры, приводящего поток в движение. Это должно быть уравновешено вязкими напряжениями, ηV М / (б + е 0 /2), где V М является скорость Марангони, б длина скольжения Пуазейля идет по пленке пузыря (Дополнительный рис. 6), а профиль скорости был аппроксимирован как постоянный наклон. Для нашей системы мкм 8, t d ~ 10 3 с шкала времени дренирования сантиметрового пузырька, которая наблюдалась экспериментально (дополнительная рис. 5а). Поэтому (b + e 0/2) ~ e 0, что приводит к упрощенному вязкому напряжению, гдеб = пR / (ρ гTd)--------√∼ 1бзнак равноηр/(ρграммTd)~1ηδ˙/е0ηδ˙/е0δ˙= d δ/ дт=VMδ˙знак равноdδ/dTзнак равноВMпредставляет скорость шлейфа. Относительное напряжение поверхностного натяжения и вязкое напряжение и решение для δ:
δ∼ 2 Δ γе0η------√T1 / 2,δ~2Δγе0ηT1/2,
(2)
Обратите внимание, что Δ γ ≈ 2 мН м -1 для Δ T = T m - T l ≈ 13,5 ° C, что соответствует нашей степени переохлаждения (рис. 2c) 37. При сравнении уравнения. 2 для экспериментов, траектории тепловых плюмов отслеживались для пузырьков Ω = 10 мл (рис. 2г). Измерения δ находятся в хорошем соответствии с 1/2-законом с числовым предварительным множителем 1,6, подтверждая механизм замораживания Марангони для потока в замерзающих пузырьках. Наконец, базовая физика для полученной длины волны и радиуса плюма (R p~ 1 мм) нетривиальны и выходят за рамки этого исследования, как было отмечено ранее в феномене взрыва Марангони 38.
Замораживание Марангони и «эффект снежного шара»: Замораживание Марангони происходит, когда потоки Марангони могут быть вызваны замерзшим нагревом на линии контакта, и эти потоки доминируют над любым другим возможным потоком. Два температурных требования для замораживания Марангони включают в себя условие для замерзания: T w < T m и условие для вертикально восходящего потока Марангони: d T / d z <0, так что d γ / d z > 0 37. Чтобы поток Марангони доминировал, он должен быть по меньшей мере таким же быстрым, как скорость термодиффузии, V T ~ α l / δ, где α l = 0,13 × 10 -6 м 2 с -1 - коэффициент температуропроводности жидкого раствора. Этот первый критерий потока формулируется в терминах соотношения скорости Марангони, V М ~ Δγ е 0 / ηδ (из уравнения. 2), и V T. Это отношение называется числом Марангони, Ma = Δ γe 0 / ηα l, которое должно быть больше или равно 1. Второй критерий потока состоит в том, что скорость из-за тепловой плавучести,, должно быть незначительным по сравнению с V TВВ~ Д р ге20/ ηВВ~Δρграмме02/η{\ mathrm {Ra}} \ sim \ rho ge_0 ^ 2 \ delta / \ alpha _ {\ mathrm {l}} \ eta \ ll 1 T _ {\ mathrm {t}} \ lesssim T _ {\ mathrm {w}} <T _ {\ mathrm {m}} {\ mathrm {Ma}} \ gtrsim 1 {\ mathrm {Ra}} \ ll 1, в результате чего получается небольшое число Рэлея:. Приведенные выше аргументы могут быть кратко изложены как, и, где T t - температура вершины пузырька. Для замерзания пузырьков в морозильной камере все условия были выполнены при T t ≈ T w ≈ −20 ° C < T m = −6,5 ° C, Ma ≈ 13 и Ra ~ 10 - 5.R a ∼ρgе20δ/αLη≪ 1рa~ρграмме02δ/αLη«1TT≲ Tвес< TмTT≲Tвес<TмM a ≳1Ma≳1R a ≪1рa«1, Помимо генерации тепловых шлейфов, замораживание Марангони также может быть причиной того, что мы называем «эффектом снежного шара», как будет теперь обсуждаться.
Из-за большого числа Ма мы предполагаем, что потоки Марангони сдвигаются и захватывают ледяные дендриты, образующиеся на восходящем фронте замерзания. Хотя у нас нет никаких прямых доказательств того, что поток отрывается от ледяного дендрита, поскольку они слишком малы, чтобы их можно было увидеть в точке отрыва, есть два веских основания для этого утверждения. Во-первых, очень маловероятно, что сотни событий гомогенного зародышеобразования внезапно произойдут в пленке жидкости вдали от фронта замораживания, особенно если учесть, что температура в морозильной камере слишком высокая, чтобы вызвать гомогенное зародышеобразование. Это было подтверждено нанесением пузырька на сухую кремниевую пластину (все еще в морозильной камере), где никаких событий замерзания / зародышеобразования не наблюдалось даже через 30 минут (дополнительная рис. 3c).). Во-вторых, всякий раз, когда взвешенные кристаллы льда впервые появлялись (то есть увеличивались до микрометрических размеров), это всегда происходило во время потока Марангони. Действительно, рост захваченных кристаллов льда часто был сильно асимметричным из-за потока, как видно на рис. 2б, Поэтому поток Марангони должен отделять невидимо мелкие (т.е. наноразмерные) частицы льда от восходящего фронта замораживания и адвентировать их вверх. После примерно 1 с замораживания Марангони сотни микроскопических частиц льда были взвешены и росли в пленке, работая в тандеме для нагрева окружающей жидкости. В этот момент градиент температуры и поверхностного натяжения происходит во множестве мест и направлений, в отличие от первоначального случая полностью неплоского градиента, идущего от восходящего фронта замораживания. Таким образом, «эффект снежного шара» уничтожает сам поток Марангони, который создал его в первую очередь.
Этот отрыв льда можно предварительно смоделировать, уравновешивая инерцию теплового факела (F i) с силой отрыва, необходимой для раскалывания ледяного дендрита без его ледяной подложки (F трещина). Для дендритной площади контакта πl 2 сила отрыва может быть определена с использованием условия Гриффита для возникновения трещины 39
Fк р а к к= πL28 Е*весдπL-------√,FсрaсКзнак равноπL28Е*весadπL,
(3)
где w ad - произведение адгезии и. Здесь E i = 8,7 × 10 9 Па и ν i = 0,31 - модуль Юнга и коэффициент Пуассона, соответствующие льду, соответственно 40. Работа адгезии может быть количественно оценена как w ad ≈ γ i, l, где γ i, l - межфазная энергия льда относительно жидкости, определенная из соотношения Юнга, γ i, l = γ i, v - γ cos θ. Вот,Е*= Eя/ (1-ν2я)Е*знак равноЕя/(1-νя2) γ i, v ≈ 0,1 Дж м -2 - межфазная энергия льда относительно пара 41, γ ≈ 0,02 Дж м -2 (дополнительный рис. 1), а θ 0 ° - собственный краевой угол смачивания жидкого раствора. на льду. Поэтому работа адгезии между ледяным дендритом и ледяной подложкой составляет w ad ≈ 0,08 Дж / м 2. Инерция теплового шлейфа:, где v M, 0 - скорость Марангони в очень ранний срок. Экспериментально находим v M, 0Fя∼ (ρ πр2п) v2М, 0Fя~(ρπрп2)vM,02~ 10 мм с −1, взяв производную из графика δ - t (рис. 2г) при t <10 мс. Уравновешивая усилие отрыва и инерцию, F i ~ F трещина, предсказывает, что дендрит должен быть меньше чем нм для отрыва. Как показано на рис. 2, а, б, частицы увлеченного льда увеличиваются до размера ~ 100 мкм после ≈ 1 с осаждения пузырьков на ледяной подложке. Это согласуется с измеренной скоростью роста льда v i ~ 100 мкм с -1 (рис. 2дл ≲ 10L≲10), что указывает на то, что частицы льда действительно отделяются от фронта замораживания в наноразмерном размере.
Скорость роста фронта льда может быть смоделирована с помощью хорошо известной двухфазной задачи Стефана, где полубесконечная (0 < y <∞) переохлажденная жидкость с температурой T l < T m подвергается воздействию температуры T c на его границе (у = 0) в момент времени ноль. Скорость наконечника тогда определяется как
vя= 2 λ2αя/Rя,vязнак равно2λ2αя/ря,
(4)
где λ ≈ 0,03 было получено из корня трансцендентного уравнения (уравнение 5), α i = 1,15 × 10 −6 м 2 с −1 - коэффициент температуропроводности льда, а R i - радиус вершины ледяного слоя 27. Для нашего случая T c = T m трансцендентное уравнение может быть выражено как
S тLνλ e r fс (λν) e x p ((λ ν)2)= π--√,STLνλерес(λν)еИксп((λν)2)знак равноπ,
(5)
где - отношение температуропроводности льда к вода, St l = (c w (T m - T l)) / L, - удельная теплоемкость воды, а L = 334 × 10 3 Дж кг -1 - скрытая теплота плавления. Диаметр наконечника был грубо измерен как 2 R i ≈ 1,28 мкм (рис. 2f), в соответствии с предыдущим отчетом 27ν= αя/αL-----√νзнак равноαя/αLсвес= 4.2× 103JK г- 1К- 1свесзнак равно4,2×103JКграмм-1К-1и необходимость содержаться в пленке (e 0 ≈ 1,7 мкм, см. дополнительный рис. 2а). Подставляя это значение R i в формулу. 4 дает теоретическую скорость наклона v i ≈ 250 мкм с −1 (пунктирная линия на рис. 2e), что согласуется с экспериментальными измерениями роста v i ≈ 300 мкм с −1 для восходящего фронта замораживания и v i ≈ 250 мкм с −1 для кристаллов, взвешенных внутри пузырьковой пленки.