Во второй серии экспериментов пузырьки были нанесены на холодную ступень, установленную на температуру T w в окружающей среде комнатной температуры (рис. 4а). В этих условиях замораживание проходило в четыре этапа: замерзание марангони, частично замороженное равновесие, предельная регенерация и коллапс.
Рис. 4
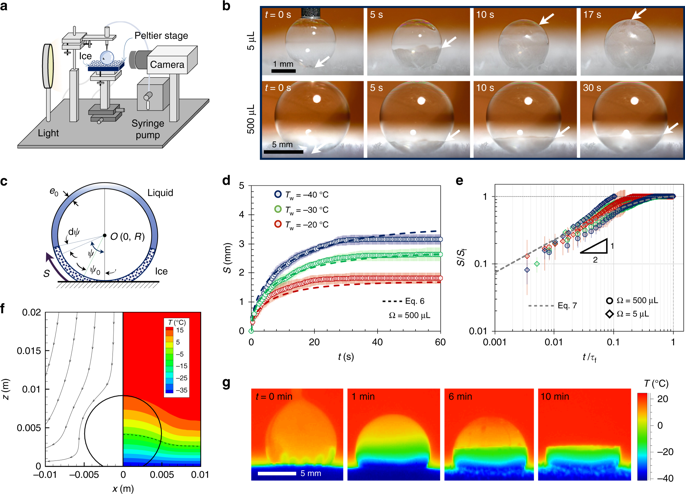
Замораживание пузырьков на холодной стадии в комнатной температуре. Схема экспериментальной установки, где пузырь контролируемого объема нанесенной на матовое подложке Пельтье с использованием шприцевой насос. b Изображение боковых изображений замерзающих пузырьков объемом Ω = 5 мкл и Ω = 500 мкл на поверхности, охлажденной при T w = −40 ± 1 ° C. Стрелки указывают развивающееся местоположение фронта замораживания, а нулевое время - это время, когда пузырь впервые осажден. c Схема, показывающая термины, используемые в формуле. 6. d Длина замороженной дуги Ω = 500 мкл пузырьков во времени. Точки данных (кружки) представляют экспериментальные данные, с погрешностями одного отклонения в трех испытаниях, в то время как пунктирные линии представляют уравнение. 6. e Как для Ω = 5 мкл (ромбы), так и для Ω = 500 мкл (кружки), построение графика замороженной длины дуги, нормализованной по конечной длине дуги (S / S f), по отношению к безразмерной шкале времени (t / τ f) привело к срыву всех данные на универсальную кривую (уравнение 7). Средние условия окружающей среды во всех экспериментах были T ∞ = 23,4 ± 1,2 ° C и относительная влажность RH = 42 ± 14%. f Моделирование профиля температуры воздуха показывает, что вблизи центра Пельтье пузырь несколько нарушил естественную конвекцию, что привело к увеличению уклона для изотемпературных линий (см. дополнительный рис. 8).). Пунктирная линия соответствует T = −6 ° C. g Термографические изображения пузырька Ω = 500 мкл, нанесенного на матовую подложку с температурой T w = −40 ± 1 ° C при комнатной температуре при T ∞ = 23,3 ± 1 ° C и относительной влажности = 23 ± 1,5%
Замораживание марангони. По аналогии с экспериментами с морозильными камерами, даже в экспериментах с комнатной температурой, мы видим, что через миллисекунды после осаждения пузырьков на охлажденной ледяной подложке происходит всплеск шлейфов Марангони, движущихся вверх от линии контакта. Разница между этими двумя экспериментами заключается в начальном положительном положительном температурном градиенте поперек пузырька в экспериментах при комнатной температуре (T t > T w). Это, однако, не влияет на начальные стадии замерзания, поскольку скрытая теплота, выделяемая в этих экспериментах для создания локальной области d T / d z <0. Однако отрицательный градиент температуры является лишь временным эффектом, так что шлейфы исчезнут в течение примерно 5 с. Возможно, из-за кратковременного характера замерзания Марангони в случае окружающей температуры при комнатной температуре «эффект снежного шара» не наблюдался. Для более крупного пузырька с Ω = 500 мкл также возможно, что наноразмерные частицы льда могли быть захвачены в потоке Марангони, но быстро расплавлены теплым верхом пузырька (T t > T m), прежде чем вырастут до микромасштабного размера.
Частично замороженное равновесие: восходящий фронт замораживания продвигался вверх по пузырю с начальной скоростью v ~ 0,1 мм с −1 (рис. 4b – e); это аналогично эквивалентной скорости фронтов затвердевания в каплях воды 42. Однако, в отличие от капель, фронт замораживания пузырька полностью остановился после (10 с) в месте, зависящем от размер пузырьков и температура подложки. За пределами этой критической шкалы времени пузыри обнаруживали состояние частично замороженного равновесия, когда верхняя часть пузыря оставалась жидкой (см. Вторую строку на рис. 4б). Единственное исключение из этой тенденции частичного замораживания было при Ω = 5 мкл и T wτе∼ Oτе~О = -40 ° C, и в этом случае пузырьки смогли полностью замерзнуть (см. Первый ряд на рис. 4b). В отличие от замерзания капель 22 снизу вверх у полностью замороженных пузырьков не было заостренного кончика, поскольку вместо этого вода может расширяться внутри полого внутреннего пространства.
Наблюдаемая тенденция неполных фронтов замерзания может быть объяснена плохой теплопроводностью длинной и тонкой мыльной пленки. Сохранение энергии в пленке пузыря может быть выражено как d T / d t = α ∇ 2 T, где α - коэффициент температуропроводности, соответствующий воде или льду. Шкала времени термодиффузии для пузырька радиуса R масштабируется как τ D ~ R 2 / α i. В противоположность этому, шкала времени движения сублимационной фронта 22, τ F ~ R / v, весы как τ е ~ τ Д л / (с я Δ Т я), где с я = 2,027 × 10 3 Дж кг -1 К -1 удельная теплоемкость льда и Δ Т я ~ 10 К разница температур типичной. Диффузии шкалы времени примерно на порядок меньше, чем морозильную шкалы времени, τ е ~ 10 τ D, что позволяет предположить, квази-устойчивый температурный профиль: ∇ 2 T = 0. Это верно для воды, так как его теплоемкости примерно в два раза выше, чем у льда.
Учитывая толщину тонкой пленки пузырьков, предполагается, что осажденный пузырь преимущественно охлаждается окружающим воздухом, а не проводимостью в подложку. Поэтому температурное поле может быть получено путем численного моделирования естественной конвекции, возникающей в воздухе над охлажденным субстратом (см. Дополнительное примечание 1). Толщина теплового пограничного слоя ζ ≈ 3 см была получена, в соответствии с экспериментальными измерениями, с использованием термопары и ступени переноса (дополнительная рис. 7). Профиль температуры воздуха слегка изменился из-за присутствия пузырька, который также был зафиксирован при моделировании (рис. 4f и дополнительные рисунки 8 и 9).
Скорость фронтов замораживания ограничена выделением скрытой теплоты плавления. Наша модель предполагает, что это скрытое тепло,, в основном сбрасывается в субстрат посредством проводимости через замороженную часть пузыря,, так как теплопроводность и градиент температуры льда намного больше, чем окружающий воздух. Жидкая верхняя часть пузыря также проводит тепло,Q˙L HQ˙LЧАСQ˙яQ˙яQ˙LQ˙Lв направлении или от фронта замораживания в зависимости от направления градиента температуры. Мы пренебрегаем конвекцией в жидкой части пузырька, так как поток Марангони обычно рассеивается к тому времени, когда фронт замораживания заметно возрастает. Этот баланс тепла в сравнении с теплом на фронте замораживания можно суммировать как, где в некоторых случаях может быть отрицательным. Для пузырька с фиксированным радиусом кривизны R эти члены могут быть полностью выражены какQ˙L H+ Q˙L= Q˙яQ˙LЧАС+Q˙Lзнак равноQ˙яQ˙LQ˙L
[ ρ L R d ψд т+ кLΔ ТLR (π- ψ)] (2πR e0s i n ψ)∼ кяΔ ТяR (ψ - ψ0)(2 πR e0s i n ψ),[ρLрdψdT+КLΔTLр(π-ψ)](2πре0sяNψ)~КяΔTяр(ψ-ψ0)(2πре0sяNψ),
(6)
где K я и к л являются теплопроводностью льда и жидкости, Δ T я и Δ Т л является температурными различиями между замороженными и незамороженными частями пузырька, ψ 0 является фиксированным угловой координатой линии соприкосновения пузыря (см Рис. 4c), а ψ - угловая координата развивающегося фронта замораживания. Небольшая разница в плотности между водой и льдом пренебрегли здесь, таким образом, что р = р л ≈ р я. Фронт замерзания всегда при температуре плавления, Т м, в то время как линия контакта всегда находится при температуре подложки, T w, что приводит к разнице температур T i = T m - T w по замерзшей части пузырька. Температура в верхней части пузырька, T t, была найдена из численного моделирования температурного поля, так что T l = T t - T m через жидкую часть пузырька. Для пузырьков объемом 5 мкл пленка жидкости имела тенденцию отводить тепло от фронта замораживания (T t < T m), в то время как тепло подводилось к фронту замораживания для пузырьков емкостью 500 мкл (T t > T m, см. дополнительную фиг. 9a).
Отмена и подобные термины, используя безразмерное время т * = т / τ е уравнение. 6 может быть безразмерным:
д ψдт*≈ β1ψ - ψ0- кLКяΔ ТLΔ Тя(β2π- ψ),dψdT*≈β1ψ-ψ0-КLКяΔTLΔTя(β2π-ψ),
(7)
где β 1 и β 2 - геометрические предварительные факторы. Как видно из рисунка 4d и дополнительного рисунка 10а, длина дуги растущего фронта замораживания, S (t) = Rψ (t), определяется уравнением. 7 для фиксированных значений β 1 = 1,8 и β 2 = 30. Следовательно, все данные сворачиваются в универсальную безразмерную кривую, как показано на рис. 4e.
Фронт замораживания перестает распространяться при d ψ / d t * → 0 при критической угловой координате ψ → ψ f (S → S f). Затем уравнение энергии упрощается до, так что ψ f можно найти какQ˙L= Q˙яQ˙Lзнак равноQ˙я
ψе= π- (π- ψ0) (β1Кяβ2КL(Δ ТяΔ ТL) +1)- 1,ψезнак равноπ-(π-ψ0)(β1Кяβ2КL(ΔTяΔTL)+1)-1,
(8)
Это также может быть выражено как критическая высота, h f = 2 R sin ((ψ f - ψ 0) / 2) (см. Дополнительную рис. 10b). Уравнение 8 представлено на рис. 5, где наклон соответствует β 1 k i / β 2 k l = 0,35. Это приводит к k i / k l = 5,83 (для тех же β 1 и β 2, что и раньше), что близко к k i / k l = 3,93, что соответствует чистой воде. Это несоответствие связано с наличием глицерина, мыльного раствора и низких температур. Возможны три различных режима замораживания: режим незамерзания, где T w ≥ T m и ψ f → ψ 0, полностью замороженный режим, где T t ≤ T m такой, что ψ f → π, и режим частично замерзания, где T t > T m > T w и ψ 0 < ψ f < π (где ψ f находится по формуле 8). Во всех объемов пузырьков и температуры поверхности, экспериментальные значения ф ф распада прекрасно на этой кривой, проверки модели. Экспериментальные измерения ф е были осложнены продолжающимся ростом иней на подложке со скоростью порядка 1 мкм с -1 (рис. 4g и дополнительные фиги. 11 и 12). Эта скорость роста мороза примерно на два порядка ниже, чем у фронта замерзания, и поэтому ее можно пренебречь, если не учитывать, что расположение h f медленно переходит наверх с нарастающими морозами.
Рис. 5
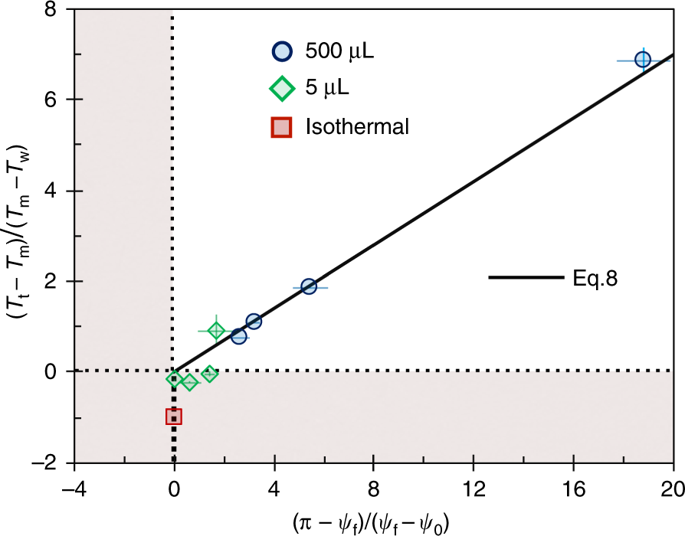
Частичное замерзание пузырьков. Критический угол, при котором фронт замораживания полностью останавливается, был найден путем уравновешивания теплопроводности через ледяную и жидкую части пузыря (уравнение 8). Изотермическое условие соответствует вертикальной пунктирной линии, где происходит полное замерзание (ψ f = π, квадратная точка данных)
Предельная регенерация: как только пузырь достиг своего частично замороженного равновесия, вначале не было заметного потока в верхней части жидкости пузырька. Примерно через 100 с произошло внезапное повторное появление шлейфов внутри жидкого купола (см. Дополнительную фиг. 5b). В отличие от плюсов, вызванных замерзанием Марангони, которые наблюдались при начальном осаждении, эти новые плюмы были обусловлены незначительной регенерацией. Конкретно, граница между льдом и жидкостью непрерывно утолщалась за счет верха жидкого купола за счет дренажа. Это было наглядно видно по появлению интерференционных полос на утончающемся жидком куполе. Шкала времени образования этих шлейфов соответствует шкале времени дренирования: t d ~ (ηR) / (ρgb 2) ~ 10 2 −10 3 с для R ~ 1–10 мм 8.
В итоге: После (10 минут) частично замороженного равновесия, жидкий купол внезапно сдулся и рухнул (рис. 6а, б). Временной масштаб от начала до конца коллапса составлял от ~ 0,1 до 10 с, в зависимости от испытания. Эта постепенная дефляция жидкого купола в течение нескольких секунд резко контрастирует с динамикой разрушения, вызванного дренажом, когда отверстие открывается и быстро расширяется (дополнительная рис. 13). Одной из возможностей коллапса является то, что постепенное охлаждение воздуха внутри пузырька приводит к снижению внутреннего давления, согласно закону Гей-Люссака 8. Однако для типичного значения температуропроводности воды / пара по отношению к воздуху α v ~ 10 −5ОО м 2 с -1, время термодиффузии τ D ~ R 2 / α v ~ 0,1 с слишком быстрое, учитывая, что жидкость остается куполообразной в течение примерно 10 мин.
Рис. 6
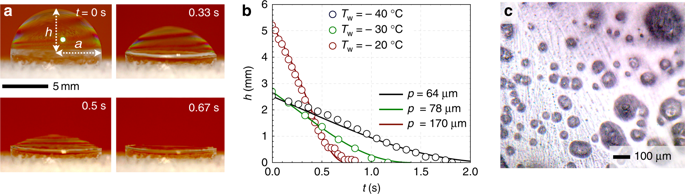
Обрушение жидкого купола частично замороженных пузырьков. a Внезапное разрушение жидкой крыши частично замороженного пузырька Ω = 500 мкл. Нулевой момент соответствует началу обрушения купола, которое завершилось за ~ 1 с. Условия были Т ш = -20 ° С, T ∞ = 24,6 ° С и относительной влажности = 58,8%. b Высота купола для жидкости (h) в зависимости от времени для разных температур подложки, для пузырьков Ω = 500 мкл. Сплошные линии соответствуют теоретической модели дренажа, представленной уравнением. 10, для наиболее подходящих значений p, показанных в легенде. с Микроскопия выявила разрывы на замерзшей части пузырька (~ 10–100 мкм), которые ответственны за постепенный отвод сжатого воздуха изнутри пузырька.
Вместо этого рассмотрим положительное давление Лапласа воздуха внутри пузырька из-за выпуклой кривизны жидкого купола. Эта разность давлений определяется как Δ P = 4 γ / r, где r = (a 2 + h 2) / 2 h - радиус кривизны жидкости, a - фиксированный радиус контакта поверхности раздела жидкость / лед, а h - высота жидкостного купола (см. рис. 6а). Если замерзшая часть пузырька содержит небольшие поры, это давление Лапласа заставит воздух вытекать из пор с динамическим давлением12ρя гv2я г12ρaярvaяр2. Следуя закону Бернулли, мы можем приравнять динамическое давление к давлению Лапласа, чтобы получить
vя г≈16γчасρя г(а2+ ч2)-----------√,vaяр≈16γчасρaяр(a2+час2),
(9)
Согласно сохранению массы, -d V s / d t ~ πp 2 v воздух, где V s = (πh / 6) (3 a 2 + h 2) - объем жидкой сферической крышки, а p - радиус поры. Если взять производную от объема по h, то изменение высоты купола жидкости по времени
д ч/ д т≈-8р2γчасρя г(а2+ ч2)3-----------√,dчас/dT≈-8п2γчасρaяр(a2+час2)3,
(10)
Плотность воздуха внутри пузырька была найдена с помощью закона идеального газа р воздуха = P / (R сек Т воздуха), где Р является абсолютным давлением, R s = 287,058 Дж кг -1 К -1 удельному газовая постоянная, а T air - это средняя температура внутри пузырька, которая была рассчитана по результатам расчетов (дополнительная рис. 9). Эти значения T air были использованы для получения ρ воздуха ≈ 1,27 кг м -3, 1,28 кг м -3 и 1,29 кг м.-3 для различных температур подложки Т ш = -20 ° С, -30 ° С и -40 ° С соответственно. Выбор значений p, которые наилучшим образом соответствуют экспериментальным данным, приводит к p ~ 10–100 мкм (рис. 6б), что согласуется с размером пористых элементов, наблюдаемых во льду (см. Рис. 6в).
Как видно из рис. 6в, возможно, что существует несколько пор, и в этом случае где N - количество пор, а p avg - это средний диаметр пор. Для небольшого числа экспериментов при комнатной температуре жидкий купол частично замороженного пузыря разорвался до того, как мог произойти коллапс, вызванный Лапласом (см. Дополнительную рис. 13). Временная шкала разрыва пузырька (~ 1 мс) намного быстрее, чем событие коллапса, обсуждаемое здесь, дополнительно демонстрируя, что механизм коллапса принципиально отличается от разрыва пленки.п2= Nп2против гп2знак равноNпavграмм2
Рисунок 7 суммирует все режимы замораживания в комплексной фазовой карте для любых возможных условий окружающей среды. Незамороженная область соответствует случаю, когда температура подложки выше, чем температура плавления мыльного раствора, что предотвращает гетерогенное зарождение восходящего фронта замораживания. Частично замороженные пузырьки возникают, когда верхняя часть пузырька теплее, чем температура плавления, а температура подложки ниже. Полностью замерзшие пузырьки наблюдаются, когда температура на поверхности и температура в верхней части пузырька субзамерзают (T t < T m и T w < T m). В этой области «эффект снежного шара» наблюдается, когда d T / d z ≤ 0 или, другими словами, T t ≤ T w (см. Диагональную линию и темно-красную область). Это условие выполняется внутри морозильной камеры, где температура подложки была равна температуре в верхней части пузырька. Обратите внимание, что из-за замерзания Марангони все виды замораживания имели тенденцию вызывать некоторую степень текучести, хотя «эффект снежного шара» имел место только в изотермическом случае.
Рис. 7
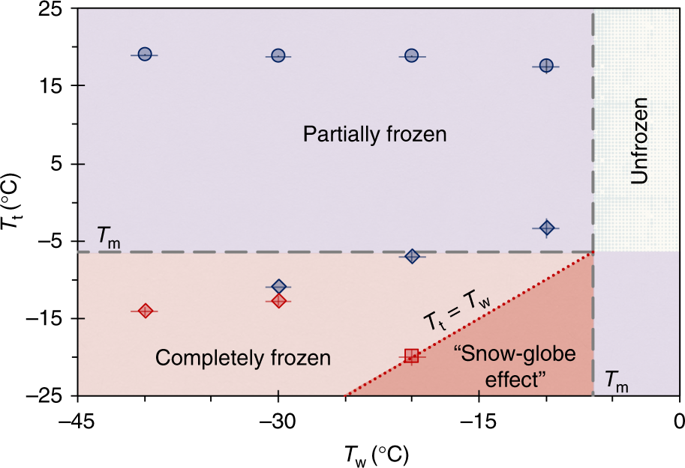
Карта режимов различных видов замерзания в мыльных пузырях. Пузыри полностью замерзают в красных областях (T t < T m и T w < T m), в то время как для замороженных пузырьков в пурпурной области возникает частично замороженное равновесие (T t > T m). Темно-красная область является подмножеством режима «Полностью заморожен», где замораживание Марангони может привести к «эффекту снежного шара» благодаря дополнительному критерию T t ≤ T w, Синие и красные точки данных соответствуют наблюдаемым в эксперименте частично замороженным или полностью замороженным пузырькам, соответственно, где объемы окружающего воздуха составляли 5 мкл (ромбы), 500 мкл (кружки) или 10 мл (квадраты). Длинные пунктирные линии соответствуют T t = T m и T w = T m, а пунктирная линия соответствует использованию изотермического морозильника
Наконец, контрольные испытания проводились с 1% -ной концентрацией чистого поверхностно-активного вещества, додецилсульфата натрия (SDS), а не с 1% мылом для посуды. Пузырьки с SDS вспыхивали в течение (10 с) при осаждении на ледяной подложке в условиях комнатной температуры (дополнительный рис. 14), скорее всего, из-за дренажа. Эти сроки осушения соответствуют предыдущему отчету 8. В течение короткого времени, когда пузырь был цел, динамика замораживания снизу вверх была эквивалентна динамике с мылом для посуды. Для изотермических условий пузырьки Ω = 500 мкл, содержащие SDS, разрываются в пределах (1 с).ОООО
Таким образом, динамика замерзания мыльных пузырей многогранна и принципиально отличается от классически изученного сценария замораживания объемных объемов жидкости. В охлажденных и изотермических условиях сотни частиц льда отделяются от фронта замерзания и закручиваются вокруг пузыря в «эффекте снежного шара». Этот красивый танец был вызван локальным подводом скрытой жары на фронте замораживания, что вызвало сильный поток Марангони, способный откалывать мелкие кристаллы льда. Поэтому изотермические пузырьки очень эффективно замерзают из-за сотен фронтов, растущих в тандеме и сцепляющихся вместе. Когда пузырьки замораживаются на холодной стадии в среде с комнатной температурой, фронт замораживания медленно распространяется вверх и полностью останавливается на критической высоте. Было обнаружено, что динамика фронта замораживания улавливается проблемой Стефана, определяемой балансом между скрытой теплотой и проводимостью по замороженным и незамерзшим частям пузырька. После остановки фронта замораживания частично замерзший пузырь остается в равновесии в течение многих минут, после чего происходит дефляция и коллапс жидкого купола из-за его давления Лапласа, проталкивающего воздух через небольшие поры во льду. Эти результаты показывают, что динамика замерзания жидкости в значительной степени зависит от ее геометрических условий, и что большое разнообразие многофазных явлений происходит, когда объем жидкости не является ни непрерывным, ни поверхностным. с последующим спадом и обвалом жидкого купола, из-за его давления Лапласа, выталкивающего воздух через небольшие поры во льду. Эти результаты показывают, что динамика замерзания жидкости в значительной степени зависит от ее геометрических условий, и что большое разнообразие многофазных явлений происходит, когда объем жидкости не является ни непрерывным, ни поверхностным. с последующим спадом и обвалом жидкого купола, из-за его давления Лапласа, выталкивающего воздух через небольшие поры во льду. Эти результаты показывают, что динамика замерзания жидкости в значительной степени зависит от ее геометрических условий, и что большое разнообразие многофазных явлений происходит, когда объем жидкости не является ни непрерывным, ни поверхностным.
Методы
Материалы
Мыльные пузыри были получены с использованием раствора, состоящего из 79% (по объему) дистиллированной воды, 20% глицерина (Sigma-Aldrich, 56-81-5) и ≈1% мыла для посуды (Palmolive ®, Ultra AntiBacterial Dish Liquid). Мыло для посуды состоит из 98% инертных ингредиентов (вода, лауретсульфат натрия, лаурамидопропилбетаин, додецилбензолсульфонат натрия, спирт SD 3 A, ксилолсульфонат натрия, ароматизатор, тетранатриевая соль ЭДТА и красители) и 2% активного ингредиента (L-молочная кислота). кислота). Для контрольных экспериментов вместо мыла для посуды использовали додецилсульфат натрия (Sigma-Aldrich, 75746). После перемешивания смеси ее оставляли на ночь перед проведением любых экспериментов. Пренебрегая эффектами мыла, ранее сообщалось о температуре замерзания смеси воды и глицерина 80–20% 29быть T m ≈ −6,5 ° C.
Для экспериментов при комнатной температуре пузырьки осаждали на матовой стадии Пельтье (Раме-Харт, модель 100-30) с использованием шприцевого насоса (Раме-Харт, модель 100-22). Использовали иглу с внутренним и внешним диаметрами 0,7 мм и 2,1 мм соответственно. Эксперименты были записаны с использованием камеры DSLR (Canon ®, EOS 5D Mark III) с макрообъективом (Canon MP-E 65 мм f / 2,8 1–5 ×). После замораживания поры и / или пузырьки, попавшие в лед, были охарактеризованы с использованием нисходящего оптического микроскопа (Nikon 150LV) с линзой с большим рабочим расстоянием (Mitutuyo, MPlan APO).
Для изотермических экспериментов полистироловую чашку Петри (VWR, 25384-326) наполняли дистиллированной водой и оставляли в морозильной камере (Frigidaire, модель FRT21IL6JB2) с температурой -20 ° C в течение ночи. Ледяные диски хранили в холодильнике (Igloo ®) при транспортировке в морозильную камеру (Conviron, модель C1008). Ледяной диск оставляли в морозильной камере в течение по крайней мере часа перед началом экспериментов, чтобы гарантировать, что его температура соответствует температуре воздуха. В некоторых контрольных экспериментах пузырьки наносились на сухую кремниевую подложку, а не на ледяной диск. Эксперименты были записаны с использованием высокоскоростной камеры (Vision Research, Phantom v711). Относительная влажность и температура воздуха в морозильной камере измерялись гигрометром (E + E Elektronik, модель EE210). Тепловизионные эксперименты проводились с использованием ИК-камеры (FLIR SC655).
Осветительные приборы
Для экспериментов при комнатной температуре для переднего освещения использовался прожектор (Advanced Illumination, модель SL164), а для подсветки использовался квадратный светодиод (Advanced Illumination, модель BX0808). При изображении замороженного пузырька с помощью микроскопа сверху вниз использовалось светодиодное освещение для минимизации эффектов нагрева (Nikon, LV-UEPI Universal Epi Illuminator 2). Для изотермических экспериментов круглый светодиод (Genaray, модель SP-AD75) был помещен под ледяной диск с горизонтальной ориентацией, чтобы осветить пузырь (см. Дополнительную рис. 3а). Перья (рис. 3 и дополнительный рис. 5а) были визуализированы с использованием света LOWEL DP, который находился на расстоянии около 5 м от экспериментальной установки, чтобы минимизировать эффекты нагрева.
Обработка изображений
Видео были импортированы в программное обеспечение с открытым исходным кодом (Tracker), чтобы отслеживать три точки (крайний левый, крайний правый и центральный) замерзающих пузырьков. Система координат была размещена так, что ось y пересекала центр пузырька, а ось x была расположена на линии контакта границы раздела пузырь / подложка. Окончательный угол, при котором фронт замораживания перестал распространяться, был найден путем импорта соответствующего изображения в ImageJ.
Доступность данных
Данные, подтверждающие результаты этого исследования, доступны в статье и связанных с ней дополнительных материалах. Любые другие данные доступны от соответствующего автора по запросу.
Ссылки
Смотри в статье. Их там ещё столько же сколько тут текста